单选题1：执行下面代码输出（）。

s = '123'print(s + s)

（A）246

（B）123123

（C）123

  (D)  s+s

（E）123 + 123

答案：B

单选题2：执行下面代码可能输出（）。

import random as rprint(r.randrange(2, 30, 2))

（A）  1

（B）  4

（C）  11

（D）  25

（E）  30

答案：B  注：含头不含尾的偶数。

单选题3：执行下面代码输出（）。

data = {101.3,234,58,2}print(type(sorted(data)))

（A）  <class 'float'>

（B）  <class 'set'>

（C）  <class 'int'>

（D）  <class 'str'>

（E）  <class 'list'>

答案：E  注：sorted返回集合的列表副本。

单选题4：下面代码能正确运行，得到整数结果的是（）。

（A）  a = 1 + map('1')

（B）  a = 1 + str('1')

（C）  a = 1 + int('1')

（D）  a = 1 + float('1')

（E）  a = 1 +list('1')

答案：C  注：D也可以运行但得到的是浮点数。

单选题5：Python支持数学中的复数，描述错误的是（）。

（A）  复数由实部与虚部构成。

（B）  复数可以看作2个有序的浮点数系列(a,b)

（C）  实部和虚部都是浮点数

（D）  虚数部分需要加“j”或“J”后缀

（E）  从已知复数f中获得虚数部分，可以使用f.real

答案：E  注：也许没有复数的概念，但从题中可知复数有2部分——实部与虚部，real是“实”，不可能是虚数部分。

编程题1：

　　输入一个整数n，输出n + n的值。

样例输入：5

样例输出：10

解答：

n = int(input())print(n+n)

编程题2：

　　输入一个只含有大写字母的字符串s（长度超过2），按顺序输出这个字符串的头尾2个字母，中间不留空格或有其它字符。

输入样例：XYZ

输出样例：XZ

解答：

s = input()print(s[0]+s[-1])

编程题3：

　　质数是符号以下条件的正整数：除了1和它本身能整除它外，没有别的正整数能整除它。除了1和质数外的正整数是合数。换一句话说，除了1和本身能整除它外，还有别的正整数能整除它。例如6，除了能被1和6整除外，还能被2和3整除。

　　小黄有一些硬币，数量（n）不少于2个，不超过25个，每个硬币都有一个正整数的面值（可能相同）。从这些硬币中选出（p）不少于2个，不超过n个的硬币，选法可能不唯一。请帮小黄解决下面2个问题：

1、硬币面值累加和中有多少个不同的值；

2、硬币面值累加和中有多少个不同的合数。

　　例如：n = 4, p =2, 4个硬币的面值分别是1,5,4,2，有6中选法，它们的面值累加：1+5=6；1+4=5；1+2=3；5+4=9；5+2=7；4+2=6 。有5个不同的累加值：6,5,3,9,7；2个不同的合数：6,9。

输入描述：

第一行输入硬币的个数，一个正整数n（2≤n≤25）。

第二行输入硬币面值，n个正整数，以英文逗号隔开。

第三行输入选取硬币的数量p（2≤p≤n）。

输出描述：

输出累加和不同值的个数和累加和不同值的合数个数，用英文逗号分隔。

输入样例：

4

1,5,4,2

2

输出样例：

5,2

解答：

n = int(input())nums = list(map(int, input().split(',')))p = int(input())#构建全部集合all = set()def plus(ns,rst):    if len(rst) == p:        all.add(sum(rst))        rst.clear()    if len(ns) + len(rst) < p:        return    for i in range(len(ns)):        ns1 = ns.copy()        rst1 = rst.copy()        rst1.append(ns1.pop(i))         plus(ns1,rst1)​plus(nums,[])​#合数个数hs = 0def checkPN(pn):    for i in range(2,pn//2+1):        if pn % i == 0:            return 1    return 0for it in all:    hs += checkPN(it)​rst = [str(len(all)),str(hs)]​print(",".join(rst))

方法要点：这是一个组合问题，及质数与合数的概念问题。

解题思路：

　　为了能使没学过组合数学知识的人能理解，本解法采用手动组合：集合中抽出一个元素与剩下的元素组合，如此类推。Python列表的实现方法是：浅拷贝原列表list.copy()，然后list.pop(i)一个元素放入浅拷贝的结果列表中，用剩下的列表和这个浅拷贝的结果列表递归调用。质数与合数问题是老生常谈，这里就略了。

编程题4：

　　把二项式(a + b)^n展开式的的系数按（n = 0, 1, 2, 3, ……）逐行左右对称扩张排列，构成了一个三角形。我们把这个三角形叫做杨辉三角形，因为杨辉发现了下面两个规律：

（1）首尾2数都是1，其它数是左上方和右上方的数之和；

（2）第N（N=n+1）行有N个数。

　　为了研究杨辉三角形，我们也引入了“列”的概念。就是杨辉三角形行的元素下标相同，在等腰三角形的杨辉三角形中，是斜的。

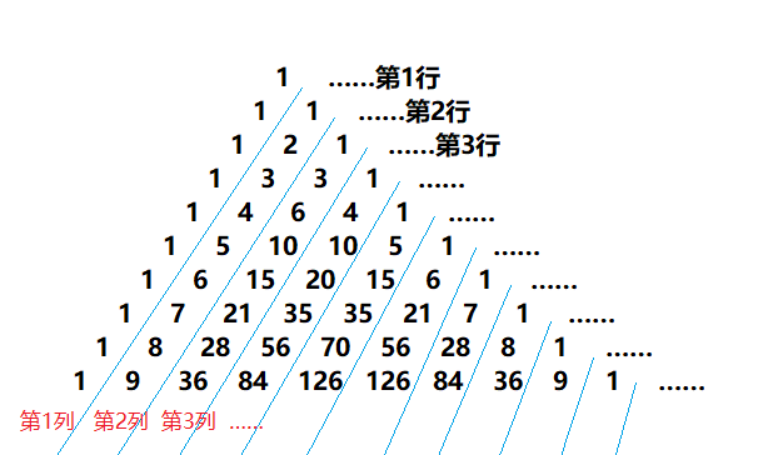
　　编程解决下面两个问题：

（1）求第A行第B列对应的数值；

（2）求N行杨辉三角形中B列所有值之和。

例如：N=6，6行的杨辉三角形如下图：

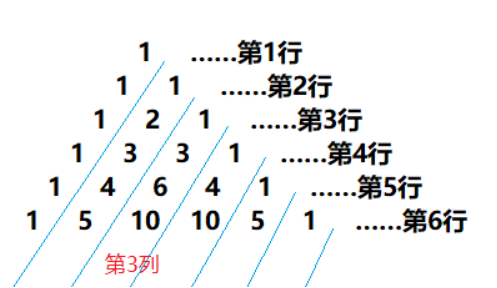
N=6，A=6，B=3，第6行第3列的值是10；第3列所有值之和20（=10+6+3+1）。

输入描述：

第一行输入杨辉三角形的行数N（从1开始算，2≤N≤30）

第二行输入两个正整数A和B（1≤B≤A≤N）用英文逗号隔开，分别表示第A行和第B列。

输出描述：

输出用英文逗号隔开的两个整数，分别表示N行杨辉三角形中的第A行B列的数和第B列数之和。

输入样例：

6

6,3

输出样例：

10,20

解答：

N = int(input())A, B = map(int, input().split(','))#N行的杨辉三角形，用直角的杨辉三角形问题就非常明显line = [1]yh = [line]for i in range(1,N):    temp = [1]    for j in range(1,len(line)):        temp.append(line[j]+line[j-1])    temp.append(1)    yh.append(temp)    line=tempxyv = yh[A-1][B-1]ycv = 0for i in range(B-1,N):    ycv += yh[i][B-1]​rst = str(xyv), str(ycv)​print(",".join(rst))​

方法要点：把杨辉三角形画成直角的，问题迎刃而解。

解题思路：

　　把杨辉三角形画成直角的，因此可以认为杨辉三角形是切去右上角的（对角线除外）的矩阵（当然也可以用0补全为矩阵），所谓的行列，就是这个矩阵的行列了。

编程题5：

　　在一面墙上，有n列边长为1的正方形瓷砖贴在上面（1≤n≤106），每列瓷砖的数量p（1≤p≤104，相邻列之间不留空隙）。现想在最大的矩形的瓷砖上画上壁画，小明目测一下很快就指出这个矩形，但别人不相信，请编程找出这个最大的矩形，证明小明的目测是否正确。

　　例如：n=6，即有6列瓷砖贴在墙上，每列瓷砖的数量依次为2,3,1,6,5,2，如下图：

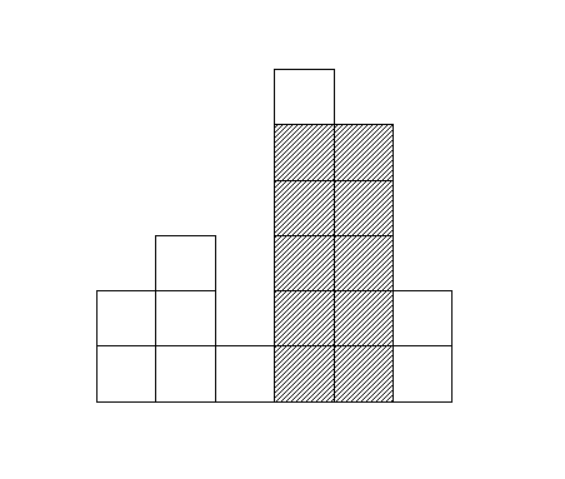
图中矩形（阴影部分）面积最大，是10。

输入描述：

第一行输入瓷砖的列数n（正整数，1≤n≤106）

第二行输入n瓷砖的数量p（正整数，1≤p≤104，用空格隔开）

输出描述：

最大的矩形面积（正整数）

输入样例：

6

2 3 1 6 5 2

输出样例：

10

解答：

n = int(input())nums = list(map(int,input().split()))#构建01矩阵maxHigh = max(nums)mx = []for i in range(n):    mx.append([1]*nums[i]+[0]*(maxHigh-nums[i]))​minHigh = min(nums)#最大面积maxA = minHigh * n#分层统计for i in range(minHigh,maxHigh):    s = 0    j = 0    while j < n:        while j < n and mx[j][i] == 0:  #定位到非0            j += 1        while j < n and mx[j][i] > 0:  #连续块            s += 1            j += 1        if s > 0:            tmp = s * (i+1)  #矩形面积            if tmp > maxA:                maxA = tmp            s = 0​print(maxA)​

方法要点：把问题转化为01矩阵问题；后续的层连续是1，它前面的层对应的列一定是连续的1。

解题思路：

　　把列瓷砖变为一行瓷砖，然后补齐虚瓷砖数量，这个问题就转化为只含0和1的矩阵。用一个主循环按层统计，主循环中含两个循环，第一个用于定位开始的1，第二个循环用于统计连续1的个数，从而计算矩形面积。

编程题6：

　　在太空中有N个神奇的宇宙飞船（编号从1到N），每个飞船都可能有1个或多个时光隧道，每个时光隧道都有一个编号，在同一个飞船中，时光隧道的编号不重复，同一个时光隧道编号可能出现在多个飞船中，如果不同的飞船有编号相同的时光隧道就可以互通。

　　某宇航员要从X编号的飞船到Y编号的飞船，他至少需要经过几个飞船（出发飞船不算）。

例如：N=4，4个飞船的时光隧道编号分别为：

飞船1：A、C、F、G

飞船2：B、C、D、E

飞船3：D、P、Q

飞船4：Q、D、C

其中，飞船1、飞船2和飞船4互通，共用C时光隧道；飞船2与飞船3互通，共用D时光隧道；飞船2与飞船4互通，共用C、D时光隧道；飞船3与飞船4互通，共用D、Q时光隧道。

当X=1，Y=2，从飞船1到飞船2共有三种路线：

路线1：从飞船1通过时光隧道C到达飞船2，共经过1个时光隧道；

线路2：从飞船1通过时光隧道C到达飞船4，再通过时光隧道C或D到达飞船2，共经过2个时光隧道；

路线3：从飞船1通过时光隧道C到达飞船4，再通过时光隧道D或Q到达飞船3，再通过时光隧道D到达飞船2，共经过3个时光隧道；

所以从飞船1到飞船2至少要经过1个时光隧道。

输入描述：

第一行输入飞船数n（正整数，2≤n≤20）

然后输入n行时光隧道编号（不含英文逗号字符串，用英文逗号分隔）

最后一行输入出发飞船和到达飞船的编号（两个正整数，英文逗号隔开）

输出描述：

从飞船X到达飞船Y最少经过的时光隧道数（整数，如果无法到达则是-1）

输入样例1：

4

A,C,F,G

B,C,D,E

D,P,Q

Q,D,C

1,2

输出样例1：

1

输入样例2：

4

A,C,F,G

B,D,E

D,P,Q

Q,D,C

1,2

输出样例2：

2

解答：

N = int(input())rooms = [set(input().split(',')) for i in range(N)]X, Y = map(int, input().split(','))X, Y = X-1, Y-1​def checkLink(lst, tar):    for r in lst:        if len(r & tar) > 0: #与其中一个相连            return True    return False​rX = rooms[X]rY = rooms[Y]if len(rX & rY) > 0: #X，Y直通    minR = 1else:    minR = -1    sm = 0     #分层统计    lst1 = [rX]    rooms.remove(rX)    rooms.remove(rY)    lst2 = rooms    while len(lst1)>0 and len(lst2)>0:        sm += 1        hasFound = False        tmpLst1 = []        tmpLst2 = []        for r in lst2:            if checkLink(lst1,r):                if len(r & rY) > 0: #通Y                    sm += 1                    hasFound = True                    break                else:                    tmpLst1.append(r) #压入下层            else:                tmpLst2.append(r)​        if hasFound:            minR = sm            break        lst1=tmpLst1        lst2=tmpLst2  #下一层​print(minR)​

方法要点：有向图的分层遍历、集合的“与”运算。

解题思路：

　　从题中可得到这是一个“图”。但是，我们仔细想一想，对于求从X节点到Y节点的最短路径，因此图中的回环是没有意义的。于是这个问题就可以转化为“有向图”求最短路径问题。本文采用有向图的分层遍历法求解。

后语：

　　由于时间比较仓促，不免有错漏，请指正；另外如果无法看懂代码，请留意询问或加微信13729135043。

附录：蓝桥杯大赛青少组 第十四届蓝桥杯Python真题答案

单选题1：

答案：A

单选题2：

答案：A  注：含头不含尾的偶数。

单选题3：

答案：D  注：sorted返回集合的列表副本。

单选题4：

答案：B

单选题5：

答案：D  注：real是“实”，不可能是虚数部分。

编程题1：

解答：

N = int(input())print(N+N)

编程题2：

解答：

s = input()print(s[0]+s[-1])

编程题3：

解答：

N = int(input())nums = list(map(int, input().split(',')))K = int(input())#构建全部集合all = set()def plus(ns,rst):    if len(rst) == K:        all.add(sum(rst))        rst.clear()    if len(ns) +len(rst)< K:        return    for i in range(len(ns)):        ns1 = ns.copy()        rst1 = rst.copy()        rst1.append(ns1.pop(i))         plus(ns1,rst1)​plus(nums,[])​#合数个数hs = 0def checkPN(pn):    for i in range(2,pn//2+1):        if pn % i == 0:            return 1    return 0for it in all:    hs += checkPN(it)    rst = [str(len(all)),str(hs)]​print(",".join(rst))​

编程题4：解答：

N = int(input())X, Y = map(int, input().split(','))#N行的杨辉三角形，用直角的杨辉三角形问题就非常明显line = [1]yh = [line]for i in range(1,N):    temp = [1]    for j in range(1,len(line)):        temp.append(line[j]+line[j-1])    temp.append(1)    yh.append(temp)    line=tempxyv = yh[X-1][Y-1]ycv = 0for i in range(Y-1,N):    ycv += yh[i][Y-1]​rst = str(xyv), str(ycv)​print(",".join(rst))​

编程题5：

解答：

N = int(input())nums = list(map(int,input().split()))#构建01矩阵maxHigh = max(nums)mx = []for i in range(N):    mx.append([1]*nums[i]+[0]*(maxHigh-nums[i]))​minHigh = min(nums)#最大面积maxA = minHigh * N#分层统计for i in range(minHigh,maxHigh):    s = 0    j = 0    while j < N:        while j < N and mx[j][i] == 0:  #定位到非0            j += 1        while j < N and mx[j][i] > 0:  #连续块            s += 1            j += 1        if s > 0:            tmp = s * (i+1)  #矩形面积            if tmp > maxA:                maxA = tmp            s = 0            print(maxA)        ​

编程题6：解答：

N = int(input())rooms = [set(input().split(',')) for i in range(N)]A, B = map(int, input().split(','))A, B = A-1, B-1​def checkLink(lst, tar):    for r in lst:        if len(r & tar) > 0: #与其中一个相连            return True    return False​rA = rooms[A]rB = rooms[B]if len(rA & rB) > 0: #A，B直通    minR = 1else:    minR = -1    sm = 0     #分层统计    lst1 = [rA]    rooms.remove(rA)    rooms.remove(rB)    lst2 = rooms    while len(lst1)>0 and len(lst2)>0:        sm += 1        hasFound = False        tmpLst1 = []        tmpLst2 = []        for r in lst2:            if checkLink(lst1,r):                if len(r & rB) > 0: #通B                    sm += 1                    hasFound = True                    break                else:                    tmpLst1.append(r) #压入下层            else:                tmpLst2.append(r)                            if hasFound:            minR = sm            break        lst1=tmpLst1        lst2=tmpLst2  #下一层​print(minR)            

​