一、选择题
第一题执行print("{1}{0}".format("Hello","Python","!"))语句后,输出的结果是( )。A、HelloPython! B、PythonHello! C、HelloPython D、PythonHello答案:D
解说:{}中的数字是format参数的下标(从0开始)。
第二题下列函数中哪一个可以删除集合中指定的元素?( )A、clear() B、discard() C、union() D、issubset()答案:B
解说:clear()删除所有元素,例如:
·
·
·
·
aset = set([1,2,3,4,4,5])print(aset)aset.clear()print(aset)
运行结果:
·
·
{1, 2, 3, 4, 5}set()
union()是合集,例如:
·
·
·
·
·
·
·
·
·
aset = set([1,2,3,4,4,5])bset = set([4,5,6,7])print(aset)print(bset)cset = aset.union(bset)print("运算后:")print(aset)print(bset)print(cset)
运行结果:
·
·
·
·
·
·
{1, 2, 3, 4, 5}{4, 5, 6, 7}运算后:{1, 2, 3, 4, 5} {4, 5, 6, 7}{1, 2, 3, 4, 5, 6, 7}
issubset()判断当前集合是否为参数集合的子集,例如:
·
·
·
·
·
·
·
aset = set([1,2,3,4,4,5])bset = set([4,5,6,7])cset = aset.union(bset)print(aset.issubset(cset))print(bset.issubset(cset))print(cset.issubset(aset))print(cset.issubset(bset))
运行结果:
·
·
·
·
TrueTrueFalseFalse
discard()删除集合中指定(参数)元素,例如:
·
·
·
·
aset = set([1,2,3,4,4,5])print(aset)aset.discard(4)print(aset)
运行结果:
·
·
{1, 2, 3, 4, 5}{1, 2, 3, 5}
第三题
以下选项中,哪一个可以将字典dict1与字典dict2合并?( )A、dict1.add(dict2) B、dict1.extend(dict2) C、dict1.update(dict2) D、dict1.merge(dict2)答案:C解说: dict1.update(dict2)代码样例:
·
·
·
·
·
·
·
dict1 = {1:"A",2:"B"}dict2 = {2:"C",3:"D"}print(dict1)print(dict2)dict1.update(dict2)print(dict1)print(dict2)
运行结果:
·
·
·
·
{1: 'A', 2: 'B'}{2: 'C', 3: 'D'}{1: 'A', 2: 'C', 3: 'D'}{2: 'C', 3: 'D'}
add(item)是集合增加一个元素的方法,样例如下
·
·
·
aset = set([1,2,3])aset.add(10)print(aset)
运行结果:
·
{10, 1, 2, 3}
extend(list2)是列表接上另一个列表,样例如下
·
·
·
·
·
list1 = [1,2,3]list2 = [3,4,5]list1.extend(list2)print(list1)print(list2)
运行结果:
·
·
[1, 2, 3, 3, 4, 5][3, 4, 5]
merge是表格合并函数(panda模块中),请查阅有关资料。
第四题关于Python中的全局变量和局部变量,以下选项描述错误的是( )。A、全局变量不可以被函数内部的代码块修改B、全局变量在函数之外一般没有缩进,在程序执行全过程有效C、全局变量是指在函数之外定义的变量,而局部变量是指在函数内部定义的变量D、局部变量和全局变量可以共存,但如果局部变量和全局变量的名称相同,局部变量会覆盖全局变量答案:A解说:全局变量在函数内部用global标识后可以修改,其他都正确。
第五题以下选项中,哪一个可以更好地描述Python中类方法和静态方法之间的区别?( )A、类方法只能由类调用,而静态方法只能由实例调用B、类方法可以访问类和实例的属性和方法,而静态方法不能访问C、类方法必须将类作为第一个参数,二静态方法可以没有参数D、类方法只能访问类的属性和方法,而静态方法只能访问实例的属性和方法。答案:C解说:
类中的方法分为3类:
1. 实例方法 instance method
不使用装饰器
类中的所有方法,如果第一个参数是 self,就是 instance method, self 是创建的类实例,实例方法与实例即对象相关。
(self 可以改成别的名称,但使用 self 是convention,self 是类实例, ),
2. 类方法 class method
使用 @classmethod 装饰
类方法的第一个参数总是 cls。如果方法需要类的信息,用 @classmethod 对其进行装饰, 类方法经常被用作 factory,例如如下代码中的 hardcover 和 paperback 两个 class method 方法就是可用于创建对象的 factory。
(cls 可以改成别的名称,但使用 cls 是convention)
3. 静态方法 static method
使用 @staticmethod 装饰
静态方法并不是真正意义上的类方法,它只是一个被放到类里的函数而已。
尽管如此,仍然称之为方法,但它没有关于 class 或 object 的任何信息,所以它实际上是一个独立的函数,只是被放到了类里,静态方法既没有 self 也没有 cls 参数 。(静态方法可以访问类属性,例如 Book.TYPES)
静态方法通常用于组织代码,例如如果认为将某个函数放到某个类里,整体代码会因此更符合逻辑,于是可以将这个函数变成该类的静态方法。所以如果需要在类里放一个函数进去,此函数不会用到任何关于类或实例的信息,那么就可以用 @staticmethod 对其进行装饰。
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
class Book: TYPES = ("hardcover", "paperback") # 精装,平装 def __init__(self, name, book_type, weight): self.name = name self.book_type = book_type self.weight = weight def __repr__(self): return f"<Book {self.name}, {self.book_type}, weighing {self.weight}g>" def instance_method(self): print(f"Called instance method of {self}") @classmethod def class_method(cls): print(f"called class method of {cls}") @classmethod def hardcover(cls, name, paper_weight): # cls 名称任意,使用 cls 是 convention # 下一行的cls,改成 Book,代码也能跑,但应该写成 cls, 以避免在 inheritance 可能会遇到的问题 return cls(name, cls.TYPES[0], paper_weight + 100) # @classmethod def paperback(cls, name, paper_weight): # 下一行的cls,改成 Book,代码也能跑,但应该写成 cls, 以避免在 inheritance 可能会遇到的问题 return cls(name, cls.TYPES[1], paper_weight) @staticmethod def static_method(): print("Called static method")book = Book("Dive into Python", Book.TYPES[1], 800)# Called instance method of <Book Dive into Python, paperback, weighing 800g>book.instance_method() # 下一行代码和上一行完全等价# Called instance method of <Book Dive into Python, paperback, weighing 800g>Book.instance_method(book) # called class method of <class '__main__.Book'>Book.class_method()# Called static methodBook.static_method()h_book = Book.hardcover("Harry Potter", 1500)light = Book.paperback("Python 101", 600)# <Book Harry Potter, hardcover, weighing 1600g>print(h_book)# <Book Python 101, paperback, weighing 600g>print(light)
二、编程题第一题编程实现:给定一个字符串S(S长度<100),统计字符串中字母一共有多少个。例如:S = "1Abb",其中字母有A,b,b一共有3个。
输入描述:输入一个字符串S(S长度<100)
输出描述:输出一个整数,表示字符串S中的字母的个数样例输入:1Abb
样例输出:3
代码:
·
·
·
·
·
·
·
S = input()iA, iZ, ia, iz = ord('A'), ord('Z'), ord('a'), ord('z')count = 0for i in map(ord, S): if iA<=i<=iZ or ia<=i<=iz: count += 1print(count)
解说:
用ASCII码范围判断,str.isalpha方法不是很恰当,因为它把汉字也认为是字母,下面的代码:
·
·
·
·
·
·
S = '4aD好'count = 0for ch in S: if ch.isalpha(): count += 1print(count)
运行结果是:3。
第二题提示信息:
有一个有多个小正六边形组成的蜂巢图案,蜂巢外缘各边的小正六边形数量一致,且左右对称。
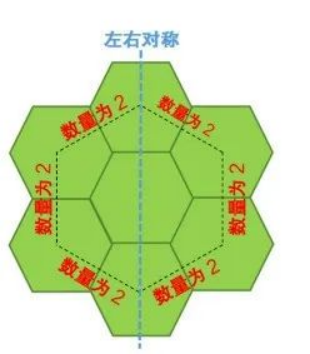
(上图蜂巢图案外缘各边小正六边形数量为2)以下为竖直对称线上小正六边形个数为3、5、7的3个蜂巢图案。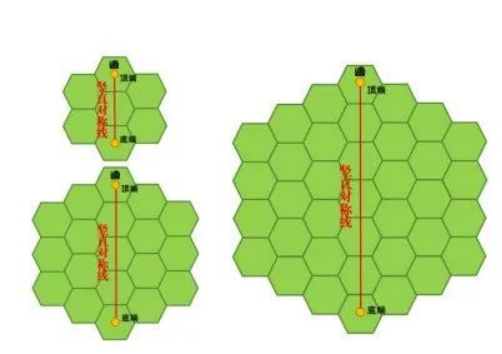 编程实现:
编程实现:
有一只蜗牛要从竖直对称线顶端的小正六边形处移动到底端的小正六边形中,它每次只能向它所在的位置的小正六边形的左下方、正下方、右下方相邻的小正六边形移动。
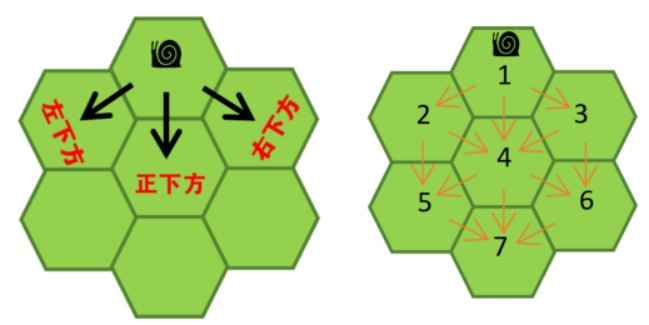
已知竖直对称线上有N个小正六边形,请计算出蜗牛从竖直对称线顶端移动到底端共有多少条不同的移动路线。例如:N = 3,竖直对称线上有3个小正六边形,如下图:

蜗牛从竖直对称线顶端的小正六边形(1号处)移动到另一端的小正六边形中(7号处)共有11条不同的路线。
11条不同的路线分别为:
(1->2->5->7)、(1->2->4->7)、(1->2->4->5->7)、(1->2->4->6->7)、(1->4->5->7)、(1->4->7)、(1->4->6->7)、(1->3->4->5->7)、(1->3->4->7)、(1->3->4->6->7)、(1->3->4->7)。
输入描述:输入一个正整数N(2<N<30,N为奇数),表示图案上竖直对称线上小正六边形的个数
输出描述:输出一个整数,表示蜗牛从竖直对称线顶端移动到底端共有多少条不同的移动路线
样例输入:3
样例输出:11
递归代码:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
N = int(input())count = 0 #方案数 #递归移动def move(row,col): global count if row == N - 1 and col == 0: #到达终点 count += 1 return if col < -(N-1)//2 or col > (N-1)//2 or abs(col)+row > N -1: #越界 return #左下移 move(row + 1 if col > 0 else row, col - 1) #递归调用 #正下移 move(row + 1, col) #右下移 move(row + 1 if col < 0 else row, col + 1)
move(0,0)print(count)
循环代码:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
N = int(input())count = 0 #方案数 #循环移动lst1 = [(0,0)]lst2 = []while len(lst1) > 0: for row, col in lst1: if row == N - 1 and col == 0: #到达终点 count += 1 continue if col < -(N-1)//2 or col > (N-1)//2 or abs(col)+row > N -1: #越界 continue #左下移 lst2.append((row + 1 if col > 0 else row, col - 1)) #正下移 lst2.append((row + 1, col)) #右下移 lst2.append((row + 1 if col < 0 else row, col + 1))
lst1 = lst2 lst2 = []
print(count)
解说:

如上图,任一竖直的列把蜂巢分为左右两部分,每一行都是一条折线,折点是这条竖直的列,左点向下和向右都进入下一行,右点向下和向左也都进入下一行,竖直列上的一点只有向下才进入下一行。 从0开始向下进行行编号(0,1,2,...),左边的列为负,右边的列为正,这就是蜂巢平面的坐标系。很自然就得到移到的方法:
·
·
·
·
·
·
#左下移move(row + 1 if col > 0 else row, col - 1) #递归调用#正下移move(row + 1, col)#右下移move(row + 1 if col < 0 else row, col + 1)
加入到达终点的代码:
·
·
·
·
global count if row == N - 1 and col == 0: #到达终点 count += 1 return
左右越界容易得到,关键是左下和右下的越界。通过对坐标的观察容易得到,左下和右下的边界的行列坐标的绝对值之和是恒定的,从而得到越界代码:
·
·
·
if col < -(N-1)//2 or col > (N-1)//2 or abs(col)+row > N -1: #越界 return
第三题编程实现:
某公司有多间会议室,可使用时间为8点到22点,同一会议室同一时间段只能由一个部分使用。
一天有N(1≤N≤50)个部门计划使用同一间会议室,且已知每个部门计划使用开始时间S(8≤S≤21)和结束时间E(S≤E≤22)。例如:N = 3,3个部门计划使用的开始及结束时间依次为(9, 12),(10, 15),(15, 20)。

10~12点的时段,部门1和部门2都计划使用,所以只能由一个部门使用;15~20点的时间段,只有部门3计划使用,所以这间会议室最多可以安排2个部门使用(部门1和部门3或者部门2和部门3)。
输入描述:
第一行输入一个正整数N(1≤N≤50),表示计划使用同一间会议室的部门数量。第二行开始,输入N行,每行两个正整数S和E(8≤S≤21,S≤E≤22),分别表示某个部门计划使用会议室的开始时间和结束时间,正整数之间以一个空格隔开。
输出描述:
输出一个整数,表示这间会议室最多可以安排多少个部门使用。
样例输入:
3
9 1210 15
15 20样例输出:
2
代码:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
N = int(input()) # 部门数量class PartNode(): #部门节点 def __init__(self, S, E): #开始、结束 self.S = S self.E = E self.sublst = [] #冲突部门列表parts = [] # 部门对象列表for i in range(N): S, E = map(int, input().split()) parts.append(PartNode(S, E)) #初始化重叠数量parts.sort(key=lambda x : x.S) #按开始时间排序for i in range(N-1): for j in range(i+1, N): if parts[j].S < parts[i].E: #如果后续的部门的开始时间在当前部分的结束时间之前 parts[j].sublst.append(parts[i]) parts[i].sublst.append(parts[j])
parts.sort(key=lambda x : len(x.sublst)) #按重叠数从小到大排列idx = 0while idx < len(parts)-1: #舍去重叠多的部门,推进直到倒数第二 if len(parts[idx].sublst) > 0 : #舍去重叠部门 for p in parts[idx].sublst: if p in parts: parts.remove(p) idx += 1print(len(parts))
解说:
策略是不冲突或少冲突的部门优先安排。为了实施这个策略,首先每个节点(部门)需要一个属性记录冲突的部门,然后按冲突部门数量排序,从小到大取值,同时舍去冲突部门,剩下的就是最多的部门。判定冲突,要先按开始时间排序,检查当前节点的后续节点的开始时间是否在当前节点的结束时间之前。
第四题编程实现:小贝要做一份黑暗料理,现有N(2≤N≤20)中不同的食材供她选择,食材编号从1到N。其中有些食材同时食用会产生副作用,所以产生副作用的食材只能选择其中一种食材或者都不选择。
已知同时食用会产生副作用的食材有M对(0≤M≤N*(N-1)/2),请计算出这份黑暗料理中最多能有多少种食材。
注意:会产生副作用的食材以两个编号表示,两个编号不等且编号小的在前,例如(1, 2)和(2, 3)。
例如:N= 5,M = 3时,5种食材编号为1到5,其中有3对食材会产生副作用:(1, 2)、(2, 3)、(4, 5)。
可选择1、3、4号食材或1、3、5号食材做黑暗料理,最多可以有3种食材。
输入描述:
第一行输入两个正整数N(2≤N≤20)和M(0≤M≤N*(N-1)/2),分别表示食材数量及会产生副作用的食材对数,两个正整数之间以一个空格隔开
接下来输入M行,每行两个正整数(1≤正整数≤N),表示会产生副作用的两种食材编号,两个正整数之间以一个空格隔开,两个编号不等且编号小的在前
输出描述:
输出一个整数,表示这份黑暗料理中最多能有多少种食材
样例输入:
5 3
1 2
2 3
4 5
样例输出:
3
代码:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
N, M = map(int, input().split()) # 输入N和Mclass Node(): #食材节点 def __init__(self): self.sublst=[] #冲突食材列表lst = [Node() for i in range(N)] #初始化食材,用一个列表记录冲突食材for i in range(M): x, y = map(lambda s : int(s)-1, input().split()) lst[x].sublst.append(lst[y]) #加入对象本身而不是下标 lst[y].sublst.append(lst[x])lst.sort(key=lambda x : len(x.sublst)) #按冲突从小到大排列idx = 0while idx < len(lst)-1: #推进直到倒数第二个,排除冲突食材的过程中保持排序 if len(lst[idx].sublst) > 0: #如果突出食材表非空 for i in lst[idx].sublst: if i in lst: lst.remove(i) #原食材表中排除该项 idx += 1print(len(lst))
解说:策略:副作用(冲突)没有或少的食材优先采用。为了实施这个策略,必然要先统计每个食材的冲突数。
第五题编程实现:小蓝从公司出发,要去拜访N(3≤N≤15)个客户,已知公司到每个客户的路程时间,及N个客户之间的路程时间。请计算出小蓝拜访完所有客户并返回到公司,最少需要多少时间。(道路双向通行,可重复走)例如:N = 3,有3个客户需要拜访,公司到1号、2号、3号客户的路程时间依次为9,7,5,客户1到客户2和客户3的路程时间依次是4,6,客户2到客户3的路程时间是3。 
从公司出发拜访完3名客户并返回公司最少需要的路程时间为21,行走路线为:公司 --> 3号 --> 2号 --> 1号--> 公司(21=5+3+4+9)。
输入描述:第一行输入一个正整数N(3≤N≤15),表示要拜访的客户数量第二行输入N个正整数(1≤正整数≤1000),依次表示公司到1号~N号客户的路程时间,正整数之间以一个空格隔开第三行输入N-1个正整数(1≤正整数≤1000),依次表示1号客户到2号~N号客户的路程时间,正整数之间以一个空格隔开第四行输入N-2个正整数(1≤正整数≤1000),依次表示2号客户到3号~N号客户的路程时间,正整数之间以一个空格隔开......第N+1行输入一个正整数(1≤正整数≤1000),表示N-1号客户到N号客户的路程时间输出描述:
输出一个整数,表示小蓝拜访完N名客户并返回公司最少需要的路程时间
样例输入:39 7 54 63样例输出:
21
代码:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
N = int(input()) # 客户数量dst = {} #距离字典,公司的编号0for i in range(N): #读取路程 ds = list(map(int, input().split())) for j in range(len(ds)): k = (i, i+1+j) #键,规定小的数在前,大的数在后的元组 dst[k] = ds[j]sumd = sum(dst.values()) #总路程def countd(sm, start, lst): #递归遍历全连通图 global sumd if len(lst) == 0: #走完所有客户,回公司 k = (0, start) sm += dst[k] if sm < sumd: sumd = sm return for i in range(len(lst)): end = lst[i] k = (start,end) if start < end else (end, start) sm += dst[k] countd(sm, end, lst[:i]+lst[i+1:]) #浅拷贝除了该元素的列表countd(0, 0, [i for i in range(1,N+1)])print(sumd)
解说:
这是一个全连通图遍历问题,只是在遍历过程中需要统计路程。为此引入一个词典,键是两个节点的元组(小的数在前),本处使用递归法遍历。
第六题编程实现:有一组正整数数据,现对这组数据按照如下操作:1)从这组数中找出两个相邻且相同的数,删掉其中一个数,剩下的一个数加1(例如:两个相邻的6,变成一个7);2)重复操作第1步,直到这组数据中没有相邻且相同的数时,操作结束。现给定N(1≤N≤2000)个正整数,表示这一组数,请问按照要求操作结束后,这组数据中最大的数是多少。注意:不同的操作方式得到的最后结果不同,要求最后的结果是所有操作方式中最大的。例如:当N=6,这组数为 1、2、2、2、3、4时,可获得最大结果的操作如下:第一次操作:将这组数据中后两个相邻的2,变成3,此时这组数变为1,2,3,3,4;第二次操作:将这组数据中两个相邻的3,变成4,此时这组数变为1,2,4,4;第三次操作:将这组数据中两个相邻的4,变成5,此时这组数变为1,2,5;此时这组数据中没有相邻且相同的数,操作结束,最大的数是5。非最大结果的操作如下:第一次操作:将这组数据中前两个相邻的2,变成3,此时这组数变为1,3,2,3,4;此时这组数据中没有相邻且相同的数,操作结束,最大的数是4。
所以按照要求操作结束后,这组数据中可获得的最大数是5。
输入描述:第一行输入一个正整数N(1≤N≤2000)第二行输入N个正整数(1≤正整数≤40),相邻两个数之间以一个空格隔开输出描述:
输出一个正整数,表示所有操作方式中最大的结果
样例输入:61 2 2 2 3 4样例输出:
5
代码:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
N = int(input()) #数字的个数lst = list(map(int, input().split())) #一组数maxNum = max(lst) #最大数def findRepeat(ls): #一次递归只操作一对重复元素 global maxNum rps = [] #重复位置 for i in range(1,len(ls)): if ls[i] == ls[i-1]: rps.append(i) if len(rps) == 0: #已经没有重复 maxNum = max(maxNum,max(ls)) return for i in rps: #浅拷贝除了两个重复元素的列表,重复位置用加1元素代替 findRepeat(ls[:i-1]+[ls[i]+1]+ls[i+1:])findRepeat(lst)print(maxNum)
解说:
由于从不同位置开始操作会产生不同的效果,因此每操作一对重复元素之后,生成的列表要作为一个新的问题处理。采用一次递归只操作一对重复元素,问题就迎刃而解。