第一题 背景知识
把二项式(a + b)^n展开式的的系数按(n = 0, 1, 2, 3, ……)逐行左右对称扩张排列,构成了一个等腰三角形。我们把这个三角形叫做杨辉三角形,因为杨辉发现了下面两个规律:
(1)首尾2数都是1,其它数是左上方和右上方的数之和;
(2)第N(N=n+1)行有N个数。

编程求解 从三角形的顶点出发到三角形的底,不同的累加和,及它的个数。如下图,1+1+2+3+6+10+20=43。

输入描述:
一个正整数N,表示杨辉三角形的层数。
输出描述:
从顶点出发不同路径的累加和的不重复值,就这些值的个数。
输入样例:
5
输出样例:5,8,10,11,12,13
6
代码(文本代码附录6):

解说:
本题所求是线路的累加和的集合,因此无需构造完整的杨辉三角形,在逐层推进时,统计线路的累加和就行。本处的节点采用系数值和累加集合的二元组,第一行是:[(1,set([1]))]。 推进下一行时,采用上一行分别首尾加一个0元素(系数值0,累加集合只有一个元素是该层)。
·
·
·
·
·
·
for i in range(1,N): L1 = [(0,set([i]))] + line L2 = line + [(0,set([i]))] line = [] #新的一行 for j in range(i+1): #新的一行 line.append(createItem(L1[j],L2[j]))
构建元素复杂了些,采用一个函数createItem完成。系数值是两个参数的系数和,累加集合是两个参数的累加结合的并集加该系数值。
·
·
·
·
·
·
·
def createItem(it1,it2): n = it1[0] + it2[0] s = it1[1] | it2[1] st = set() for i in s: st.add(i+n) return (n,st)
第二题
背景知识
x²+(p+q)x+pq型一元二次式因式分解法
我们发现
(x+p)(x+q)=x²+(p+q)x+pq
倒过来
x²+(p+q)x+pq=(x+p)(x+q)。
这个规律说明,只要把常数项分解为2个因数(注意正负号)的积,这两个因数的和等于一次项系数即可。
例如,分解因式
x²+3x+2,
2=1×2,1+2=3,
所以
x²+3x+2=(x+1)(x+2)。编程实现
编写一个实现x²+(p+q)x+pq型一元二次式因式分解的程序。
输入描述
两个非0整数,分别表示一次项系数(p+q)和常数项(pq),用因为逗号隔开。
输出描述
一条等式,左边是原整式,右边是整式分解;如果不可分解,打出整式后标注“不能分解因式!”。
样例输入1 3,2样例输出1
x²+3x+2=(x+1)(x+2)
样例输入2 3,3样例输出2
x²+3x+3不能分解因式!
代码(文本代码附录4):

解说: 用symbol记录常数项得符号后,对常数项进行因数分解。第一因数n从1开始往上增时,第二因数m从本值往下降,当待选的第一因数n超过第二因数m时,后面再也没有新的因数对,故分解过程结束。下面是标准的因数分解过程:
·
·
·
·
·
·
·
·
maxTestNum = p_multiply_q//2 #除了数的本身,最大可能因数 m = maxTestNum #第二个因数 #查找其它因数对 for n in range(2, maxTestNum+1): if n > m: #如果N已经超过上次的第二个因数,结束 break if p_multiply_q % n == 0: #找到一对因数 m = p_multiply_q // n #与n对应的第二因数
一次项和常数项得符号会影响判定规则和分解的结果表达形式,因此在checkAndPrint函数中分2×2=4中情况进行讨论:
·
·
·
·
·
·
·
·
·
·
if sym > 0: #常数项为正 if p_q > 0: #一次项为正值
else: #一次项为负值
else: #常数项为负 if p_q > 0: #一次项为正值
else: #一次项为负值
第三题
提示信息 有一个由多个小六边形组成的蜂巢图案,蜂巢外缘各边的小六边形数量一致,且左右对称。如下图:

以下为竖直对称线上小六边形个数为3、5、7的3个蜂巢图案。



编程实现 有一只蜗牛要从竖直对称线顶端的小正六边形移动到底端的小正六边形中,它每次只能向它所在位置的小正六边形的左下方、正下方、右下方相邻的小正六边形处移动。如下图所示:
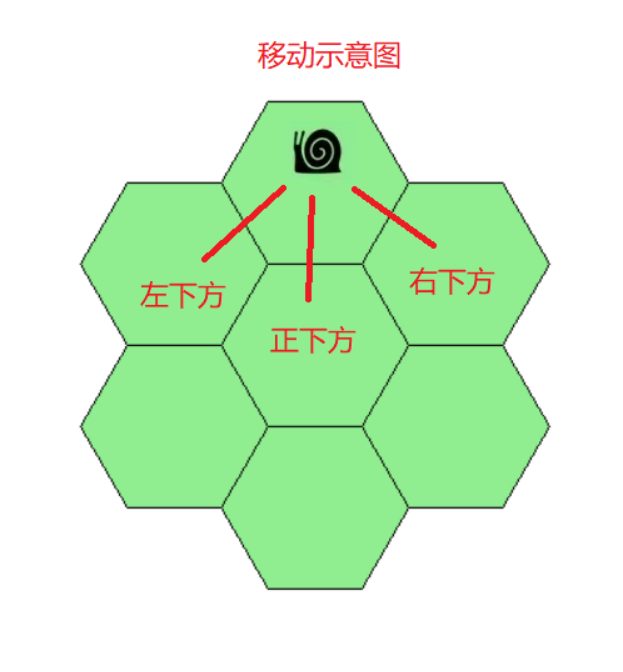
已知竖直对称线上有N个小正六边形,请计算出蜗牛从竖直对称顶端移动到底端共有多少条不同的移动路线。 例如:N=3,竖直对称线上有3个小正六边形,如下图:
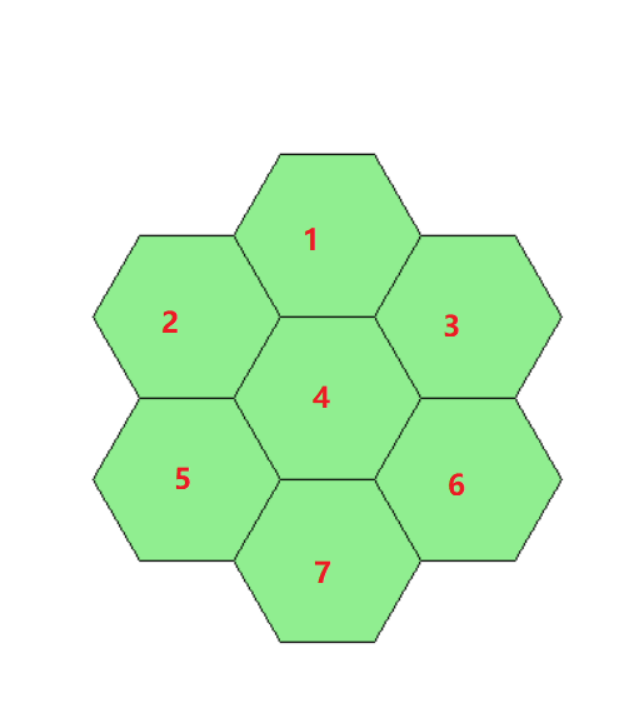
蜗牛从竖直对称线顶端的小正六边形中(1号处)移动到底端的小正六边形中(7号)共有11条不同的路线,分别为:
(1->2->5->7),(1->2->4->7),(1->2->4->5->7),(1->2->4->6->7),(1,4,5,7),(1->4->7),(1->4->6->7),(1->3->4->5->7),(1->3->4->7),(1->3->4>6>7),(1->3->6-7)。
输入描述
输入一个正奇数N(n<N<30),表示图案竖直对称线上小正六边形的个数。
输出描述
输出一个正整数,表示蜗牛从竖直对称线顶端移动到底端共有多少条不同的移动路线。
样例输入
3
样例输出
11
递归代码(文本代码附录1):

循环代码(文本代码附录2): 解说:
解说:

如上图,任一竖直的列把蜂巢分为左右两部分,每一行都是一条折线,折点是这条竖直的列,左点向下和向右都进入下一行,右点向下和向左也都进入下一行,竖直列上的一点只有向下才进入下一行。 从0开始向下进行行编号(0,1,2,...),左边的列为负,右边的列为正,这就是蜂巢平面的坐标系。很自然就得到移到的方法:
·
·
·
·
·
·
#左下移move(row + 1 if col > 0 else row, col - 1) #递归调用#正下移move(row + 1, col)#右下移move(row + 1 if col < 0 else row, col + 1)
加入到达终点的代码:
·
·
·
·
global count if row == N - 1 and col == 0: #到达终点 count += 1 return
左右越界容易得到,关键是左下和右下的越界。通过对坐标的观察容易得到,左下和右下的边界的行列坐标的绝对值之和是恒定的,从而得到越界代码:
·
·
·
if col < -(N-1)//2 or col > (N-1)//2 or abs(col)+row > N -1: #越界 return
第四题 在一面墙上,有n列边长为1的正方形瓷砖贴在上面(1≤n≤106),每列瓷砖的数量p(1≤p≤104,相邻列之间不留空隙)。现想在最大的矩形的瓷砖上画上壁画,小明目测一下很快就指出这个矩形,但别人不相信,请编程找出这个最大的矩形,证明小明的目测是否正确。
例如:n=6,即有6列瓷砖贴在墙上,每列瓷砖的数量依次为2,3,1,6,5,2,如下图:

图中矩形(阴影部分)面积最大,是10。
输入描述:
第一行输入瓷砖的列数n(正整数,1≤n≤106)
第二行输入n瓷砖的数量p(正整数,1≤p≤104,用空格隔开)
输出描述:
最大的矩形面积(正整数)
输入样例:
6
2 3 1 6 5 2
输出样例:
10
代码(文本代码附录5)

解说:
在一层中连续有瓷砖,那么它下面一定也是连续的瓷砖。这样把数据转化为只含0和1的二维列表(一列瓷砖是行,利于补全数据),按列进行统计。 找出最高的瓷砖柱,进行数据转换:
·
·
·
·
·
#构建01矩阵maxHeight = max(nums) #最高的柱mx = []for i in range(n): mx.append([1]*nums[i]+[0]*(maxHeight-nums[i]))
找出最低的瓷砖柱,计算开始面积:
·
·
·
minHeight = min(nums)#最大面积maxA = minHeight * n
从最低层的上一层开始统计,首先定位非0位置:
·
·
·
·
·
·
for i in range(minHeight,maxHeight): s = 0 j = 0 while j < n: while j < n and mx[j][i] == 0: #定位到非0 j += 1
然后,扫描连续的1的个数后计算该块矩形的面积:
·
·
·
·
·
·
·
·
while j < n and mx[j][i] > 0: #连续块 s += 1 j += 1 if s > 0: tmp = s * (i+1) #矩形面积 if tmp > maxA: maxA = tmp s = 0
第五题
提示信息: 有一个密室逃脱游戏,有100间密室连在一排。密室编号是从1开始连续排列一直排到第100间密室,如下图: 游戏规则: 1. 玩家初始位置在1号密室; 2. 每次玩家可以进入右边的一个密室,也可以跳过一个密室进入下个密室(如:当玩家当前在3号密室,他可以进入4号密室也可以进入5号密室),也可以跳过两个密室;
游戏规则: 1. 玩家初始位置在1号密室; 2. 每次玩家可以进入右边的一个密室,也可以跳过一个密室进入下个密室(如:当玩家当前在3号密室,他可以进入4号密室也可以进入5号密室),也可以跳过两个密室;
3. 有毒气的密室不能进入需要避开。
编程实现: 给定三个正整数X,Y,M(X<Y<M≤100),表示三个密室编号。X号密室和Y号密室有毒气泄漏,不能进入,玩家需要进入到M号密室。按照游戏规则进入M号密室有多少种路线方案。
例如:X=2,Y=4,M=7,进入M号密室有3种路线方案,分别是1->3->5->6->7路线、1->3->5->7路线和1->3->6->7路线。
输入描述:输入三个正整数X,Y,M(X<Y<M),X和Y表示有毒气密室编号,M表示需要进入的密室编号,且三个正整数之间以英文逗号隔开
输出描述:输出进入M号密室有多少种路线方案
样例输入:2,4,7
样例输出:3
代码(文本代码附录7):
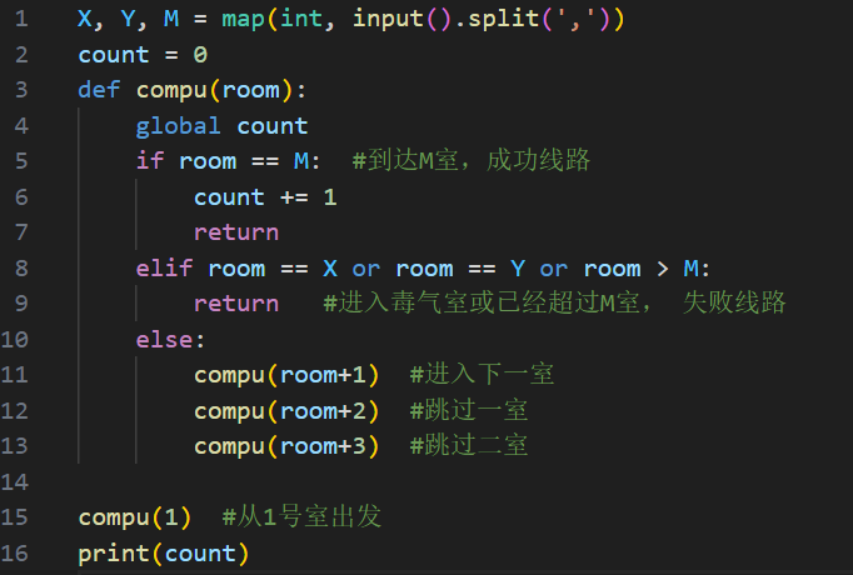
解说:
首先忽略限制条件(没有毒气泄漏),从1号室到M号室有多少种走法,假如M=7,线路绘图如下:

由图可见没有限制条件,从1号室到7号室有24种路径,下面采用递归法计算比较结果:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
M = 7count = 0def compu(room): global count if room == M: count += 1 return elif room > M: return else: compu(room+1) compu(room+2) compu(room+3)compu(1)print(count)
运行结果是24。现在加入不能经2,4号室,即把经过2,4号室的路径删除,如下图:

可见有3种方案。加入过滤条件,程序如下:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
X, Y, M = 2, 4, 7count = 0def compu(room): global count if room == M: count += 1 return elif room == X or room == Y or room > M: return else: compu(room+1) compu(room+2) compu(room+3) compu(1)print(count)
结果是3。
第六题 给出一排黑色带数字的小球(数字为0到9),和一排白色带数字的小球(数字为0到9),现从两排小球 中一共选取K个小球排成一排。 要求: 1)选出的黑色小球顺序要和原来顺序一致; 2)选出的白色小球顺序要和原来顺序一致; 在满足以上要求的情况下,使得K个小球排成新的一排组成的数字最大 例如:黑色小球的原顺序为:Ž 白色小球的原顺序为: †‚„ K为3; 从两排小球中共选取3个小球,排成†„。可以组成的最大数字为654。 输入描述: 第一行输入一组正整数,代表黑色小球,每个正整数范围为0到9,正整数之间以一个英文逗号隔开 第二行输入一组正整数,代表白色小球,每个正整数范围为0到9,正整数之间以一个英文逗号隔开 第三行输入一个正整数K(K小于等于所有小球的总数),表示从所有小球中共选取K个小球 输出描述: 输出一个整数,表示按照要求选取K个小球后,组成的最大数字 样例输入: 2,5,3 6,2,4,1 3 样例输出: 654代码(文本代码附录8):

解说: 如果每一次都是取两个列表混在一起的最大值,那么这个数就是最大的数(减少限制条件是获得解题思路的重要方法!)。但是由于要保持顺序,取最大的值可能造成后续的元素不够,这样就不得不舍而求次,直到后续有足够元素为止。 每一个数除了值的大小外,还有处于哪个列表和在列表中的位置,因此我们不能把它作为一个数来考虑,而应该作为数据结构的元素——节点。对象化编程思想往往能够把复杂的问题简单化,因为对象可以保持状态属性。
每一个节点需要保留三个值——列表号、数值和位置。本文为了照顾没有掌握使用类的学生,使用一个三元素列表作为节点,依次为源列表号、数值和下标。合并两个列表的节点为一个节点,然后根据节点的值倒叙排序。
·
·
lst= [[1,int(iptlsb[i]),i] for i in range(len(iptlsb))] + [[2,int(iptlsw[i]),i] for i in range(len(iptlsw))]lst.sort(key=lambda x:x[1], reverse=True)
从排好序的混合列表中按顺序取出一个节点放入结果列表中,剩下的混合列表递归获取最大的K-1位数——作为一个方案。如果由于条件限制无法完成,方案返回False,清理结果列表进入下一个方案的检查,最后必然有一个方案返回True。
·
·
·
·
·
·
·
for i in range(len(lst)):rst.append(lst[i])if find(0, lst[:i]+lst[i+1:]):print(''.join(map(str,[i[1] for i in rst])))breakelse:rst.clear()
递归函数find(开始下标,取出了方案节点的混合列表)需要完成下面的任务:首先判定结果是否已经达到K个,如果是就返回True;然后检查下标是否越界,如果是就返回False;第三检查当前下标的节点是否在结果集的前面,如果是就下推一个下标,递归调用;最后把该下标的节点加入结果列表,同样下推一个下标,递归调用。
·
·
·
·
·
·
·
·
·
def find(index, ls):if len(rst)==K:return Trueif index==len(ls):return Falseif checkBeforeResult(index, ls):return find(index+1, ls)rst.append(ls[index])return find(index+1, ls)
函数checkBeforeResult(当前下标,取出了方案节点的混合列表)检查当前节点是否在结果列表中任一个节点的前面。
·
·
·
·
·
·
·
·
def checkBeforeResult(index, ls):if len(rst)==0:return Falsea=ls[index]for t in rst:if t[0]==a[0] and t[2]>a[2]:return Truereturn False
后语:
由于时间比较仓促,难免有错漏,请指正;另外,如果无法看懂代码,请留言或加微信www_5xstar_com/13729135043。
已发蓝桥杯真题解(可作为STEMA测评参考):
第十四届蓝桥杯青少组Python国赛真题解(全卷2023-8-2)(可作为STEMA测评参考)
第十四届蓝桥杯青少组Python省赛真题解(可作为STEMA测评参考)
第十三届蓝桥杯青少组Python国赛真题解(可作为STEMA测评参考)
第十三届蓝桥杯青少组Python省赛真题解(可作为STEMA测评参考)
第十二届蓝桥杯青少组Python国赛真题解(可作为STEMA测评参考)
第十二届蓝桥杯青少组Python省赛真题解(可作为STEMA测评参考)
第十一届蓝桥杯青少组Python国赛真题解(可作为STEMA测评参考)
第十一届蓝桥杯青少组Python省赛真题解(可作为STEMA测评参考)
第十届蓝桥杯青少组Python省赛真题解(可作为STEMA测评参考)
蓝桥杯青少组Python编程练习题解 第一集(可作为STEMA测评参考)
更多资料请点开:
附录1:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
N = int(input())count = 0 #方案数 #递归移动def move(row,col): global count if row == N - 1 and col == 0: #到达终点 count += 1 return if col < -(N-1)//2 or col > (N-1)//2 or abs(col)+row > N -1: #越界 return #左下移 move(row + 1 if col > 0 else row, col - 1) #递归调用 #正下移 move(row + 1, col) #右下移 move(row + 1 if col < 0 else row, col + 1)
move(0,0)print(count)
附录2:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
N = int(input())count = 0 #方案数 #循环移动lst1 = [(0,0)]lst2 = []while len(lst1) > 0:for row, col in lst1:if row == N - 1 and col == 0: #到达终点count += 1continueif col < -(N-1)//2 or col > (N-1)//2 or abs(col)+row > N -1: #越界continue#左下移lst2.append((row + 1 if col > 0 else row, col - 1)) #正下移lst2.append((row + 1, col))#右下移lst2.append((row + 1 if col < 0 else row, col + 1))
lst1 = lst2lst2 = []
print(count)
附录3:组合正六边形海龟画图
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
import turtle as tt.speed(0)#t.tracer(False)t.ht()n=3m=(n+1)//2a=60startY = 200 #绘图y参考线t.fillcolor(<span data-raw-text="" "="" data-textnode-index-1685687091320="262" data-index-1685687091320="1594" data-textnode-notemoji-index-1685687091320="1594" class="character">"lightgreen<span data-raw-text="" "="" data-textnode-index-1685687091320="262" data-index-1685687091320="1605" data-textnode-notemoji-index-1685687091320="1605" class="character">")
def draw_six(): #绘制一个小正六边形t.begin_fill()for i in range(6):t.fd(a)t.lt(60)t.end_fill()
def draw_col(y0,cn):'''@y0 该列开始绘制位置@cn 该列的小六边形个数'''for j in range(cn):t.pu()t.sety(y0-3**0.5*a*j)t.pd()draw_six()
def draw_row(sn):'''@sn -1绘制左边,1绘制右边'''for k in range(1,m):t.pu()y0 = startY-3**0.5*a/2*kt.goto(sn*3*a/2*k, y0) t.pd()draw_col(y0,n-k)
draw_col(startY,n)draw_row(-1)draw_row(1)
t.mainloop()
附录4:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
#x²+(p+q)x+pq型一元二次式因式分解#p+q=一次项系数检查,如果通过就打印,返回Truedef checkAndPrint(p_q, pq, sym, p, q): '''@p_q一次项系数,原值 @pq常数项绝对值 @sym常数项符号±1 @p和q待检查的常数项因数 正整数''' if sym > 0: #常数项为正 if p_q > 0: #一次项为正值 if p_q == p + q: #两因数和等于一次项系数,,两因数同为正值 print("x²+%dx+%d=(x+%d)(x+%d)" %(p_q, pq, p, q)) return True else: #一次项为负值 if -p_q == p + q: #两因数和等于一次项系数的相反数,两因数同为负值 print("x²-%dx+%d=(x-%d)(x-%d)" %(-p_q, pq, p, q)) return True else: #常数项为负 if p_q > 0: #一次项为正值 if p_q == abs(p - q): #两因数的差的绝对值等于一次项系数,大的因数为正 if p > q: print("x²+%dx-%d=(x+%d)(x-%d)" %(p_q, pq, p, q)) else: print("x²+%dx-%d=(x-%d)(x+%d)" %(p_q, pq, p, q)) return True else: #一次项为负值 if -p_q == abs(p - q): #两因数的差的绝对值等于一次项系数的相反数,大的因数为负 if p > q: print("x²-%dx-%d=(x-%d)(x+%d)" %(-p_q, pq, p, q)) else: print("x²-%dx-%d=(x+%d)(x-%d)" %(-p_q, pq, p, q)) return True return False
#主函数def main(): #一次系数,常数项 p_plus_q, p_multiply_q = map(int, input().split(',')) #常数项符号,-1表示常数项为负,则因数符号不同;1表示数项为正,则因数符号相同 if p_multiply_q < 0: symbol = -1 p_multiply_q = -p_multiply_q #相反数,为正数 else: symbol = 1 #检查首对因数:1和本身 if checkAndPrint(p_plus_q, p_multiply_q, symbol, 1, p_multiply_q): return
maxTestNum = p_multiply_q//2 #除了数的本身,最大可能因数 m = maxTestNum #第二个因数 #查找其它因数对 hasFinded = False #是否发现 for n in range(2, maxTestNum+1): if n > m: #如果N已经超过上次的第二个因数,结束 break if p_multiply_q % n == 0: #找到一对因数 m = p_multiply_q // n #与n对应的第二因数 if checkAndPrint(p_plus_q, p_multiply_q, symbol, n, m): #检查 hasFinded = True #设置成功变量 break #退出循环
#打印不可分解 if not hasFinded: if symbol > 0: if p_plus_q > 0: print("x²+%dx+%d不能分解因式!" %(p_plus_q, p_multiply_q)) else: print("x²-%dx+%d不能分解因式!" %(-p_plus_q, p_multiply_q)) else: if p_plus_q > 0: print("x²+%dx-%d不能分解因式!" %(p_plus_q, p_multiply_q)) else: print("x²-%dx-%d不能分解因式!" %(-p_plus_q, p_multiply_q))
if __name__ == "__main__": main()
附录5:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
n = int(input())nums = list(map(int,input().split()))#构建01矩阵maxHeight = max(nums) #最高的柱mx = []for i in range(n): mx.append([1]*nums[i]+[0]*(maxHeight-nums[i]))minHeight = min(nums)#最大面积maxA = minHeight * n#分层统计for i in range(minHeight,maxHeight): s = 0 j = 0 while j < n: while j < n and mx[j][i] == 0: #定位到非0 j += 1 while j < n and mx[j][i] > 0: #连续块 s += 1 j += 1 if s > 0: tmp = s * (i+1) #矩形面积 if tmp > maxA: maxA = tmp s = 0
print(maxA)
附录6:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
N = int(input())#创建一个元素def createItem(it1,it2): n = it1[0] + it2[0] s = it1[1] | it2[1] st = set() for i in s: st.add(i+n) return (n,st)
line = [(1,set([1]))] #杨辉三角形的一行for i in range(1,N): L1 = [(0,set([i]))] + line L2 = line + [(0,set([i]))] line = [] #新的一行 for j in range(i+1): #新的一行 line.append(createItem(L1[j],L2[j]))
rst = set() #合并集合for it in line: rst |= it[1]
print(",".join(map(str,rst)))print(len(rst))
附录7:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
X, Y, M = map(int, input().split(','))count = 0def compu(room): global count if room == M: #到达M室,成功线路 count += 1 return elif room == X or room == Y or room > M: return #进入毒气室或已经超过M室, 失败线路 else: compu(room+1) #进入下一室 compu(room+2) #跳过一室 compu(room+3) #跳过二室
compu(1) #从1号室出发print(count)
附录8:
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
iptlsb= input().split(',')iptlsw= input().split(',')K=int(input())#合并两组数,标识组号和位置lst= [[1,int(iptlsb[i]),i] for i in range(len(iptlsb))] \ + [[2,int(iptlsw[i]),i] for i in range(len(iptlsw))]#按数值从大到小排列lst.sort(key=lambda x:x[1], reverse=True)#结果列表rst=[]def find(index, ls): if len(rst)==K: return True if index==len(ls): return False if checkBeforeResult(index, ls): return find(index+1, ls) rst.append(ls[index]) return find(index+1, ls)def checkBeforeResult(index, ls): if len(rst)==0: return False a=ls[index] for t in rst: if t[0]==a[0] and t[2]>a[2]: return True return Falsefor i in range(len(lst)): rst.append(lst[i]) if find(0, lst[:i]+lst[i+1:]): print(''.join(map(str,[i[1] for i in rst]))) break else: rst.clear()