汉诺塔(又称河内塔)问题是源于印度的一个古老传说。大梵天创造世界时做了三根金刚石柱子,在一根柱子上从上往下按照由小到大的顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘重新摆放在另一根柱子上,顺序同样是从上往下由小到大摞列。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。下面是7层汉诺塔视频。
把要求简述如下:a、b、c三根柱子,a上有从上到下按从小到大顺序摞着一列圆盘,现要求把a柱子上所有的圆盘移动到c柱子上。移动规则如下:
(1)三根柱子之间一次只能移动一个圆盘。
(2)任何情况下,大圆盘不能放在小圆盘上面。
解题思路:三个用途在三根柱子中是来回切换的。情况比较复杂,优先考虑用递归算法。根据递归算法的要求,首先看看碟子数量较少的情况能否解决。
(1)当a柱上只有一个盘子时,直接将盘子移动到c柱上,如下图所示。
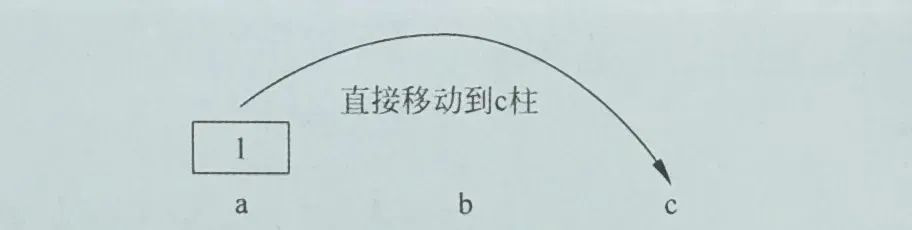
(2)当a柱上有2个盘子时,操作步骤如图下图所示。

(3)当a柱上有3个盘子时,操作步骤如图下图所示。
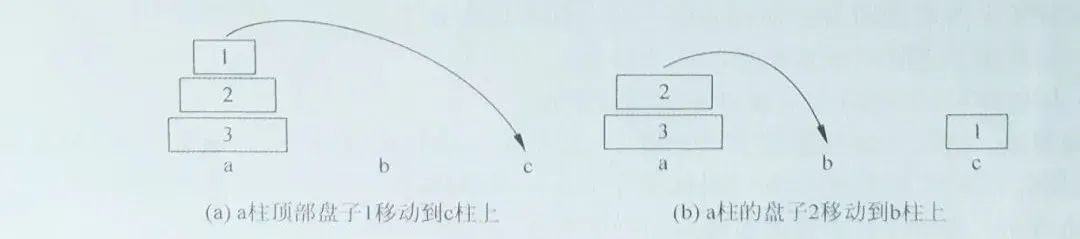

显然,一到三个盘子的情况都是可以解决的。然后考虑n个盘子的情况,假设能把n-1个盘子移动到b柱上,把最大的盘子移到c柱上。这样又可以视作一个移动n-1个碟子的汉诺塔游戏,所以问题必然是可以用递归方法解决。
算法分析:各个柱子在这过程中作用是变化的,为了操作的统一性,定义三个角色:源柱子、中间柱子和目标柱子。递归过程就是把步骤分解成下面的三个子步骤。
(1)设源柱子上落有n个盘子,将前n一1个盘子从源柱子移动到中间柱子上。
(2)将最底下的最后一个盘子从源柱子移动到目标柱子上。
(3)将中间柱子上的n一1个盘子移动到目标柱子上。
把(1)和(3)看做一次独立的n-1汉诺塔游戏,也就可以继续分解直到要移动1个盘子。
柱子每次只能操作最上面的盘子,所以是栈,用栈来表示柱子。为了方便区分柱子,在Stack类中加入name属性。

测试程序:


打印结果:

例题1:盘子是越多,搬动次数越多,那么64个盘子一共要搬动多少次呢?,,
分析:因为要搬动底盘子,需要把它上的盘子全搬到中间柱子,然后把底盘子搬到目标柱子,然后把中间柱子的盘子全搬到目标柱子,所以,假如n个盘子的搬动次数是M次,那么n+1个盘子是2M+1次。那么4个盘子是:
((1*2+1)×2+1)×2+1=15次。
上面的程序正是搬动15次。
程序代码:

运行结果:

练习题:本文开头的视频是Python海龟画图制作的,代码附录中,请把代码抄到Python文件后运行。
学思营编程课堂基于蓝桥STEM86平台https://www.stem86.com,开展学编程三部曲:Scratch(三年级以前)>>>Python(四年级以后)>>>C++(七年级以后)教育实验活动,任何人可以免费参加,打开https://xuesiying.stem86.com网页注册进入课堂,也可关注本公众号留言。更多课程请打开“学思营”同步网站:http://www.5xstar.com/doc.html
参考资料:
1、《Python算法图解》何韬编著 清华大学出版社
附录:
import turtle as t #导入海龟画图并把它重命名为t
import time #导入时间模块
#初始化海龟
t.title("递归汉诺塔——学思营https://xuesiying.stem86.com") #设置标题
t.setup(500, 500) #把窗口初始化
t.screensize(400, 400) #画布大小
#数据节点
class Node:
def __init__(self, value): #节点初始化
self.value = value #节点的值
self.pre = None #指向前一个节点的指针
#栈
class Stack:
def __init__(self, name=None, location=None): #栈初始化
'''
@name为栈名
@location为初始位置
'''
self.point = None #定义栈顶指针
self.length = 0 #栈中节点总数
self.name = name
self.location =location
def push(self, value): #向栈中压入数据方法
node= Node( value) #把压入栈中的数据包装成栈节点
if self.point != None: #假如栈顶指针不为空
node.pre = self.point #后压入栈的节点指向前一个节点
self.point = node #栈顶指针指向新压入栈的新节点
else: #假如栈顶指针为空
self.point = node #栈顶指针指向栈中唯一的节点
self.length += 1 #栈中总数加1
add(self, node) #加入海龟
def pop(self): #从栈中弹出数据方法
if self.point != None: #假如栈顶指针不为空
node = self.point #获得栈顶指针指向的节点
self.point = node.pre #栈顶指针向前一个节点移动
node.pre = None #把栈顶节点的向前指针置为空
self.length -= 1 #栈中节点总数减1
div(self, node) #减一节点
return node.value #返回弹出节点的值
else: #如果栈内没有节点
return None #返回空
def isNone(self): #栈的判空方法
if self.length>0: #假如栈内节点总数大于0
return False #返回False
else: #假如栈内节点总数等于0
return True #返回True
#加入海龟
def add(stack, node):
stack.location = stack.location[0], stack.location[1]+25 #y坐标上一台阶
node.value.st()
node.value.setpos(stack.location) #移动海龟
#减1海龟
def div(stack, node):
stack.location = stack.location[0], stack.location[1]-25 #y坐标下一台阶
node.value.ht()
#递归,层层分解
def move(n, s1, s2, s3):
'''
@n 塔的层数
@s1 原塔
@s2 中间塔
@s3 目的塔
'''
if n != 1:
move(n-1, s1, s3, s2) #把底座上面所有盘子移动到中间柱子上
move(1, s1, s2, s3) #移动底座盘子到目标柱上
move(n-1,s2, s1, s3) #把中间柱子上的盘子移动到目标柱子上
else: #当只剩一个盘子时
#s1 -> s3
s3.push(s1.pop()) #把盘子移动到目标柱子上
print(s1.name, '=>', s3.name) #打印移动盘
t.up() #提笔
posA=(-100, -100) #A塔位置
t.setpos(posA[0],posA[1]) #A塔写上标签A
t.write("A", align="center", font=("黑体", 14, "normal")) #居中14号
a = Stack('A', posA) #声明1个栈——第1根柱子起名叫A
posB=(0, -100)
t.setpos(posB[0],posB[1])
t.write("B", align="center", font=("黑体", 14, "normal"))
b = Stack('B', posB) #声明b柱子
posC=(100, -100)
t.setpos(posC[0],posC[1])
t.write("C", align="center", font=("黑体", 14, "normal"))
c = Stack('C', posC) #声明c柱子
t.shape("square") #采用正方形海龟
t.seth(90) #海龟朝上
t.speed(3) #海龟慢速移动
print("海龟画图初始化完成,3秒后构建7层汉诺塔。")
time.sleep(3) #暂停3秒
temp = t.clone() #克隆海龟 最大的碟子,黑色
temp.shapesize(5, 0.5, 1) #横向5倍,同向0.5, 边框1
a.push(temp) #加入A栈
temp = t.clone()
temp.shapesize(4.5, 0.5, 1)
temp.fillcolor("#FF0000") #填充颜色
temp.pencolor("#FF0000") #画笔颜色
a.push(temp)
temp = t.clone()
temp.shapesize(4, 0.5, 1)
temp.fillcolor("#FFFF00")
temp.pencolor("#FFFF00")
a.push(temp)
temp = t.clone()
temp.shapesize(3.5, 0.5, 1)
temp.fillcolor("#00FF00")
temp.pencolor("#00FF00")
a.push(temp)
temp = t.clone()
temp.shapesize(3, 0.5, 1)
temp.fillcolor("#00FFFF")
temp.pencolor("#00FFFF")
a.push(temp)
temp = t.clone()
temp.shapesize(2.5, 0.5, 1)
temp.fillcolor("#0000FF")
temp.pencolor("#0000FF")
a.push(temp)
temp = t.clone()
temp.shapesize(2, 0.5, 1)
temp.fillcolor("#FF00FF")
temp.pencolor("#FF00FF")
a.push(temp)
t.ht() #隐藏海龟
print("7层汉诺塔初始化完成,3秒后移动。")
time.sleep(3)
n = a.length
move(n, a, b, c)