例题12：构造带环的单向链表。

　　单向链表的尾节点的next指针指向自身的某个节点，会在自身链表上形成一个环，如下拓扑图所示。

　　尾节点这种带环的单向链表会在遍历时形成死闭合节点环，无穷尽地转图遍历。先看这种链表是如何构成的，下面先写程序把单向链表改造成一个带环的链表，程序实现步骤如下：

　　(1)找到构成闭环的闭合节点。

　　(2)找到尾节点。

　　(3)尾节点的next指针指向闭合节点。

　　程序代码：

　　运行结果：

　　练习题１：如果上例的linkList.setCircle(3)改为linkList.setCircle(-1)、linkList.setCircle(0)、linkList.setCircle(5)、linkList.setCircle(7)、linkList.setCircle(8)、linkList.setCircle(9)、linkList.setCircle(10)和linkList.setCircle(11)，运行结果分别是什么？

　　例题13：假如链表长度不知，判断链表是否有环并找出环的闭合点。

　　数学分析：在环中运动的物体，速度快的最终会绕一圈追上慢的，这个原理同样适合判定链表是否有环。如下图：

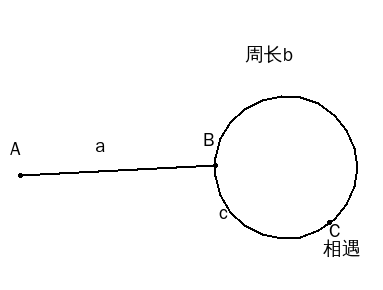
AB距离是a，圆的周长是b，甲乙同时从A出发，乙的速度是甲的2倍，进入圆环后都是逆时针运动，在距离B点的逆时针距离c的点C处相遇。证明如果甲在A点，乙减速与甲相同在C点同时出发，他们会在B点相遇。

　　证明：

当他们在C点相遇时，乙走的距离是甲走的距离的2倍，设甲绕了m圈，乙绕了n圈，即

2(a+mb+c)=a+nb+c。

移项，得

a+2mb = nb - c。

　　如果他们速度相同，等式左边说明甲走a+2mb距离时在Ｂ点；等式右边说明乙走了n圈少c，也是B点，所以他们在B点相遇。

　　数学证明虽然严谨，但不好理解。可以这样理解：由于他们相遇于环里，后来他们以相同速度走，由于同样的时间他们走的距离一样，因此他们必然会在C点又相遇，由于速度相同，那么在B到C都是在一起的，所以必然相遇于B点。

　　算法分析：

　　(1)判断是否有环：声明快慢两个指针，快指针一次向后移动两步，慢指针一次向后移动一步。如果有环，快指针就能追上慢指针（如果没有环，快指针不可能绕到慢指针后再追上慢指针）。快慢指针如果在某个时刻相会，则链表有环：如果快指针走到最后一个节点发现后续为空，则链表无环。

　　(2)找出环的闭合点：留快指针在相遇点，慢指针重置到链表头节点。然后同时同步顺着链表移动，快指针会在环中转圈，而慢指针会与快指针相遇于在闭合点。

　　程序代码：

　　运行结果：

　　练习题２：如果上例的linkList.setCircle(3)改为linkList.setCircle(0)、linkList.setCircle(1)、linkList.setCircle(2)、linkList.setCircle(4)、linkList.setCircle(5)、linkList.setCircle(6)和linkList.setCircle(7)，看看判定是否正确？

　　练习题３：其实链表是有长度，链表的length-1个节点就是尾点，如果尾点的后续指针为空，那就无环，否则有环，尾指针所指向的节点就是闭合点。用这种方法编写一个程序，判定单向链表是否有环并查出闭合点。

　　学思营编程课堂基于蓝桥STEM86平台https://www.stem86.com，开展学编程三部曲：Scratch（三年级以前）>>>Python（四年级以后）>>>C++（七年级以后）教育实验活动，任何人可以免费参加，打开https://xuesiying.stem86.com网页注册进入课堂，也可关注本公众号留言。更多课程请打开“学思营”同步网站：http://www.5xstar.com/doc.html

参考资料：

１、《Python算法图解》何韬编著　清华大学出版社