对于一般的二叉搜索树，从效率上看期望它的节点是尽可能左右平衡、排布均匀的。一棵左右节点比较均衡的二叉树，对它操作的时间复杂度是最低的。但是，在某些极端的情况下（如插入的序列是有序的），二叉搜索树将退化成近似链表，此时其操作的时间复杂度将退化成线性的，如同链表。这就大大降低了树的搜索效率，如下图所示。

　　如何提高二叉树的查找效率呢，平衡二叉树是一个解决方案。如果二叉树中每个节点的左子树和右子树的深度相差不超过1，称作平衡二叉树。也就是说，要么它是一棵空树，要么它的主树和所有子树的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。

　　我们把节点的左子树深度减右子树深度之差称作平衡因子。它作为判断一棵二叉树是不是一棵平衡二叉树的标准。为了便于运算，在平衡二叉树节点的数据结构体增加一个整型属性，用来记录该节点的平衡因子。平衡二叉树的平衡因子只能取（-1,0,1），否则就不是平衡二叉树，如下图所示。

　　平衡二叉树的节点插入

　　根据平衡二叉树的概念，当一棵二叉树的节点超过2时，就可能失去平衡，如何向一棵树（至少有2个节点）中插入一个新节点后还保持平衡状态呢？也就是说，插入节点时，每个节点的平衡因子绝对值不超过1。解铃还须系铃人，产生不平衡的原因是什么呢？

　　我们知道二叉树左树小，右树大；对于任一节点，左树右树节点数差别大是产生不平衡的根本原因。因此，使所有节点的左右树节点数量均衡就能到达平衡的目的。

　　节点数平衡法：树中每个节点的左右总数差值最多相差一个，如果超过立刻纠正。原来的平衡因子已不适合使用，改为：节点数平衡因子=左子节点数－右子节点数。这个方法的依据：左右树的深度差不超过节点数差。节点数平衡法是平衡二叉树的充分条件，生成的平衡二叉树是平衡二叉树的子集。也就是说，某些平衡二叉树是不能用节点数平衡法生成的。举例说明，一个由五个节点[1,2,3,4,5]构成的所有平衡二叉树如下图：

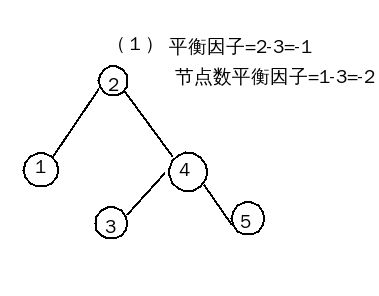
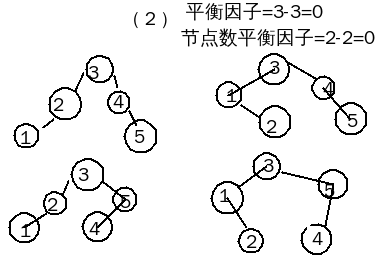
由图可见，按节点数平衡因子算，只有（２）才是平衡二叉树，但实际上它们都是平衡二叉树。由于节点数平衡法相对比较简单，这里采用它进行计算。

　　算法逻辑：

　　(1)根节点的节点数平衡因子在插入前是1，当插入小于根节点数值的节点时就一定变成2了，于是需要调整。调整的方法自然是把左子树一个节点调到右子树；但节点的左子树的所有节点值都小于该节点值；右子树的所有节点值都大于该节点值，因此实际的流动方法：

左子树最大值（删除）=>>根节点值（替换）=>>右子树（添加）。

　　(2)根节点的节点数平衡因子在插入前是-1，当插入大于根节点数值的节点时就一定变成-2了，于是需要调整。调整的方法自然是把右子树一个节点调用左子树，实际的流动方法：

右子树最小值（删除）=>>根节点值（替换）=>>左子树（添加）。

　　(3)左子树最大值（删除）方法：把左子树作为根节点，向右子树查找最大值，沿途记录最大值节点的祖先，并把所有祖先的节点数平衡因子加1（因为要删除右子树的节点）；删除最大值节点后，如果记录中有祖先，从第一个祖先开始检查平衡性，如果发现不平衡，用(1)或(2)方法调整；返回左子树最大值。

　　(4)右子树最小值（删除）方法：把右子树作为根节点，向左子树查找最小值，沿途记录最小值节点的祖先，并把所有祖先的节点数平衡因子减1（因为要删除左子树的节点）；删除最小值节点后，如果记录中有祖先，从第一个祖先开始检查平衡性，如果发现不平衡，用(1)或(2)方法调整；返回右子树最小值。

　　(5)节点值（替换）方法：用临时变量缓存节点值后，节点赋予新值。

　　(6)子树（添加）方法：把子树第一个节点当作根节点递归调用添加方法。

　　平衡二叉树分层遍历

　　为了更好地观察平衡二叉树的“平衡”性，采用满二叉树的分层遍历方法，即把平衡二叉树对应的满二叉树分层打印出来。

　　程序代码：

　　运行结果：

　　思考题１：请看下面的代码和运行结果，与上例比较，你能得出什么结论？

　　二叉树的降维：当一个系列是按二叉树的从上到下，从左到右的顺序排列时，顺次插入二叉树会恢复二叉树原来的结构。

　　不失一般性，用整数列表表示这个系列，然后把一个整数的平衡二叉树降维，就可以得到一个整数列表；反过来，如果能通过某种方法，把一个整数列表转变成符合平衡二叉树的顺序，升维后就可以得到平衡二叉树——暂时把这种方法叫做降维法。

　　在节点数平衡法中，树的根节点：当节点总数是奇数时，它是这些数的中值；当节点总数是偶数时，它是这些数的2个中值中的一个。同理，左子节点是小于中值的数中的中值；右子节点是大于中值的数中的中值......如此类推。因此，要用降维法构造平衡二叉树，首先要把数列按顺序排列，然后用中值取数构成新的列表，用新列表构造二叉树就是平衡二叉树。排序以后会学到，这里只讨论从已经排序的列表构造平衡二叉树的方法。

　　降维法在构造时并没有使用节点数平衡因子，但在查看时需要打出节点数平衡因子，因此还需要计算节点数平衡因子的算法：设计一个递归方法，分别算出左子树和右子树的节点数，然后用它们的差作为节点数平衡因子，返回它们的和加1（节点本身计数）。

　　程序代码：

　　运行结果：

　　练习１：用节点数平衡法把数据[2,1,4,3,5,6]构建平衡二叉树。

　　练习２：如果在上例的降维法构建平衡二叉树，输入的列表是倒序的[11,10,9,7,6,5,4,3,2,1,0,-1,-3]，还能构建成平衡二叉树吗？编程验证你的判断。

　　练习３：编写一个程序，可以用降维法初始化平衡二叉树，然后用节点数平衡法插入节点。初始化数据：[1,2,3,4,5,6,7,9,10,11]；插入数据：[0,-3,-1]。

　　学思营编程课堂基于蓝桥STEM86平台https://www.stem86.com，开展学编程三部曲：

Scratch（三年级以前）>>>Python（四年级以后）>>>C++（七年级以后）教育实验活动，任何人可以免费参加，打开https://xuesiying.stem86.com网页注册进入课堂，也可关注本公众号留言。

更多课程请打开“学思营”同步网站：

http://www.5xstar.com/doc.html

参考资料：

１、《Python算法图解》何韬编著　清华大学出版社