克鲁斯卡尔(Kruskal)算法查找最小生成树的方法是:将连通图中所有的边按照权值大小做升序排序,从权值最小的边开始选择,只要此边不和已选择的边一起构成环路,就可以选择它组成最小生成树。对于 N 个顶点的连通网,挑选出 N-1 条符合条件的边,这些边组成的生成树就是最小生成树。
图解下面的连通图的最小生成树。

克鲁斯卡尔(Kruskal)算法查找上图对应的最小生成树,需要经历以下几个步骤:
(1) 将连通网中的所有边按照权值大小做升序排序:

(2) 从 B-D 边开始挑选,由于尚未选择任何边组成最小生成树,且 B-D 自身不会构成环路,所以 B-D 边可以组成最小生成树。

(3) D-T 边不会和已选 B-D 边构成环路,可以组成最小生成树:

(4) A-C 边不会和已选 B-D、D-T 边构成环路,可以组成最小生成树:

(5) C-D 边不会和已选 A-C、B-D、D-T 边构成环路,可以组成最小生成树:
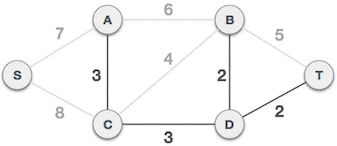
(6) C-B 边会和已选 C-D、B-D 边构成环路,因此不能组成最小生成树:

(7) B-T与B-D-T、A-B与A-C-D-B构成环路,都不能组成最小生成树。而 S-A 不会和已选边构成环路,可以组成最小生成树。

(8) 如上图所示,对于一个包含 6 个顶点的连通网,我们已经选择了 5 条边,这些边组成的生成树就是最小生成树。
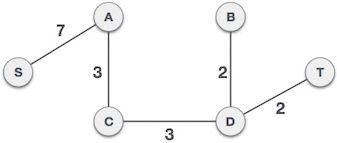
上面的过程中,我们运用了形象的判断环方法,但程序是很难实现的,因此需要做一些改动。对于树,都有一个基本特性:树在生长过程中,除了第一条边,其他边必然开始于已触达顶点,结束于未触达顶点。那么符合下面的条件就可以保证环不出现:
(1)只有1棵树在生长;
(2)除了首边,开始顶点已触达,结束顶点未触达。
算法逻辑:
(1)把第0边的开始顶点加入父顶点集,2个顶点都放到已触达顶点集中,第1边后放到当前扫描边集,声明一个空集作为下次扫描的边收集器。
(2)扫描当前边集:
(A)如果边的结束顶点已在已触达顶点集中,抛弃。然后,
(B)如果开始顶点在已触达顶点集中,把这边加到树中:结束顶点加入已触达顶点集,开始顶点加入父顶点集。然后,
(B1)如果已触达顶点达到总顶点数,完成,返回;
(B2)否则把未扫描的边放入下次扫描的边收集器中,终止当次循环。
(C)如果2点都不在已触达顶点集中,该边加入下次扫描的边收集器,继续当次循环。
邻接矩阵程序代码(文本代码附录1,基础类在上一课):






运行结果:

邻接表程序代码(文本代码附录2):






运行结果:

结果正是下面的树:
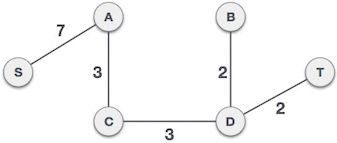
练习题1: 分别用邻接矩阵Kruskal和邻接表Kruskal算法计算下面图的最小生成树。基础类代码在上一课附录中,Kruskal算法函数代码在本棵附录中。

学思营编程课堂基于蓝桥STEM86平台https://www.stem86.com,开展学编程三部曲:
Scratch(三年级以前)>>>Python(四年级以后)>>>C++(七年级以后)教育实验活动,任何人可以免费参加,打开https://xuesiying.stem86.com网页注册进入课堂,也可关注本公众号留言。
更多课程请打开“学思营”同步网站:
http://www.5xstar.com/doc.html
参考资料:
1、Kruskal算法(克鲁斯卡尔算法)详解http://c.biancheng.net/algorithm/kruskal.html
2、《Python算法图解》何韬编著 清华大学出版社
附录1:
#邻接矩阵Kruskal最小生成树
from 最小生成树 import MinGraphTree
from 图结构_邻接矩阵 import GraphMatrix
#Kruskal算法
def matrixKruskal(gMat):
'''@gMat邻接矩阵图'''
lines = __getLines(gMat) #获取连线顺序表
result = None
value = None
starts = [] #已经完成的开始边
for i in range(len(lines)): #从0开始扫描起点,最小边数是大于0的偶数
if value == None: #获取最小值
value = lines[i][2]
starts.append(lines[i])
elif lines[i][2] > value: #如果最小边已完成
break
else:
if __checkStart(starts, lines[i]): #如果该边已经作为开始了,跳过
continue
else:
starts.append(lines[i])
lines[i], lines[0] = lines[0], lines[i] #交换最小边位置到第0位
reachedVertexList, parents, sumValue = __matrixKruskal(gMat, lines) #尝试一次
#print(i,reachedVertexList, parents, sumValue) #测试
if reachedVertexList != None: #找到一个解决方案
if result == None or sumValue < result[2]:
result = (reachedVertexList, parents, sumValue)
if result == None:
return None
else:
return MinGraphTree(result[0],result[1])
def __matrixKruskal(gMat, lines): #尝试lines[0]开始的最小树
line = lines[0] #取出0号
reachedVertexList = [line[0],line[1]] #已加的索引
parents = [None, line[0]] #父顶点索引
values = [0, line[2]] #权值
lines1 = lines[1:] #当次扫描
lines2 = [] # 下次扫描
while len(lines1)>0:
for lineIndex in range(len(lines1)):
line = lines1[lineIndex] #取出1边
(start, end, value) = line #解包一边
if end in reachedVertexList: #如果结束点已经在触达集,忽略
continue
elif start in reachedVertexList: #只开始端在已触达顶点
reachedVertexList.append(end) #把结束顶点加入触达集
parents.append(start) #把开始顶点加入父顶点集
values.append(value) #把权值加入权值集
if len(reachedVertexList) == gMat.length: #最小树生成成功
for i in range(gMat.length): #转换触达集
reachedVertexList[i] = (gMat.dict[reachedVertexList[i]],values[i])
for i in range(1,gMat.length): #转换parents, 第0个不用转换
parents[i] = gMat.dict[parents[i]]
return reachedVertexList, parents, sum(values) #返回方案
else: #还没完成
if lineIndex<len(lines1)-1: #没到最后一个元素,把剩下的元素
lines2.extend(lines1[lineIndex+1:]) #复制入下次扫描集中
break #中终止当次循环
else: #两点都不在触达集的元素放入下次扫描集中
lines2.append(line)
lines1 = lines2 #准备下次扫描
lines2 = []
return None,None,None
def __getLines(gMat): #获取连线顺序表
lines = [] #连线收集表
for i in range(gMat.length): #扫描矩阵,取出边
for j in range(gMat.length):
v = gMat.matrix[i][j]
if v > 0:
lines.append((i, j, v)) #加入一边
lines.sort(key=lambda line : line[2])
#key = lambda line : line[2] 相当于
#def fun(line):
# return line[2]
#key = fun
return lines
def __checkStart(starts, line): #检查是否已经在开始集中
for start in starts:
if start[0] == line[1] and start[1] == line[0]: #同一边
return True
return False
#测试 激发《五行星学编程》使用idle运行 input()
if __name__ == "__main__":
lst = ['A','B','C','D','S','T']
lstA = [['B',6],['C',3],['S',7]] #A连接B、C、S
lstB = [['C',4],['D',2],['T',5]] #B连接C、D、T
lstC = [['S',8],['D',3]] #C连接S、D
lstD = [['T',2]] #D连接T
gMat = GraphMatrix() #Kruskal算法只适用于无向图
for key in lst:
gMat.addVertex(key)
gMat.addLine(lst[0],lstA)
gMat.addLine(lst[1],lstB)
gMat.addLine(lst[2],lstC)
gMat.addLine(lst[3],lstD)
gMat.display()
print('------------------------')
mgTree = matrixKruskal(gMat) #转为最小生成树
if mgTree != None:
mgTree.display()
附录2:
#邻接表Kruskal最小生成树
from 最小生成树 import MinGraphTree
from 图结构_邻接表 import GraphList
#Kruskal算法
def listKruskal(gList):
'''@gList邻接表'''
lines = __getLines(gList) #获取连线顺序表
result = None
value = None
starts = [] #已经完成的开始边
for i in range(len(lines)): #从0开始扫描起点,最小边数是大于0的偶数
if value == None: #获取最小值
value = lines[i][2]
starts.append(lines[i])
elif lines[i][2] > value: #如果最小边已完成
break
else:
if __checkStart(starts, lines[i]): #如果该边已经作为开始了,跳过
continue
else:
starts.append(lines[i])
lines[i], lines[0] = lines[0], lines[i] #交换最小边位置到第0位
reachedVertexList, parents, sumValue = __listKruskal(gList, lines) #尝试一次
#print(i,reachedVertexList, parents, sumValue) #测试
if reachedVertexList != None: #找到一个解决方案
if result == None or sumValue < result[2]:
result = (reachedVertexList, parents, sumValue)
if result == None:
return None
else:
return MinGraphTree(result[0],result[1])
def __listKruskal(gList, lines): #尝试lines[0]开始的最小树
line = lines[0] #取出0号
reachedVertexList = [line[0],line[1]] #已加的键
parents = [None, line[0]] #父顶点键
values = [0, line[2]] #权值
lines1 = lines[1:] #当次扫描
lines2 = [] # 下次扫描
while len(lines1)>0:
for lineIndex in range(len(lines1)):
line = lines1[lineIndex] #取出1边
(start, end, value) = line #解包一边
if end in reachedVertexList: #如果结束点已经在触达集,忽略
continue
elif start in reachedVertexList: #只开始端在已触达顶点
reachedVertexList.append(end) #把结束顶点加入触达集
parents.append(start) #把开始顶点加入父顶点集
values.append(value) #把权值加入权值集
if len(reachedVertexList) == len(gList.dict): #最小树生成成功
for i in range(len(gList.dict)): #转换触达集
reachedVertexList[i] = (reachedVertexList[i],values[i])
return reachedVertexList, parents, sum(values) #返回方案
else: #还没完成
if lineIndex<len(lines1)-1: #没到最后一个元素,把剩下的元素
lines2.extend(lines1[lineIndex+1:]) #复制入下次扫描集中
break #中终止当次循环
else: #两点都不在触达集的元素放入下次扫描集中
lines2.append(line)
lines1 = lines2 #准备下次扫描
lines2 = []
return None,None,None
def __getLines(gList): #获取连线顺序表
lines = [] #连线收集表
for key in gList.dict: #扫描邻接表,取出边
row = gList.dict[key] #邻接表中一行
for (otherKey, value) in row:
lines.append((key, otherKey, value)) #加入一边
lines.sort(key=lambda line : line[2])
#key = lambda line : line[2] 相当于
#def fun(line):
# return line[2]
#key = fun
return lines
def __checkStart(starts, line): #检查是否已经在开始集中
for start in starts:
if start[0] == line[1] and start[1] == line[0]: #同一边
return True
return False
#测试 激发《五行星学编程》使用idle运行 input()
if __name__ == "__main__":
lst = ['A','B','C','D','S','T']
lstA = [['B',6],['C',3],['S',7]] #A连接B、C、S
lstB = [['C',4],['D',2],['T',5]] #B连接C、D、T
lstC = [['S',8],['D',3]] #C连接S、D
lstD = [['T',2]] #D连接T
gList = GraphList() #Kruskal算法只适用于无向图
for key in lst:
gList.addVertex(key)
gList.addLine(lst[0],lstA)
gList.addLine(lst[1],lstB)
gList.addLine(lst[2],lstC)
gList.addLine(lst[3],lstD)
gList.display()
print('------------------------')
mgTree = listKruskal(gList) #转为最小生成树
if mgTree != None:
mgTree.display()