观察下面的两对运算：
7+3=10，10-3=7；
7×3=21，21÷3=7。
四则运算都是双操作数（需要2个数来运算）的，加与减、乘与除是两对互逆的运行。一般情况逆运算用于求未知数：
x+3=10，x=10-3=7；
y×3=21，y=21÷3=7。
如果在乘法中的两个操作数相同：
y×y=81，
再也无法用乘法的逆运算——除法来求解y的值了。为了解决这个问题，这种自乘（同样的数相乘）的运算用乘方来表示。
aⁿ=b，n个相同因数乘积的运算，叫做乘方（aⁿ），乘方的结果（b）叫做幂(power)。其中，a叫做底数(base number)，n叫做指数(exponent)。aⁿ读作“a的n次幂”或“a的n次方”。上面的等式按乘方的定义可以写成：
y²=81，
读：y的2次方（或2次幂，或平方）等于81。
一个数都可以看作自己本身的一次方：
a1=a
指数1通常省略不写。在写分数和负数的n次方时要加括号，例如：
(-2)²，(
)²。
除了0以外的任何数的0次方均等于1：
a0=1（a≠0)。
乘方运算虽然有2个操作数，但没有操作符，比乘和除的优先级高（一定要注意了！）。
由于
9²=81和 (-9)²=81
相反的运算过程（逆运算）得到
y=9和y=-9。
我们把乘方的逆运算叫做开方。上面的指数是2，它的逆运算就是开二次方或开平方（extraction of square root）；如果指数是3，那逆运算是开三次方或开立方；其它情况只叫“开多少次方”。那开方的结果是怎样表示的呢？
一般地，如果一个正数x的平方等于a，即x²=a，那么这个正数x叫做a的算术平方根( arithmetic square root)。a的算术平方根记为
，读作“根号a”，a叫做被开方数( radicand)。
由上面的例子可以看到，一个正数开平方运算是一对相反数，为了能在一条式子中表示加或减运算及相反数结果，引入了±（加减号或正负号），这样81的开平方结果可以表示为：
y=±9。
容易发现，其中正的平方根就是算术平方根。为什么不直接叫正平方根，而叫算术平方根呢？这可能是历史原因造成，所谓的“根”就是解的意思，也许古时候不考虑负数，只求方程的正解，就叫这个正解平方根。现在为了区别，也为了继承历史就把正平方根叫做算术平方根。不要纠结正平方根和算术平方根名称上的差别，反正都是指一样的东西。先得出算术平方根，再取相反数就到全部的解（平方根）。
规定：0的算术平方根是0:
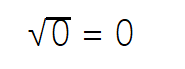
先看看平分东西的情况，例如2人平分3个苹果，每人分得
个苹果。3和2都是整数，但分得的苹果数不是整数，我们干脆把它的计算过程写下来当作结果，为了区分把÷号两点去掉，被除数写上面，除数写下面就成了分数。分数号的实质是除法，我们也用分数号当作除号来用。由于：
+
=3，
得到平分东西时，全部份的数量加起来等于总数。
类比一下，只考虑正数，可以认为开方是用乘法代替加法的平分数量操作，每份相乘起来等于总数（被开方数）。当被开方数不是有理数的乘方数（乘方次数等于开方次数），开方的结果就是一个无理数。无理数用小数的形式是无限位不循环小数，怎样表示它呢？用类似分数的方法吧！直接把运算符（开方号或根号）和被开方数写下来表示无理数。
一般情况，当被开方的是一个代数（例如：
）或无法被开方的数（例如：
），我们认为它表示一个无理数，否则认为是算术开方操作（当开方次数为偶数时，不考虑相反数），例如：
=2，不是√4=±2。
练习题：
1、一定能被计算机的二进制数准确记录的不大的数是（多选）：
（A）自然数 （B）整数 （C）有理数 （D）无理数 （F）实数
2、下面说法是否正确：
（A）自然数加自然数或自然数乘自然数一定是自然数；
（B）自然数减自然数一定是自然数；
（C）自然数除以非零自然数一定是自然数；
（D）整数减整数一定是整数；
（E）整数除以非零整数一定是整数；
（F）有理数除以非零有理数一定是有理数；
（G）无理数除以非零无理数一定是无理数；
（H）无理数加无理数一定是无理数；
（I）无理数减无理数一定是无理数；
（J）无理数乘无理数一定是无理数；
（K）非负有理数开方一定是有理数；
（L）非负实数开方一定是实数。
3、直接写出下面数的算术平方根：
（A）625 （B）169 （D）0.0144 （E）256 （F）0.0121
4、直接写出下面数的立方根：
（A）-27 （B）0.125 （D）-0.001 （E）64 （F）2
学Python时间：
1、乘方
方式有三种：
底数**指数；
pow(底数, 指数)；
import math后math.pow(底数, 指数)。
注意：计算2的3次方，前面2种结果是整数，后面一种结果是浮点数。
2、开方
与乘方对应，尝试连除号（//）：
连除号是整除号！
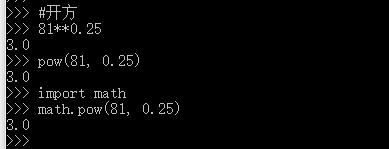
主要有三种方法：
被开方数**开方次数的倒数；
pow(被开方数, 开方次数的倒数)；
import math后math.pow(被开方数, 开方次数的倒数)。
开平方还有：
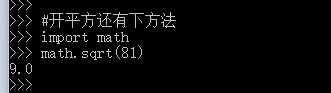
import math后math.sqrt(被开方数)
练习题：
用Python比较下面两个算式的大小：
然后提出你的猜想，尝试用数学方法证明你的猜想。（注：无次数根号是开平方）。