我们观察下面运算：

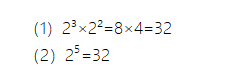
（1）式和（2）式的底都是2，3+2=5，不难发现同底幂乘法运算律：

同底幂的乘积等于同底指数和的幂。

这是个伟大的发现，因为把乘法转换为加法，使大数相乘简单化。

     看下面的运算：

2³÷2²=8÷4=2

由3-2=1，易得同底幂除法运算律：

同底幂的商等于同底指数差的幂。

幂的倒数：

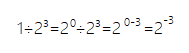
幂的倒数的运算规律：

幂的倒数是同底相反指数的幂。

    看下面运算：

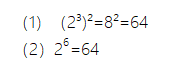
由3×2=6，可得镶套乘方运算规律：

镶套乘方等于底与各级指数积的幂。

    看下面的运算：

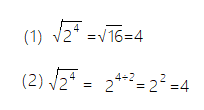
由4÷2=2，可得幂的开方（算术）运算规律：

幂的开方（算术）等于同底的指数除以开方次数的商的幂。

开方转乘方：

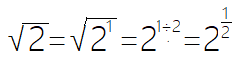
由1/2是2的倒数，得到开方（算术）转乘方的规律：

一个数的开方（算术）等于以被开方数为底的开方次数倒数的幂。

至此，你应该知道上一课的Python中，乘方和开方都使用pow函数和连乘号的缘故了吧！数学中随处可见——对立统一规律！

    看下面的运算：

可见，积、商和分数的幂运算分配律：

两个数积的幂等于两个数幂的积；

两个数商的幂等于两个数幂的商；

分数的幂等于分子幂和分母幂的分数。

练习题：已知a=2，求(a²×a³)³÷(a³÷a²)²的值。

​