我们看看下面的式子
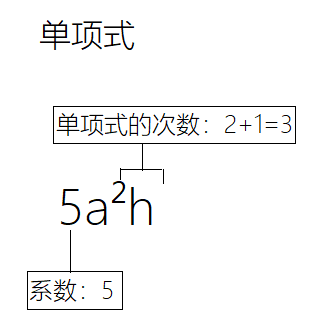
100t,0.8p,mn,5a²h,-n。
这些式子都是数或字母的积,像这样的式子叫做单项式( monomial)。单独的一个数或一个字母也是单项式。
单项式中的数字因数叫做这个单项式的系数( coefficient)。例如,单项式100t,5a²h,-n的系数分别是100,5,-1。单项式表示数与字母相乘时,通常把数写在前面。
一个单项式中,所有字母的指数的和叫做这个单项式的次数( degree of a monomial)。例如,在单项式100t中,字母t的指数是1,100t的次数是1;在单项式5a²h中,字母a与h的指数的和是3,5a²h的次数是3。
对于单独一个非零的数,规定它的次数为0。
我们再看下面式子
u+2.5,v-2.5,3x+5y+2z,1/2ab-Πr²,x²+2x+18。
这些式子都可以看作几个单项式的和。例如,v-2.5可以看作单项式v与-2.5的和;x²+2x+18可以看作单项式x²,2x与18的和。
像这样,几个单项式的和叫做多项式( polynomial)。其中,每个单项式叫做多项式的项(term),不含字母的项叫做常数项( constant term)。例如,多项式v-2.5的项是v与-2.5,其中-2.5是常数项;多项式x²+2x+18的项是x²,2x与18,其中18是常数项。
多项式里,次数最高项的次数,叫做这个多项式的次数( degree of a polynomial)。例如,多项式v-2.5中,次数最高项是一次项v,这个多项式的次数是1;多项式x²+2x+18中次数最高项是二次项x²,这个多项式的次数是2。

单项式与多项式统称整式( integral expression)。例如,上面见到的单项式100t,0.8p,mn,5a²h,-n,以及多项式u+2.5,v-2.5,3x+5y+2z,1/2ab-Πr²,x²+2x+18等都是整式。
像100t与—252t,3x²与2x²,3ab²与-4ab²这样,所含字母相同,并且相同字母的指数也相同的项叫做同类项。常数项都是同类项。
因为多项式中的字母表示的是数,所以我们也可以运用交换律、结合律、分配律把多项式中的同类项进行合并,例如,
4x²+2x+7+3x-8x²-2
=4x²-8x²+2x+3x+7-2 (交换律)
=(4x²-8x²)+(2x+3x)+(7-2) (结合律)
=(4-8)x²+(2+3)x+(7-2) (分配律)
=-4x²+5x+5。
把多项式中的同类项合并成一项,叫做合并同类。
项合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变。
约定俗成:通常我们把一个多项式的各项按照某个字母的指数从大到小(降幂)或者从小到大(升幂)的顺序排列,如-4x²+5x+5也可以写成5+5x-4x²。
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项。
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
注:如果括号外无因数,那因数式1或-1。
利用整式的运算法则,先去括号,再合并同类项,最后代入数值求值:

整式运算最好有验证过程:
如果变量有取值边界,就先验证边界,如果没有或已经验证边界,就取一个容易计算的值(一般是1)进行验证。例如,上一题取x=1,y=1验证,看看如何:
原式=1/2-2(1-1/3)+(-3/2+1/3)=1/2-2+2/3-3/2+1/3=-2,
结果式=-3+1=-2,
验证通过。
练习题:
1、化简并验证
(1)6(4a²b-ab²)-(2ab²+7a²b)
(2)(7a+5c+4b)+(8c-6b-5a)
(3)(10xy-2x²+2y²)-(2x²-2y²+10xy)
(4)(4x²-1/4+6x)-2(x-x²+1/4)
(5)5x²-[13x-(8x-2)-5x²]
2、化简、验证和求值
(1)(-2x²+10+8x)+(10x-8+4x²) 其中x=-3
(2)(4x²+1+4x)-(-2x-8+3x²) 其中x=2
3、根据描述写出整式并化简和验证
(1)比a的4倍大5的数与比a的3倍小2的数的和;
(2)比x的9倍大6的数与比x的5倍小7的数的差;
(3)某农场水稻种植面积是a(hm²),小麦种植面积是水稻种植面积的4倍,玉米种植面积比水稻种植面积少3(hm²),小麦种植面积比玉米种植面积大多少。注:hm²是square hectometer的缩写,平方公顷。
(4)门的形状如下图所示(图中长度单位:dm),其上部是半圆形,下部是边长相同的六个小正方形。已知下部小正方形的边长是a dm,门的面积和外框的总长。

(5)游轮在河中顺水航行3h,逆水航行1.5h,已知游轮在静水中的速度是a km/h,水流速度是b km/h,游轮船共航行的千米数。
(6)等腰梯形的上底是3b cm,下底是7b cm,腰是3b cm,n个这样的梯形腰与腰拼接成条状图像的周长。

(7)如下图,三角形周边填上点,从每边2个点开始,当每边填上n个点时,图型的点数。

(8)一个三位数,三个位上数字之和是10,百位的数字是a,十位的数字是百位的数字的三倍,写出这个数的多项式。
(9)9个棱长为p dm的正方体摆放成如下图的形状,这个图形的表面积。
