第一部分 整式相乘

一、单项式与单项式相乘

    利用乘法交换律、结合律及同底数幂的运算性质来计算：

单项式与单项式相乘，把它们的系数、同底数幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。

二、单项式与多项式相乘

    利用乘法分配律及单项式与单项式相乘的规律来计算：

单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加。

三、多项式与多项式相乘

    利用乘法分配律及单项式与多项式相乘的规律来计算。先把其中的一个多项式，如p+q，看成一个整体，运用单项式与多项式相乘的法则，得

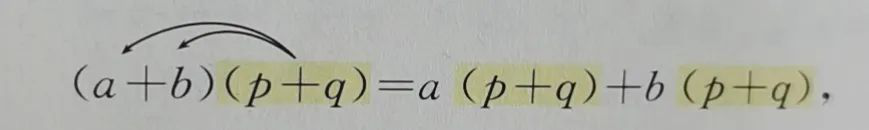
再利用单项式与多项式相乘的法则，得

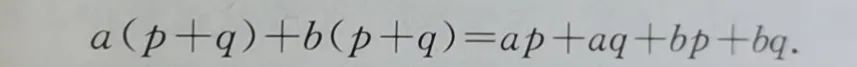总体上看，(a+b)(p+q)的结果可以看作由a+b的每一项乘p+q的每项，再把所得的积相加而得到的，即

    一般地，多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。

第二部分 整式相除

一、单项式与单项式相除

    单项式相除是单项式相乘的逆运算，一般地，把系数与同底数幂分别相除作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式：

二、多项式除以单项式

    多项式除以单项式，先把这个多项式的每一项除以这个单项式，再把所得的商相加：

(am+bm)÷m=am÷m+bm÷m=a+b

三、多项式相除

因为(x-1)(x²+x+1)=x³+x²+x-x²-x-1=x³-1

所以(x³-1)÷(x-1)=(x²+x+1)

    下图是用竖式进行计算：

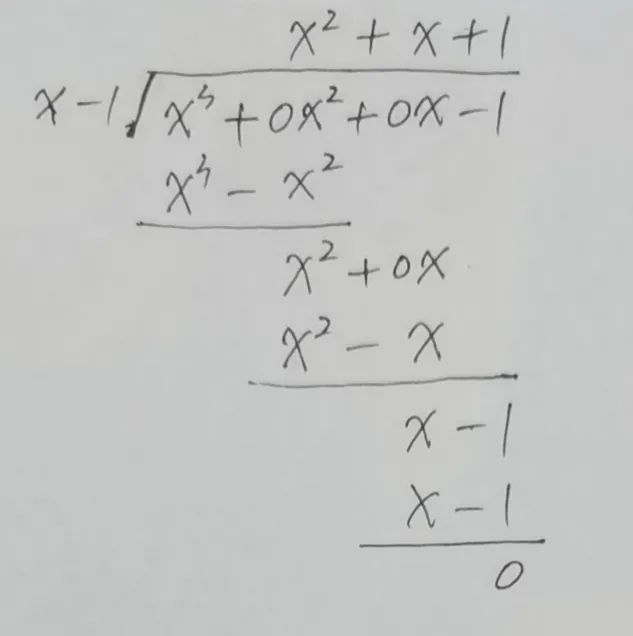
整式竖式除法类似于数的竖式除法，为了防止错误，当被除式和除式的次数有缺项时用系数是0的相应次数的项补齐。

练习题：计算（ · 表示乘号×）

（1）7y · (-4xy) 

（2）(3x-8y)(-5x)

（3）(x²+4x+5)(3x-7)

（4）-8a²b³÷6ab²   表示-8a²b³÷(6ab²）下同

（5）(17x²y-10xy²)÷5xy

（6）(x³+1)÷(x+1)

​