如果把整式乘法看作一个运算,那它的逆运算就是除法;如果把整式乘法看作一个过程,那它的逆过程就是因式分解(或分解因式,factorization)。因此,因式分解实际上就是正式除法的换一种说法。至于为什么要换一种说法,大概是便于用数学来分析现象的原因。
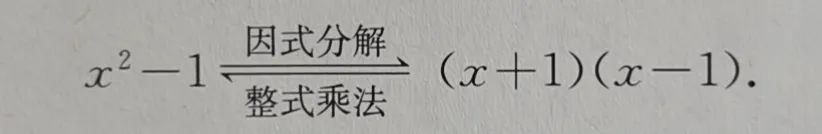
一、提公因式法
我们看多项式
pa+pb+pc,
它的各项都有一个公共的因式p,我们把因式p叫做这个多项式各项的公因式( common factor)。
由
p(a+b+c)=pa+pb+pc,
可得
pa+pb+pc=p(a+b+c)。
这样就把
pa+pb+pc
分解成两个因式乘积的形式,其中一个因式是各项的公因式p,另一个因式a+b+c是pa+pb+pc除以p所得的商。
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做“提公因式法”。
例1

例2
二、公式法
1、整式乘法的平方差公式
(a+b)(a-b)=a²-b²
的等号两边互换位置,就得到
a²-b²=(a+b)(a-b),
即两个数的平方差,等于这两个数的和与这两个数的差的积。
2、把整式乘法的完全平方公式
(a+b)²=a²+2ab+b²,
(a-b)²=a²-2ab+b²
的等号两边互换位置,就得到
a²+2ab+b²=(a+b)²,
a²-2ab+b²=(a-b)²,
即两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方。
三、解方程法(适合一元多项式)
不做一般描述,用例说明。把
x³-1
进行因式分解。
第一步,把整式变为方程:
x³-1=0;
第二步,解方程:
x³=1,
x=1;
第三步,构建因式:
x-1;
第四步,用竖式进行整式除法:

第五步,把除式与商式相乘作为结果:
x³-1=(x-1)(x²+x+1)。
注:如果商式还可以分解因式,需要继续分解。
四、x²+(p+q)x+pq型一元二次式因数分解法
我们发现
(x+p)(x+q)=x²+(p+q)x+pq
倒过来
x²+(p+q)x+pq=(x+p)(x+q)。
这个规律说明,只要把常数项分解为2个因数(注意正负号)的积,这两个因数的和等于一次项系数即可。
例如,分解因式
x²+3x+2,
2=1×2,1+2=3,
所以
x²+3x+2=(x+1)(x+2)。
五、abx²+(bp+aq)x+pq型一元二次式因数分解法
我们发现
(ax+p)(bx+q)=abx²+(bp+aq)x+pq
倒过来
abx²+(bp+aq)x+pq=(ax+p)(bx+q)。
这个规律说明,只要把二次项和常数项都分解为2个因数(注意正负号)的积,这两对因数交叉积
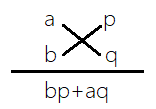
的和等于一次项系数即可。
例,分解因数
6x²+13x+2。
6=1×6,2=1×2,容易看到6×2+1×1=12+1=13,交叉式表示
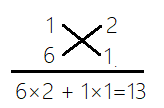 ,
,
可得
6x²+13x+2=(x+2)(6x+1)。
六、练习题
1、分解因式:
(1)24abc-8a²b²
(2)9a(x-y)-7b(y-x)
(3)-4x ²+9y²
(4)x²y-81y
(5)49a²-169b²
(6)-a^4+256 注:a^4表示a的4次方。
(7)36a²-b²/121
(8)16a²-8a+1
(9)ax²+6a²x+9a³
(10)x²-30x-99
(11)x²+15x-100
(12)12x²+41x+35
(13)15x+21x-18
(14)x³+27
(15)2x³-686
2、在实数范围内分解因式:
(1)3x³-2x
(2)x^4-4 注:x^4表示x的4次方
3、已知49x²+nxy+169y²是完全平方式,求n的值。
4、观察下面式子:
1×5+4=3²
2×6+4=4²
3×7+4=5²
7x11+4=9²
......
请用一个一元多项式表示这些等式,然后证明等式成立。
5、观察下面运算:
15×15=1×2×100+25=225,
25×25=2×3×100+25=625,
35×35=3×4×100+25=1225,
......
用一条一元整式的等式表示,并证明。
6、发现规律
(1)计算下列两个数的积(这两个数的十位上的数相同,个位上的数的和等于10),你发现结果有什么规律?
53×57,38×32,84×86,71×79
(2)你能用本章所学知识解释这个规律吗?
(3)利用你发现的规律计算:
58×52,63×67,75²,95²
七、Python学习时间
用Python实现x²+(p+q)x+pq型一元二次式因数分解法。
Python代码:
#x²+(p+q)x+pq型一元二次式因数分解法
#检查是否通过,如果通过就打印,返回True
def checkAndPrint(p_q, pq, sym, p, q):
if sym > 0:
if p_q > 0:
if p_q == p + q:
print("x²+%dx+%d=(x+%d)(x+%d)" %(p_q, pq, p, q))
return True
else:
if -p_q == p + q:
print("x²-%dx+%d=(x-%d)(x-%d)" %(-p_q, pq, p, q))
return True
else:
if p_q > 0:
if p_q == abs(p - q):
if p > q:
print("x²+%dx-%d=(x+%d)(x-%d)" %(p_q, pq, p, q))
else:
print("x²+%dx-%d=(x-%d)(x+%d)" %(p_q, pq, p, q))
return True
else:
if -p_q == abs(p - q):
if p > q:
print("x²-%dx-%d=(x-%d)(x+%d)" %(-p_q, pq, p, q))
else:
print("x²-%dx-%d=(x+%d)(x-%d)" %(-p_q, pq, p, q))
return True
return False
while True:
#一次系数
p_plus_q = int(input("请输入一次项系数,输入0退出:"))
if p_plus_q == 0:
break
#常数项
p_multiply_q = int(input("请输入常数项,输入0退出:"))
if p_multiply_q == 0:
break
#常数项因数分解
symbol = 1 #符号,1表示同正负号,-1表示正负号不同
if p_multiply_q < 0:
symbol = -1 #因数符号不同
p_multiply_q = -p_multiply_q #相反数,为正数
#检查1和本身
if checkAndPrint(p_plus_q, p_multiply_q, symbol, 1, p_multiply_q):
continue
maxTestNum = p_multiply_q//2 #除了数的本身,最大可能因数
lst = [(1,p_multiply_q)] #因数表,不含符号,初始值是1和本身
#查找其它因数对
hasFinded = False #是否发现
for n in range(2, maxTestNum+1):
if p_multiply_q % n == 0:
m = p_multiply_q // n #与n对应的因数
finished = False #是否已经完成
for temp in lst: #顺序检查
if temp[0] == m: #查找结束
finished = True #开完成开关
break #跳出内循环
if finished:
break #跳出外循环
lst.append((n, m)) #添加一对因数
print(lst) #打印因数分解列表
if checkAndPrint(p_plus_q, p_multiply_q, symbol, n, m): #检查
hasFinded = True #设置成功变量
break #退出内循环
#打印不可分解
if not hasFinded:
if symbol > 0:
if p_plus_q > 0:
print("x²+%dx+%d不能分解因式!" %(p_plus_q, p_multiply_q))
else:
print("x²-%dx+%d不能分解因式!" %(-p_plus_q, p_multiply_q))
else:
if p_plus_q > 0:
print("x²+%dx-%d不能分解因式!" %(p_plus_q, p_multiply_q))
else:
print("x²-%dx-%d不能分解因式!" %(-p_plus_q, p_multiply_q))
运行结果:

练习:建py文件,把代码考进去,运行,测试较大系数整式。