Python在标准模块fractions中的Fraction对象能实现分数,很贴心的数学功能,不懂就亏大了!下面就对这个分数对象进行介绍,不懂Python的人也可以按照例题的方法实现分数计算。
导入分数对象:
>>> from fractions import Fraction
实现一个整数:
>>> Fraction(123)
Fraction(123, 1)
>>> Fraction(-123)
Fraction(-123, 1)
实现一个分数:
>>> Fraction(16, 10)
Fraction(8, 5)
>>> Fraction(16, -10)
Fraction(-8, 5)
>>> Fraction('3/7')
Fraction(3, 7)
>>> Fraction(' -3/7 ') #引号内空格包括制表或换行不影响分数构建
Fraction(-3, 7)
小数变分数:
>>> Fraction('1.1') #注意要用引号把小数括起来
Fraction(11, 10)
>>> Fraction('1.414213 \t\n') #引号内空格包括制表或换行不影响分数构建
Fraction(1414213, 1000000)
>>> Fraction('-.125') #没有整数部分,小数点前的0可以省略
Fraction(-1, 8)
整数和分数的四则运算:
>>> Fraction(1, 2) + Fraction(1, 3) #分数加分数
Fraction(5, 6)
>>> Fraction(1, 2) - Fraction(1, 3) #分数减分数
Fraction(1, 6)
>>> 1 + Fraction(1, 3) #整数加分数
Fraction(4, 3)
>>> 1 - Fraction(1, 3) #整数减分数
Fraction(2, 3)
>>> Fraction(1, 3) - 1 #分数减整数
Fraction(-2, 3)
>>> Fraction(1, 2) * Fraction(1, 3) #分数乘分数
Fraction(1, 6)
>>> Fraction(1, 2) / Fraction(1, 3) #分数除分数
Fraction(3, 2)
>>> 2 * Fraction(1, 3) #整数乘分数
Fraction(2, 3)
>>> 2 / Fraction(1, 3) #整数除分数
Fraction(6, 1)
>>> Fraction(1, 3) / 2 #分数除以整数
Fraction(1, 6)
>>> Fraction(4) / 2
Fraction(2, 1)
>>> Fraction(1) * 1
Fraction(1, 1)
>>> Fraction(1) + Fraction(1)
Fraction(2, 1)
>>> Fraction(2) - Fraction(1)
Fraction(1, 1)
总结:整数与分数(不管是真分数还是假分数)的四则运算都是分数。
小数(浮点数)与分数的四则运算:
>>> 0.25 * Fraction(4)
1.0
>>> 0.25 + Fraction(3, 4)
1.0
>>> 0.25 - Fraction(1, 4)
0.0
>>> 0.25 / Fraction(1, -4)
-1.0
>>> Fraction('0.25') * Fraction(4)
Fraction(1, 1)
>>> Fraction('0.25') + Fraction(3, 4)
Fraction(1, 1)
>>> Fraction(' 0.25 ') - Fraction(1, 4)
Fraction(0, 1)
>>> Fraction('0.25') / Fraction(1, -4)
Fraction(-1, 1)
总结:小数(浮点数)与分数的四则运算都是小数(浮点数),要把小数转为分数才能得到分数的结果。
分数乘方运算:
>>> Fraction(1, 3) ** 2
Fraction(1, 9)
>>> pow(Fraction(1, 3), 2)
Fraction(1, 9)
>>> Fraction(1, 3) ** -2
Fraction(9, 1)
>>> pow(Fraction(1, 3), -2)
Fraction(9, 1)
#总结:分数的整数幂,结果为分数
>>> 2 ** Fraction(1, 2)
1.4142135623730951
>>> pow(2, Fraction(1, 2))
1.4142135623730951
>>> 4 ** Fraction(1, 2)
2.0
>>> pow(4, Fraction(1, 2))
2.0
>>> 2 ** -Fraction(1, 2)
0.7071067811865476
>>> 2 ** Fraction(-1, 2)
0.7071067811865476
>>> 2 ** Fraction(1, -2)
0.7071067811865476
>>> Fraction(1, 4) ** Fraction(1, 2)
0.5
>>> Fraction(1, 4) ** Fraction(3, 2)
0.125
#总结:整数和分数的真分数和带分数幂,结果为浮点数。
>>> 2 ** Fraction(2)
4
#总结:整数的分数形式正整数幂,结果为整数。
>>> 2 ** Fraction(-2)
Fraction(1, 4)
>>> 2 ** -2 #不用假分数的负整数幂,结果为浮点数
0.25
#总结:整数的分数形式负整数幂,结果为分数。
乘方运算总结:指数是真分数或带分数,结果是浮点数,其它情况是分数或整数。
分数算式的规律:只要避免在指数位置出现真分数或带分数,就能避免浮点数的出现。
例题,计算:
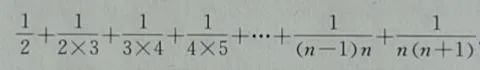
程序代码:

运行结果:

结果与上节课得到的计算公式相符。
练习题,用Python的分数对象计算,然后用上节课练习得到的公式验证: