

上节我们知道方向和距离可以确定点的坐标,反过来,两点的坐标也可以确定它们的距离。容易想到,这实际是知道直角三角形的直角边求斜边。用勾股定理:
直角边a和b,斜边c,
a²+b²=c²,
进行计算。
例题:已知A(-2,6)和B(6,-4),计算它们的距离(结果用最简根式表示)。用海龟画图标出A和B,并编写程序计算它们的距离核对你的结果。
分析:其中的直角三角形两直角边是x,y坐标的分别差,根据勾股定理,它们的平方和是两点距离的平方,开方化最简分数。编程的步骤也一样,只不过需要用到已经做好的二次根式计算模块和根式书写模块。
解:[6-(-2)]²+(-4-6)²=8²+10²=164,164开方=2根号41。
Python源程序代码(图片):


Python源程序代码(源码):
见附录1。
绘制出的精美图片:
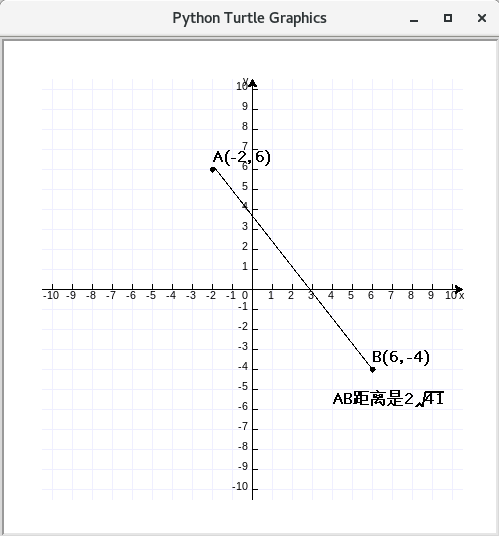
结论:计算值与程序的结果一致。
练习题:
三角形的三个顶点的坐标分别是A(-6,-8)、B(-3,2)、C(4,-4),求三角形的三边长度。仿上面的例题,画出这个三角形,标注顶点坐标,计算边长的实数值并打印在图上。
附录1:
#从两点的坐标计算两点的实数距离
import sys
sys.path.append("/5xstar/pyfiles") #预制自定义模块(py文件)存放根目录
import turtle as t #导入海龟画图
t.setup(500,500)
t.screensize(420,420)
t.shape("circle")
t.shapesize(0.25,0.25) #印章时是四分之一大小
from mymath.rcs import * #导入函数轨迹模块
from mymath.quadraticradical import QR #导入单项根式
from mymath.rooting import writeSqrt #导入根式书写函数
xUnt = (1,20) #数值与像素数值比例1:20,实际坐标是像素数的二十分之一
yUnt = (1,20)
build(t,xUnt,yUnt) #画平面直角坐标系
t.up()
workFont=("宋体", 12, "bold") #标位置字体:12号,宋体,黑体
#标定位置
def indication(name,pos,dx=2,dy=2,algn=None):
'''
@name 位置名称
@pos 位置坐标
@dx 写字位置x增加值
@dy 写字位置y增加值
@align 写字方向:center,left,right
'''
t.setpos(pos)
t.stamp()
t.setpos(pos[0]+dx,pos[1]+dy)
if algn == None:
t.write("%s(%d,%d)" % (name, pos[0]//20, pos[1]//20), font=workFont) #实际坐标是像素数的二十分之一
else:
t.write("%s(%d,%d)" % (name, pos[0]//20, pos[1]//20), align=algn, font=workFont)
ax, ay = -2, 6 #A点
t.setpos(ax*20,ay*20)
t.stamp()
indication("A",t.pos()) #打名称坐标
t.down()
bx, by = 6, -4 #B点
t.setpos(bx*20, by*20)
t.stamp()
indication("B",t.pos()) #打名称坐标
t.up()
t.sety((by-2)*20) #打印结果
qr=QR(1, (bx-ax)**2+(by-ay)**2)
t.write("AB距离是%s" % str(qr.coefficient), move=True, align="center", font=workFont) #打印根号前系数
if qr.bottom != 1:
writeSqrt(t, qr.bottom, font=workFont)
t.ht()
t.mainloop()
附录2:
'''初中平面直角坐标系中单值函数轨迹、画直线和打点
@作者 码老师
@微信公众号 学思营 ID:xuesying
@公司 深圳五行星软件有限公司
@日期 2020-12-19
@使用方法
1、导入海龟画图并初始化窗口和画布,例如:
import turtle as t
t.setup(600,600)
t.screensize(400,400)
t.shape("turtle")
2、导入本模块:
from rcs import *
3、用下面函数:
build(aTurtle, xUnt = None, yUnt = None, wc = None):
@aTurtle 一个海龟
@xUnt x轴数值与像素对应元组
@yUnt y轴数值与像素对应元组
@wc 自定义坐标元组(llx, lly, urx, ury)
@llx -- 一个数值, 画布左下角的 x-坐标(像素)
@lly -- 一个数值, 画布左下角的 y-坐标
@urx -- 一个数值, 画面右上角的 x-坐标
@ury -- 一个数值, 画布右上角的 y-坐标
画平面直角坐标系,例如:
build(t) #, worldcoordinates=(0,0,400,400))
4、使用模块进行画单调函数轨迹、直线和打点
(1)画函数轨迹
第一步:定义一个单调函数例如:
def fun(x):
return 5*x + 3
第二步:获取x,y的取值范围:
minx, maxx, miny, maxy = getRange()
第三步(可选):根据x,y的取值范围和函数的实际要求,确定自变量取值范围:
x1,x2
第四步:调用下面函数:
trace(aTurtle, x1, x2, fun):
@aTurtle 一个海龟
@x1 自变量一端点值
@x2 自变量另一端点值
@fun 单调函数
画函数轨迹,例如:
#一元一次函数
def fun(x):
return 2*x + 1
trace(t, 50, -50, fun)
(2)画直线段
第一步:获取x,y的取值范围:
minx, maxx, miny, maxy = getRange()
第二步:调用下面函数:
line(aTurtle, x1, y1, x2, y2):
@aTurtle 一个海龟
@x1,y1 始点
@x2,y2 终点
画直线段,例如画对角线:
line(t, minx, miny, maxx, maxy)
(3)打圆点
第一步:获取x,y的取值范围:
minx, maxx, miny, maxy = getRange()
第二步:调用下面函数:
circularDot(aTurtle, x, y, size=None, *color):
@aTurtle 一个海龟
@x,y 坐标
@size 圆点大小
@color 圆点颜色
打圆点,例如下降对角线打点:
x, y = minx, maxy
size = 1
while True:
if x > maxx or y < miny:
break
circularDot(t, x, y, size, "red")
x += 1
y -= 1
size += 1
'''
#导入分数
from fractions import Fraction
#坐标轴线宽
axisWidth = 1
#坐标轴和坐标点颜色
axisColor = "black"
#坐标箭头
axisTurtle = "classic"
#箭头大小 原来四分之一 轮廓线1
axisShapesize = (0.8, 0.8, 1)
#数轴单位(整数)及其对应的像素大小(整数) 1对应10像素
xUnit = [1, 20]
yUnit = [1, 20]
#方格线宽
squareWidth = 1
#方格线色 浅蓝
squareColor = "#EFEFFF"
#数点线长
markLen = 5
#数字字体
markFont=("Arial", 8, "normal")
#坐标系,调用build后才有值
worldcoordinates = None
#检测数轴单位
def __checkUnit(unt):
if unt != None and len(unt) == 2:
return isinstance(unt[0],int) and isinstance(unt[0],int)
return False
#建立直角坐标系
def build(aTurtle, xUnt = None, yUnt = None, wc = None):
'''按初中课本使用的直角坐标系绘图
@aTurtle 一个海龟
@xUnt x轴数值与像素对应元组
@yUnt y轴数值与像素对应元组
@wc 自定义坐标元组(llx, lly, urx, ury)
@llx -- 一个数值, 画布左下角的 x-坐标(像素)
@lly -- 一个数值, 画布左下角的 y-坐标
@urx -- 一个数值, 画面右上角的 x-坐标
@ury -- 一个数值, 画布右上角的 y-坐标'''
#保持海龟原来的参数后设置参数
speed = aTurtle.speed()
aTurtle.speed(0)
width = aTurtle.pensize()
pencolor = aTurtle.pencolor()
shape = aTurtle.shape()
shapesize = aTurtle.shapesize()
isdown = aTurtle.isdown()
pos = aTurtle.pos()
heading =aTurtle.heading()
#数量与像素的对应关系
if __checkUnit(xUnt):
xUnit[0] = xUnt[0]
xUnit[1] = xUnt[1]
if __checkUnit(yUnt):
yUnit[0] = yUnt[0]
yUnit[1] = yUnt[1]
global worldcoordinates
#自定义坐标
if wc != None and len(wc) == 4:
worldcoordinates = wc
aTurtle.setworldcoordinates(*worldcoordinates) #自定义坐标系
else:
temp = aTurtle.screensize()
worldcoordinates = (-temp[0]/2,-temp[1]/2,temp[0]/2,temp[1]/2)
#定坐标方向
xh = worldcoordinates[0] < worldcoordinates[2]
if xh: #True从左到右
x1,x2 = int(worldcoordinates[0]), int(worldcoordinates[2])
else:
x1,x2 = int(worldcoordinates[2]), int(worldcoordinates[0])
yh = worldcoordinates[1] < worldcoordinates[3]
if yh: #True从下到上
y1,y2 = int(worldcoordinates[1]), int(worldcoordinates[3])
else:
y1,y2 = int(worldcoordinates[3]), int(worldcoordinates[1])
#画方格线
#画与y轴平行的线
if isdown:
aTurtle.up()
for i in range(-xUnit[1], x1, -xUnit[1]):
aTurtle.pencolor(squareColor)
aTurtle.pensize(squareWidth)
aTurtle.setpos(i,y1)
aTurtle.down()
aTurtle.sety(y2)
aTurtle.up()
aTurtle.sety(0)
aTurtle.down()
aTurtle.pencolor(axisColor)
aTurtle.pensize(axisWidth)
aTurtle.sety(markLen)
aTurtle.up()
if yh: #标x数字
aTurtle.sety(-markLen-markFont[1]) #还要下降字体高度
else:
aTurtle.sety(-markLen//2) #无需下降字体高度
aTurtle.write(i//xUnit[1]*xUnit[0], align="center", font = markFont)
for i in range(xUnit[1], x2, xUnit[1]):
aTurtle.pencolor(squareColor)
aTurtle.pensize(squareWidth)
aTurtle.setpos(i,y1)
aTurtle.down()
aTurtle.sety(y2)
aTurtle.up()
aTurtle.sety(0)
aTurtle.down()
aTurtle.pencolor(axisColor)
aTurtle.pensize(axisWidth)
aTurtle.sety(markLen)
aTurtle.up()
if yh:
aTurtle.sety(-markLen-markFont[1])
else:
aTurtle.sety(-markLen//2)
aTurtle.write(i//xUnit[1]*xUnit[0], align="center", font = markFont)
#画与x轴平行的线
for i in range(-yUnit[1], y1, -yUnit[1]):
aTurtle.pencolor(squareColor)
aTurtle.pensize(squareWidth)
aTurtle.setpos(x1, i)
aTurtle.down()
aTurtle.setx(x2)
aTurtle.up()
aTurtle.setx(0)
aTurtle.down()
aTurtle.pencolor(axisColor)
aTurtle.pensize(axisWidth)
aTurtle.setx(markLen)
aTurtle.up()
if yh: #标y数字
aTurtle.setpos(-markLen//2, i-markFont[1]//2) #下降字体高度一半
else:
aTurtle.setpos(-markLen//2, i+markFont[1]//2)
if xh:
aTurtle.write(i//yUnit[1]*yUnit[0], align="right", font = markFont)
else:
aTurtle.write(i//yUnit[1]*yUnit[0], font = markFont)
for i in range(yUnit[1], y2, yUnit[1]):
aTurtle.pencolor(squareColor)
aTurtle.pensize(squareWidth)
aTurtle.setpos(x1, i)
aTurtle.down()
aTurtle.setx(x2)
aTurtle.up()
aTurtle.setx(0)
aTurtle.down()
aTurtle.pencolor(axisColor)
aTurtle.pensize(axisWidth)
aTurtle.setx(markLen)
aTurtle.up()
if yh:
aTurtle.setpos(-markLen//2, i-markFont[1]//2)
else:
aTurtle.setpos(-markLen//2, i+markFont[1]//2)
if xh:
aTurtle.write(i//yUnit[1]*yUnit[0], align="right", font = markFont)
else:
aTurtle.write(i//yUnit[1]*yUnit[0], font = markFont)
#画坐标
aTurtle.pencolor(axisColor)
aTurtle.pensize(axisWidth)
aTurtle.shape(axisTurtle)
aTurtle.shapesize(*axisShapesize)
aTurtle.up()
aTurtle.setpos(x1, 0)
aTurtle.down()
aTurtle.setx(x2)
if xh:
aTurtle.seth(0)
else:
aTurtle.seth(180)
aTurtle.stamp()
aTurtle.up()
if yh:
aTurtle.sety(-markLen-markFont[1])
else:
aTurtle.sety(-markLen//2)
aTurtle.write('x', align="center", font = markFont)
aTurtle.setpos(0, y1)
aTurtle.down()
aTurtle.sety(y2)
if yh:
if xh:
aTurtle.seth(90)
else:
aTurtle.seth(-90)
else:
if xh:
aTurtle.seth(90)
else:
aTurtle.seth(-90)
aTurtle.stamp()
aTurtle.up()
if yh:
aTurtle.setpos(-markLen//2, y2-markFont[1])
else:
aTurtle.setx(-markLen//2)
if xh:
aTurtle.write('y', align="right", font = markFont)
else:
aTurtle.write('y', font = markFont)
#标注原点
if yh:
aTurtle.setpos(-markLen//2, -markLen-markFont[1])
else:
aTurtle.setpos(-markLen//2, -markLen//2)
if xh:
aTurtle.write(0, align="right", font = markFont)
else:
aTurtle.write(0, font = markFont)
#恢复海龟原来的设置参数
aTurtle.speed(speed)
aTurtle.shape(shape)
aTurtle.pensize(width)
aTurtle.pencolor(pencolor)
aTurtle.shapesize(*shapesize)
aTurtle.setpos(*pos)
aTurtle.seth(heading)
if isdown:
aTurtle.down()
#检查是否已经初始化
def __checkBuild():
if worldcoordinates == None:
print("还没有画坐标,请调用build(aTurtle, xUnt = None, yUnt = None, worldcoordinates = None)函数画坐标")
return False
else:
return True
#屏幕上进1像素实际的值之间的转换
def __pixchange():
#屏幕上进1像素实际的值之间的转换
dx, udx, dy, udy = Fraction(*xUnit), Fraction(xUnit[1], xUnit[0]), Fraction(*yUnit), Fraction(yUnit[1], yUnit[0])
#x坐标作图范围
if worldcoordinates[0] < worldcoordinates[2]:
minx, maxx = dx * worldcoordinates[0], dx * worldcoordinates[2]
else:
minx, maxx = dx * worldcoordinates[2], dx * worldcoordinates[0]
#y坐标作图范围
if worldcoordinates[1] < worldcoordinates[3]:
miny, maxy = dy * worldcoordinates[1], dy * worldcoordinates[3]
else:
miny, maxy = dy * worldcoordinates[3], dy * worldcoordinates[1]
return dx, udx, dy, udy, minx, maxx, miny, maxy
#函数轨迹
def trace(aTurtle, x1, x2, fun):
'''函数轨迹
@aTurtle 一个海龟
@x1 自变量一端点值
@x2 自变量另一端点值
@fun 单调函数'''
#自变量检查
if x1 == x2:
print("自变量不可以相等")
return False
#检查是否已经画坐标
if not __checkBuild():
return False
#保持海龟落笔状态
isdown = aTurtle.isdown()
speed = aTurtle.speed()
aTurtle.speed(0)
pos = aTurtle.pos()
if isdown:
aTurtle.up()
if x1 > x2: #交换自变量
temp = x1
x1 = x2
x2 = temp
#屏幕上进1像素实际的值之间的转换
dx, udx, dy, udy, minx, maxx, miny, maxy = __pixchange()
if x2 <= minx or x1 >= maxx:
print("自变量不在%s到%s范围内!" % (str(minx), str(maxx)))
return False
if x1 < minx:
x1 = minx
if x2 > maxx:
x2 = maxx
#起点
x = x1
y = fun(x1)
if y >= miny and y<= maxy:
aTurtle.setpos(udx*x, udy*y)
aTurtle.down()
#描图
while True:
x += dx
if x > x2: #过了终点
break
y = fun(x)
if y >= miny and y<= maxy:
aTurtle.setpos(udx*x, udy*y)
if not aTurtle.isdown():
aTurtle.down()
else:
if aTurtle.isdown():
aTurtle.setpos(udx*x, udy*y)
aTurtle.up()
if aTurtle.isdown():
aTurtle.up()
aTurtle.setpos(*pos)
aTurtle.speed(speed)
#恢复下笔状态
if isdown:
aTurtle.down()
return True
#作图范围
def getRange():
'''作图范围
@return x坐标最小值,x坐标最大值,y坐标最小值,y坐标最大值'''
#检查是否已经画坐标
if not __checkBuild():
return None
#屏幕上进1像素实际的值之间的转换
dx, udx, dy, udy, minx, maxx, miny, maxy = __pixchange()
return minx, maxx, miny, maxy
#作图范围字符串
def __rangestr(minx, maxx, miny, maxy):
return "%s≤x≤%s,%s≤y≤%s" % (str(minx),str(maxx),str(miny),str(maxy))
#画线段
def line(aTurtle, x1, y1, x2, y2):
'''画线段
@aTurtle 一个海龟
@x1,y1 始点
@x2,y2 终点'''
#检查是否已经画坐标
if not __checkBuild():
return False
#屏幕上进1像素实际的值之间的转换
dx, udx, dy, udy, minx, maxx, miny, maxy = __pixchange()
if min(x1, x2) < minx or max(x1, x2) > maxx or min(y1, y2) < miny or max(y1, y2) > maxy:
print("有端点不在作图范围(%s)内!" % __rangestr(minx, maxx, miny, maxy))
return False
#保持海龟落笔状态
isdown = aTurtle.isdown()
pos = aTurtle.pos()
speed = aTurtle.speed()
aTurtle.speed(0)
if isdown:
aTurtle.up()
aTurtle.setpos(udx*x1, udy*y1)
aTurtle.down()
aTurtle.setpos(udx*x2, udy*y2)
aTurtle.up()
aTurtle.setpos(*pos)
aTurtle.speed(speed)
if isdown:
aTurtle.down()
return True
#打圆点
def circularDot(aTurtle, x, y, size=None, *color):
'''打点
@aTurtle 一个海龟
@x,y 坐标
@size 圆点大小
@color 圆点颜色'''
#检查是否已经画坐标
if not __checkBuild():
return False
#屏幕上进1像素实际的值之间的转换
dx, udx, dy, udy, minx, maxx, miny, maxy = __pixchange()
if x< minx or x > maxx or y < miny or y > maxy:
print("该点点不在作图范围(%s)内!" % __rangestr(minx, maxx, miny, maxy))
return False
isdown = aTurtle.isdown()
pos = aTurtle.pos()
speed = aTurtle.speed()
aTurtle.speed(0)
if isdown:
aTurtle.up()
aTurtle.setpos(udx*x, udy*y)
if color == None:
aTurtle.dot(size)
else:
aTurtle.dot(size, *color)
aTurtle.setpos(*pos)
aTurtle.speed(speed)
if isdown:
aTurtle.down()
return True
if __name__ == "__main__":
import turtle as t
t.setup(600,600)
t.screensize(400,400)
t.shape("turtle")
build(t) #, worldcoordinates=(0,0,400,400))
#一元一次函数
def fun1(x):
return 2*x + 1
trace(t, 50, -50, fun1)
#一元二次函数
def fun2(x):
return x**2 + 2*x + 2
trace(t, 50, -50, fun2)
#画圆
def fun3(x):
return (5**2 - x**2)**0.5
trace(t, 5, -5, fun3)
def fun4(x):
return -(5**2 - x**2)**0.5
trace(t, 5, -5, fun4)
#画对角线
minx, maxx, miny, maxy = getRange()
line(t, minx, miny, maxx, maxy)
#打点对角线
x, y = minx, maxy
size = 1
while True:
if x > maxx or y < miny:
break
circularDot(t, x, y, size, "red")
x += 1
y -= 1
size += 1
t.mainloop()
附录3:
'''二次根式加、减、乘、除(除数项数不超过2)和乘方运算
@作者 码老师
@微信公众号 学思营 ID:xuesying
@公司 深圳五行星软件有限公司
@日期 2020-11-01
@使用方法
1、导入模块
>>>from quadraticradical import *
2、单项二次根
空单项二次根式(与0相等)例如:
>>>QR()
整数单项二次根式例如:
>>>QR(3)
分数单项二次根式例1:
>>>QR("1/2")
分数单项二次根式例2:
>>>from fractions import Fraction
>>>QR(Fraction(1, 2))
小数单项二次根式(字符串输入,系统自动转为分数):
>>>QR("3.14")
如果单项二次根式有根号数,底数在常数之后,例如
>>>QR("3.14", 10)
3、多项二次根式
空多项二次根式(与0相等):
>>>pr = PR()
>>>pr.pt()
可以有列表化单项二次根式,单项二次根式和多项二次根式参数,例如:
>>>q1 = QR("3.14", 2)
>>>p1 = PR([12, 98])
>>>_test = PR(q1, p1, QR("2/3", 10), PR(q1, [9, 8]), ["5/3", 20])
>>>_test.pt()
4、加多项二次根式:
>>>_test.add(["2.5", 3], PR(["7.5", 18])).pt()
5、减多项二次根式:
>>>_test.sub(PR(["3/2",32], ["3/4",20])).pt()
6、乘多项二次根式:
>>>_test.mul([1,30],[1]).pt()
7、除以常数:
>>>_test.div("-1/2").pt()
8、除以单项二次根式:
>>>_test.div(["1/2","1/10"]).pt()
9、除以二项二次根式:
>>>_test.div(["1/2","1/10"], ["0.125", "3.75"]).pt()
10、乘方:
>>>PR([1,3],[1,2]).pow(5).pt()
'''
import math
from fractions import Fraction
#二次方根数类
class QR:
'''quadratic radical'''
coefficient = 0 #系数 有理数
bottom = 1 #方根的底——非负有理数
#相反数
def opp(self):
if self.coefficient != None:
self.coefficient = -self.coefficient
return self
#倒数
def rec(self):
self.coefficient = Fraction(1, self.coefficient * self.bottom)
return self
#克隆
def clone(self):
return QR(self.coefficient, self.bottom)
#打印
def print(self, isFirst):
if self.coefficient == None or self.coefficient == 0 or self.bottom == None or self.bottom == 0:
return ""
else:
if self.coefficient == 1:
s = ""
elif self.coefficient == -1:
s = "-"
else:
s = str(self.coefficient)
if self.coefficient > 0:
if not isFirst:
s = "+" + s
if self.bottom != 1:
s += "sqrt(%d)" % self.bottom
return s
#比较大小:底降序
#第二个要在前正值;合并0;其它负值
def cmp(pr, otherPr):
return otherPr.bottom - pr.bottom;
#初始化方法
def __init__(self, coefficient=0, bottom=1):
#print("coefficient=",coefficient,"bottom=",bottom)
if not isinstance(coefficient, (int, Fraction, str)) or not isinstance(bottom, (int, Fraction, str)):
raise ValueError("输入的不是整数、分数或字符串(小数、分数)!")
if isinstance(coefficient, (str)):
coefficient = Fraction(coefficient)
if isinstance(bottom, (str)):
bottom = Fraction(bottom)
if bottom < 0:
raise ValueError("底数不可以小于0!")
self.coefficient = coefficient
self.bottom = bottom
self.__simplestQuadraticRadical() #化简
#平方方法
def square(self):
return self.coefficient**2 * self.bottom
#描述自己
def __str__(self):
if self.coefficient == 0 or self.bottom == 0:
return "0"
if self.bottom == 1:
return str(self.coefficient)
return "%ssqrt(%s)" % (str(self.coefficient), str(self.bottom))
#化成最简二次根式
def __simplestQuadraticRadical(self):
#如果底是分数,就化为整数
if isinstance(self.bottom, (Fraction)):
self.coefficient = Fraction(self.coefficient, self.bottom.denominator)
self.bottom = self.bottom.numerator * self.bottom.denominator
return self.__firstStep()
#第一步:检测自己是否是平方数,如果是就变成整数
def __firstStep(self):
#print("第一步:检测自己是否是平方数")
tmp = round(math.sqrt(self.bottom)) #开方的最近整数
if tmp ** 2 == self.bottom:
self.coefficient *= tmp
self.bottom = 1
return self
return self.__secondStep()
#第二步:如果不是平方数,计算最大的可能因数
def __secondStep(self):
#print("第二步:如果不是平方数,计算最大的可能因数")
maxNum = self.bottom // 2
return self.__thirdStep(maxNum)
#第三步:寻找不大于最大的可能因数的最近平方数
def __thirdStep(self, maxNum):
#print("第三步:寻找不小于最大的可能因数的最近平方数")
end = math.ceil(math.sqrt(maxNum))
return self.__fourthStep(end)
#第四步:分解平方数的因数
def __fourthStep(self, end):
#print("第四步:分解平方数的因数")
factors = [] #平方数是self.intNum的因数的数
startNum = self.bottom #开始数
for i in range(end, 1, -1):
i2 = i ** 2
endNum = startNum // i2
if i2 * endNum == startNum:
factors.append(i)
startNum = endNum
return self.__fifthStep(factors, startNum)
#第五步:平方数因数开方成倍数,根式化成最简式
def __fifthStep(self, factors, startNum):
#print("第五步:平方数因数开方成倍数,根式化成最简式")
if len(factors) == 0:
return self #根式已经是最简根式
else:
self.coefficient *= self.__getCoefficient(factors)
self.bottom = startNum
return self
#根据因数的二次方根,生成最简根式的系数
def __getCoefficient(self, factors):
rst = 1
for f in factors:
rst *= f
return rst
#乘二次根式
def mul(self, otherQr):
self.coefficient *= otherQr.coefficient
self.bottom *= otherQr.bottom
return self.__simplestQuadraticRadical()
#多项二次根式
class PR:
'''多项quadratic radical'''
#项quadratic radical列表
terms = None
#克隆
def __clone(self):
p = PR()
if self.terms == None or len(self.terms) == 0:
return p
lth = len(self.terms)
t = []
for i in range(lth):
t.append(self.terms[i].clone())
p.terms = t
return p
#排序合并同类项,按底数从大到小
def __sort1(terms, idx, num):
term = terms[num] #需检查的元素
for i in range(idx+1): #把元素插入或合并到结果中
m = terms[i]
t = m.cmp(term) #比较
if t == 0: #合并同类项
m.coefficient += term.coefficient
return idx
elif t > 0: #新的高阶项,高阶项插入当前位置
idx += 1
for p in range(idx, i, -1): #后推其它项
terms[p] = terms[p-1]
terms[i] = term #插入该项
return idx #返回结果数
idx += 1
terms[idx] = term #把新项插在结果最后
return idx
#合并同类项与排序
def __sort(terms):
idx = 0 #结果下标
lth = len(terms)
for num in range(1, lth):
idx = PR.__sort1(terms, idx, num) #排序和合并1项
#print("idx=%d" % idx)
#消除0系数项
temp = []
for num in range(idx +1):
term = terms[num]
if term.coefficient != 0:
temp.append(term)
nlth = len(temp)
if nlth == 0:
del(terms[0:])
return terms
else:
for num in range(nlth):
terms[num] = temp[num]
if nlth < lth:
del(terms[nlth:])
return terms;
#打印自己
def __str__(self):
s = "原式="
if self.terms == None or len(self.terms) == 0:
s += "0"
else:
s += self.terms[0].print(True)
for i in range(1, len(self.terms)):
s += self.terms[i].print(False)
return s
def pt(self):
print(self)
#加
def __add(self, isSub, *terms):
if terms != None and len(terms) > 0:
if self.terms == None:
self.terms = []
for term in terms:
if isinstance(term, PR):
if term.terms != None and len(term.terms) > 0:
for t in term.terms:
if isSub:
self.terms.append(t.clone().opp()) #克隆,保证原式不受影响
else:
self.terms.append(t.clone())
else:
if isinstance(term, QR):
if isSub:
self.terms.append(term.clone().opp()) #克隆防止影响原对象
else:
self.terms.append(term.clone())
else:
if isSub:
self.terms.append(QR(*term).opp()) #解包list添加1个单项式,无需克隆
else:
self.terms.append(QR(*term))
PR.__sort(self.terms) #排序
def add(self, *terms):
s = self.__clone() #克隆防止改变原对象
s.__add(False, *terms)
return s
#减
def sub(self, *terms):
s = self.__clone() #克隆防止改变原对象
s.__add(True, *terms)
return s
#乘除常数,私有方法不克隆
def __muldiv(self, fraction, isdiv):
if self.terms != None and len(self.terms) >0:
if isinstance(fraction, (int, Fraction)):
p = fraction
else:
p = Fraction(fraction)
for term in self.terms:
if isdiv:
term.coefficient /= p
else:
term.coefficient *= p
return self
#多项乘单项,私有方法都不可以克隆
def __mul(pr, qr):
for term in pr.terms:
term.mul(qr)
PR.__sort(pr.terms) #排序
return pr
#乘
def mul(self, *terms):
if terms == None or len(terms) == 0: #空调用返回自己
return self
if len(terms) == 1 and isinstance(terms[0],(int, Fraction, str)): #乘一个有理数
return self.__clone().__muldiv(terms[0], False) #需要克隆对象
p = PR(*terms) #建立要乘的多项式 如果里面有Mn或Pn,则它们会被克隆
if self.terms == None or len(self.terms) == 0: #self是空多项式可忽略
return p
elif p.terms != None and len(p.terms) >0:
lth = len(p.terms)
s = self.__clone().__mul(p.terms[0]) #乘单项式
if lth == 1:
return s
for i in range(lth-1): #克隆对象乘
s.__add(False, self.__clone().__mul(p.terms[i+1]))
return s
else: #p为空多项式
return self;
#乘方
def pow(self, num):
if not isinstance(num, (int)) or num < 2:
print("请输入大于1的整数")
return self
if self.terms == None or len(self.terms) == 0:
return self
s = self.__clone()
for i in range(num-1):
s = s.mul(self) # 由于mul会克隆,这里不用克隆
return s
#2项式倒数,使用平方差公式
def __rec2(self):
d = self.terms[0].square() - self.terms[1].square() #分母
self.terms[1].opp() #第二项取相反数
return self.__muldiv(d, True)
#除
def div(self, *terms):
if terms == None or len(terms) == 0: #空调用返回自己
return self
if len(terms) == 1 and isinstance(terms[0],(int, Fraction, str)):
return self.__clone().__muldiv(terms[0], True)
pq = PR(*terms)
if pq.terms == None or len(pq.terms) == 0:
return self
elif len(pq.terms) == 1:
return self.__clone().__mul(pq.terms[0].rec())
elif len(pq.terms) == 2: #只处理2项式
return self.mul(pq.__rec2()) #2项式倒数
else:
raise ValueError("除数多项二次根式超过了2项,超出本模块处理范围!")
#构造
def __init__(self, *terms):
if terms == None or len(terms) > 0:
self.terms = []
for term in terms:
if isinstance(term, (QR)):
self.terms.append(term.clone())
elif isinstance(term, (PR)):
if term.terms != None and len(term.terms) > 0:
for t in term.terms:
self.terms.append(t.clone())
else:
self.terms.append(QR(*term)) #解包参数
PR.__sort(self.terms) #排序合并同类项,按底数从大到小
if __name__ == "__main__":
print("\n二次根式测试:")
print("\n导入二次根式模块:")
print('>>>from quadraticradical import *')
print("\n构造函数测试:")
print('>>>_qr = QR("3/2", 32)')
print('>>>_pr = PR(["3/5", 8])')
print('>>>_test = PR(["-3.14", 128], _qr, _pr, [4])')
print('>>>_test.pt()')
_qr = QR("3/2", 32)
_pr = PR(["3/5", 8])
_test = PR(["-3.14", 128], _qr, _pr, [4])
_test.pt()
print("对比")
print('>>>_test = PR(["-3.14", 128], ["3/2", 32], ["3/5", 8], [4])')
print('>>>_test.pt()')
_test = PR(["-3.14", 128], ["3/2", 32], ["3/5", 8], [4])
_test.pt()
print("\n减多项二次根式测试:")
print('>>>_test.sub(PR(["3/2",162], ["3/4",27])).pt()')
_test.sub(PR(["3/2",162], ["3/4",27])).pt()
print("\n加多项二次根式测试:")
print('>>>_test.add(["2.5", 125], PR(["7.5", 45])).pt()')
_test.add(["2.5", 125], PR(["7.5", 45])).pt()
print("\n乘多项二次根式测试:")
print('>>>_test.mul([1,2],[3, 5]).pt()')
_test.mul([1,2],[3, 5]).pt()
print("\n多项二次根式除以常数测试:")
print('>>>_test.div("-1/2").pt() ')
_test.div("-1/2").pt()
print("\n多项二次根式乘方测试:")
print('>>>PR([1,2],[1,3]).pow(5).pt()')
PR([1,2],[1,3]).pow(5).pt()
print("\n多项二次根式除以一项二次根式测试:")
print('>>>_test.div(["-1/2", 8]).pt() ')
_test.div(["-1/2", 8]).pt()
print("\n多项二次根式除以二项二次根式测试:")
print('>>>_test.div(["-1/2", 8],[1]).pt() ')
_test.div(["-1/2", 8],[1]).pt()
附录4:
#开方符合书写,只能从左到右书写
def writeSqrt(aTurtle, base, index=2, pensize=2, font=("Arial",17,"normal")):
'''
@aTurtle 一个海龟
@base 底数
@index 指数
@pensize 画根号的笔大小
@font 字体
'''
#保持海龟原来的参数后设置参数
speed = aTurtle.speed()
aTurtle.speed(0)
isdown = aTurtle.isdown()
pos = aTurtle.pos()
old_pensize=aTurtle.pensize()
if isdown:
aTurtle.up()
#右移1字符写底数
aTurtle.setx(pos[0]+font[1])
aTurtle.write(base, move=True, font=font)
pos2=aTurtle.pos()
#写指数
if index != 2:
aTurtle.setpos(pos[0]+font[1]*0.75,pos[1]+font[1]*0.5)
aTurtle.write(index, align="right", font=("Arial",font[1]//2,"normal"))
#原位右移1/4格画根号
aTurtle.pensize(pensize)
aTurtle.setpos(pos[0]+font[1]*0.25,pos[1]+font[1]*0.25)
aTurtle.down()
aTurtle.setpos(pos[0]+font[1]*0.5,pos[1]+font[1]*0.5)
aTurtle.setpos(pos[0]+font[1]*0.75,pos[1]+font[1]*0.25)
aTurtle.setpos(pos[0]+font[1],pos[1]+font[1]*1.4)
aTurtle.setpos(pos2[0],pos2[1]+font[1]*1.4)
aTurtle.up()
#恢复
aTurtle.speed(speed)
aTurtle.setpos(pos2)
aTurtle.pensize(old_pensize)
if isdown:
aTurtle.down()
if __name__ == "__main__":
import turtle as t
t.setup(200,200)
t.screensize(180,180)
t.shape("turtle")
t.up()
writeSqrt(t,3)
t.sety(50)
writeSqrt(t,-56,-3,font=("Arial",20,"normal"))
t.ht()
t.mainloop()