这里讨论的都是可以用函数解析法表示的函数。我们现在从最简单的函数：

y=x

开始研究函数。首先我们来看这个函数的图象：

可见，它是过原点的平分第一和第三象限的直线。如果用-x代替x，即：

y=-x

函数的图象：

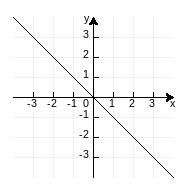
可见，它是过原点的平分第二和第四象限的直线。

　　用３x，-3x，x/3和-x/3代替x，即：

y=3x、

y=-3x、

y=x/3、

y=-x/3。

为了更好说明问题，把它们和y=x、y=-x画在一起（作图代码附录１）：

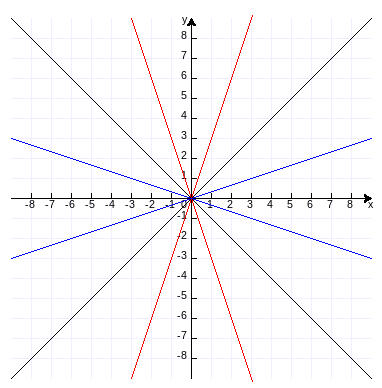
注：y=x、y=-x为黑色；y=3x、y=-3x为红色；y=x/3、y=-x/3为蓝色。　

　　上面这些函数都是常数与自变量的积的形式。一般地，形如y=kx（k是常数，k≠0）的函数，叫做正比例函数(proportional function)，其中k叫做比例系数。由上图可得正比例函数图象（直线）的特性：

（１）都过原点。

（２）当k>0，在第一和第三象限，y随x增大而增大；当k<0时在第二和第四象限，y随x增大而减少。

（３）当k的绝对值大于１时，函数图象（直线）更靠近y轴；当k的绝对值小于１时，函数图象（直线）更靠近x轴。

　　如果用一个一元一次多项式（±x±2）代替y=x（黑色线）中的自变量x，即y=x＋2和y=-x+2（红色线）、y=x-2和-x-2（蓝线），增加y=－x（黑色线）（作图代码附录2）：

可见，y=x+2和y=-x+2的直线分别是y=x和y=-x的直线向上平移2个单位，y=x-2和y=-x-2的直线分别是y=x和y=-x的直线向下平移2个单位。

　　在正比例函数y=kx中增加１个常数项b就成了（一元）一次函数y=kx+b，当b>0时，图象直线向上平移b个单位；当b<0时，图象直线向下平移|b|个单位；当b=0时是正比例函数本身。

　　一元一次函数y=kx+b(k≠0,b≠0)的图象直线的特点列举如下：

（１）过纵坐标轴上点(0, b)。

（２）当k>0，过第一和第三象限，y随x增大而增大，b>0过第二象限，b<0过第四象限；当k<0时在第二和第四象限，y随x增大而减少，b>0过第一象限，b<0过第三象限。

（３）当k的绝对值大于１时，函数图象（直线）更靠近y轴；当k的绝对值小于１时，函数图象（直线）更靠近x轴。

　　例题1：通过函数轨迹模块作y=4x-2与y=-0.25x+3的图象，观察两条直线的关系，提出你的猜想，然后证明你的猜想。

解：作图（代码附录3）

可见，两条直线互相垂直。由于常数线是直线的平移，因此这两条直线相应的正比例直线也是相互垂直的。看它们的

比例系数乘积＝4×(-0.25)＝-1，

从而得到猜想：比例系数乘积等于-1的两条一次函数直线相互垂直。

画直线y=ax、y=-(1/a)x（a≠0）和y=b（b≠0三条直线（作图代码附录4）：

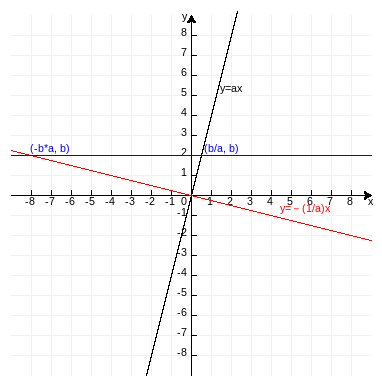
证明：

围成的三角形两边平方和

＝(-b*a)²＋b²+(b/a)²+b²

＝b²(a²+2+(1/a)²)

=(b*a+b/a)²

＝第三边平方。

所以这两条直线垂直。

　　例题2：已知坐标平面上两点(2, 5)、(-4, -9)，求这两点的对称轴直线的函数解析式。

解：由于一次函数的直线都可以由正比例函数平移所得，平移过程比例系数不变，设想把坐标系平移到(-4,-9)点，那另外一个点就是(6,14)，因此，该直线与过(0,0)、(6,14)直线的比例系数相同：

k=14/6=7/3。

那对称轴的比例系数：

k'=-1/k=-3/7。

对称轴过两点连线的中点：x=(2-4)/2=-1，y=(5-9)/2=-2，即(-1, -2)点。

设对称轴的解析式是：y=-3/7x+b，则：

-2=3/7+b

b=-17/7。

即　y=-3/7x-17/7。

作图验证（代码附录5）：

　　例题3：已知函数y=4x-3，求过点(-1,1)并且与这个函数的图象直线平行的直线函数解析式。

解：由于与y=4x-3平行，设要求的函数是y=4x+b，则：

1=4×(-1)+b，

b=5，

得函数解析式为：y=4x+5。

作图验证y=4x-3（黑色），y=4x+5（蓝色）（作图代码附录6）：

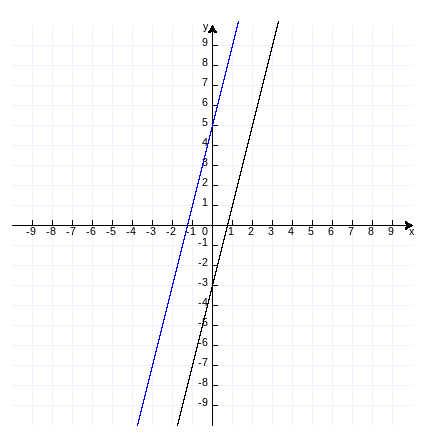
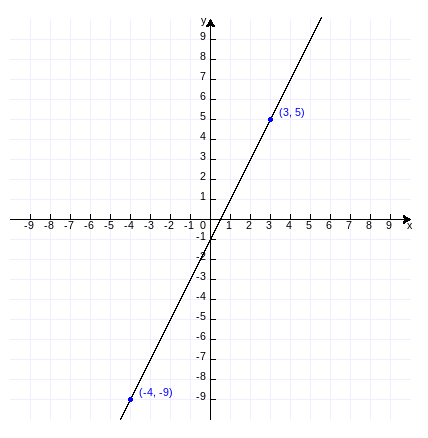
例题4：已知一次函数的图象过点(3,5)与(-4,-9)，求这个一次函数的解析式。

解：设想把坐标系移到(-4,-9)点，那另一点坐标是(7,14)，设这时的解析式是

y=kx，

则

14=k×7，

k=2。

再设要求的解析式是

y=2x+b

则

5=2×3+b，

b=-1。

得要求解析式

y=2x-1。

作图验证（作图代码附录7）：

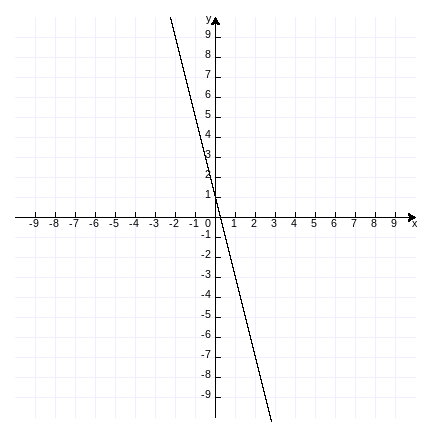
例题5：已知常数a≠0，b≠0，直线y=-a²x+b²与x轴交点坐标为______，与y轴交点坐标为________，图象经过________________象限，y随x的增大而______。

解：x轴交点，这时y=0，由0=-a²x+b²得x=b²/a²，即与x轴交点坐标为(b²/a²,0)；同理的与y轴交点坐标为(0, b²)；由于-a²<0，直线必过第二和第四象限，又由于b²>0，直线是正比例直线向上平移的，所以必过第一象限，即图象经过第一、第二、第四象限；由于-a²<0，y随x的增大而减少。

令a=2，b=1，即函数y=-4x+1，作图验证（作图代码附录8）：

例题6：“益田”牌小麦种子的价格为12元/kg，如果一次购买超过200kg，超过的部分的种子价格打8折。

（1）填写下面表格：

（2）写出付款金额关于购买量的函数解析式，并画出函数图象。

　　分析：付款金额与种子价格相关，问题中种子价格不是固定不变的，它与购买量有关。设购买xkg种子，当0≤x≤200时，种子价格为12元/kg；当x>200时，其中有200kg种子按12元/kg计价，其余的(x-200)kg(即超出200kg部分)种子按9.6元/kg（即8折)）计价。因此，写函数解析式与画函数图象时，应对0≤x≤200和x>200分段讨论。

解：（1）

(2)设购买量为x kg，付款金额为y元。

当0≤x≤200时，y=12x；

当x>200时，y=9.6(x-200)+12*200=9.6x+480。

函数图象如图下图（作图代码附录9）：

　　我们表示一次函数用一条直线，但如果是线段或射线，如上例，就要加入自变量的取值范围0≤x≤200和x>200，这样把自变量的取值范围称作函数的定义域，相对于定义域的函数值范围就称作值域。上例中，与定义域0≤x≤200相对的值域是0≤y≤2400；与定义域x>200相对的值域是y>2400。

练习题：

1、已知常数a≠0，b≠0，直线y=2a²x-3b²与x轴交点坐标为______，与y轴交点坐标为________，图象经过________________象限，y随x的增大而______。

2、已知一次函数的图象过点(3,2)、(-4,a)与(a,-4)，求这个一次函数的解析式。

3、已知函数y=-3x-2，求过点(2,3)并且与这个函数的图象直线平行的直线函数解析式。

4、已知坐标平面上两点(-3, -4)、(3, 14)，求这两点的对称轴直线的函数解析式。

５、汽车从A出发，速度50km/h，3小时后提高速度50%。

（1）填写下面表格：

（2）写出路程关于时间的函数解析式，并画出函数图象。

（3）指出定义域和值域。

附录１：

import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(400,400)
t.screensize(360,360)

build(t)
a=1
def f(x):
    return a*x
 
#y=x   
trace(t,-9,9,f)
#y=-x   
a=-1
trace(t,-9,9,f)
t.pencolor("red")
#y=3x
a=3
trace(t,-9,9,f)
#y=-3x
a=-3
trace(t,-9,9,f)
t.pencolor("blue")
#y=x/3
a=Fraction(1,3)
trace(t,-9,9,f)
#y=-x/3
a=-Fraction(1,3)
trace(t,-9,9,f)
t.ht()

附录2：

import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(400,400)
t.screensize(360,360)

build(t)
a=1
b=0
def f(x):
    return a*x+b
 
#y=x   
trace(t,-9,9,f)
#y=-x
a=-1
trace(t,-9,9,f)
t.pencolor("red")
#y=x+2  
a=1
b=2
trace(t,-9,9,f)
#y=-x+2  
a=-1
trace(t,-9,9,f)
t.pencolor("blue")
#y=x-2   
a=1
b=-2
trace(t,-9,9,f)
#y=-x-2   
a=-1
trace(t,-9,9,f)
t.ht()

附录3：

import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(400,400)
t.screensize(360,360)
t.up()
build(t)
a=4
b=-2
def f(x):
    return a*x+b
 
#y=4x-2   
trace(t,-9,9,f)
t.setpos(2.5*20,6*20)
t.write("y=4x-2")
t.pencolor("red")
#y=－0.25x+3
a=-Fraction(1,4)
b=3
trace(t,-9,9,f)
t.setpos(4.5*20,2*20)
t.write("y=－0.25x+3")
t.ht()

附录4：

import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(400,400)
t.screensize(360,360)
t.up()
build(t)
a=4
b=0
def f(x):
    return a*x+b
 
#y=4x  
trace(t,-9,9,f)
t.setpos(1.5*20,5*20)
t.write("y=ax")
t.pencolor("red")
#y=－0.25x
a=-Fraction(1,4)
trace(t,-9,9,f)
t.setpos(4.5*20,-20)
t.write("y=－(1/a)x")
t.setpos(-9*20,2*20)
t.down()
t.pencolor("blue")
t.setx(9*20)
t.up()
t.setpos(14,2*20)
t.write("(b/a, b)")
t.setpos(-8*20,2*20)
t.write("(-b*a, b)")
t.ht()

附录5：

import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t)
#
t.setpos(-4*20,-9*20)
t.dot("blue")
t.down()
t.setpos(2*20,5*20)
t.dot("blue")
t.up()
def f(x):
    return -Fraction(3,7)*x-Fraction(17,7)
 
t.pencolor("red")
trace(t,-10,10,f)
t.ht()

附录6：

import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t)
a=4
b=-3
def f(x):
    return a*x+b
#y=4x-3
trace(t,-10,10,f)
t.pencolor("blue")
b=5
trace(t,-10,10,f)
t.ht()

附录7：

import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t)
a=2
b=-1
def f(x):
    return a*x+b
#y=2x-1
trace(t,-10,10,f)
#端点
t.pencolor("blue")
t.setpos(3*20,5*20)
t.dot("blue")
t.setx(3*20+10)
t.write("(3, 5)")
t.setpos(-4*20,-9*20)
t.dot("blue")
t.setx(-4*20+10)
t.write("(-4, -9)")
t.ht()

附录8：

import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t)
a=-4
b=1
def f(x):
    return a*x+b
#y=-4x+1
trace(t,-10,10,f)
t.ht()

附录9：

import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(600,600)
t.screensize(500,500)
t.up()
build(t, xUnt = (50,40), yUnt = (500,40), wc = (-50,-50,450,450))
a=12
b=0
def f(x):
    return a*x+b
#y=12x
t.pencolor("red")
trace(t,0,200,f)
t.setpos(40,80)
t.write("y=12x")
#y=9.6x+480
t.pencolor("blue")
a=9.6
b=480
trace(t,200,4500,f)
t.setpos(240,250)
t.write("y=9.6x+480")
t.ht()

​