在函数y=ax+b中如果a=0,不难想象,它是过(0,b)点,平行与x轴的一条直线。用函数轨迹验证一下(作图代码附录1):

也就是说,y=b是一条平行于x轴的直线。我们知道,不平行的两条直线相交于一点。在上图中再画一条直线y=ax+c(a≠0),增加的代码见附录2:
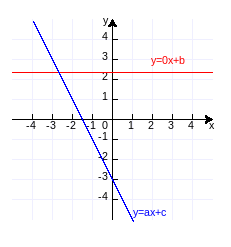
交点的纵坐标是b,横坐标是函数y=ax+c的函数值是b时的x值,也就是方程:
ax+c=b
的解。到此,我们才领悟到,方程是知道函数值,反推自变量的值;实质是一条直线与平行于x轴的直线交点。
例题1:方程-123456789x-987654321=111111111的解大于0还是小于0?
解:函数y=-123456789x-987654321的比例系数<0,对应的正比例函数y=-123456789x经过第二和第四象限,-987654321<0,正比例函数线向下平移,这样经过第三象限;而y=111111111是一条经过第一和第二象限的的直线,与y=-123456789x-987654321的交点必在第二象限,所以方程-123456789x-987654321=111111111的解小于0。
解方程时,要联想到相应的函数的直线,这样会减少犯错的几率。
例题2:方程-12345x+54321=168x的解大于0还是小于0?
解:函数y=-12345x+54321经过第一、第二和第四象限;函数y=168x经过第一和第三象限,这两个函数必相交与第一象限,所以解大于0。
当方程等号两边都有未知数时,就要考虑一般直线相交的情况。
我们可以直接看出像4x=24、x+1=3这样的简单方程的解,但是仅靠观察来解比较复杂的方程是困难的。因此,我们还要讨论怎样解方程。方程是含有未知数的等式,为了讨论解方程,我们先来看看等式的性质:
等式的性质1 等式两边加(或减)同一个数(或式子),结果仍相等。
如果a=b,那么a±c=b±c。
等式的性质2 等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
如果a=b,那么ac=bc;
如果a=b(c≠0),那么a/c=b/c。
等式的性质3 等式任何的量用它的等量代替,结果仍相等。
例如:a+b=c,b=d-e,
那么a+d-e=c。
解一元一次方法步骤:
第一步:去分母(等式的性质2);
第二步:去括号(乘法分配绿);
第三步:移项(等式的性质1);
第四步:合并同类项(乘法分配率);
第五步:系数化为1(等式的性质2)。
例题3:解下列方程:

由上例可见,解一元一次方程是比较“机械”的,可以用Python编写一个程序来解决,结果输出如下(代码附录3):
Python执行信息开始:
原式=3/4x-3
方程解:x=4。
原式=25/6x-23/6
方程解:x=23/25。
Python执行信息结束。
练习题:解下面方程,懂Python的用上例方法进行验证:

附录1:
import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(200,200)
t.up()
build(t)
a=0
b=Fraction(7,3)
def f(x):
return a*x+b
#y=0x+b
t.pencolor("red")
trace(t,-10,10,f)
t.setpos(40,20*b+5)
t.write("y=0x+b")
t.ht()
附录2:
#y=ax+c
t.pencolor("blue")
a=-2
b=-3
trace(t,-10,10,f)
t.setpos(22,-20*5)
t.write("y=ax+c")
附录3:
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.zhengshiyunsuan import * #附录4
#化为标准一元一次方程ax+b=0后解
def oneFun(l,r):
f=l.sub(r)
f.pt()
if len(f.terms)==0:
print("这是个恒等式。")
elif len(f.terms)==1:
t=f.terms[0]
if t.powers==None:
if t.coefficient==None or t.coefficient==0:
print("这是个恒等式。")
else:
print("方程无解。")
else:
if t.coefficient==None or t.coefficient==0:
print("这是个恒等式。")
else:
print("方程解:%s=0。" % t.powers[0].baseNumber)
else:
t1=f.terms[0]
t2=f.terms[1]
print("方程解:%s=%s。" % (t1.powers[0].baseNumber, Fraction(-t2.coefficient,t1.coefficient)))
#1、(x+1)/2-1=2+(2-x)/4
left=Pn([1,(x)],[1]).div(2).add([-1])
right=Pn([2]).add(Pn([2],[-1,(x)]).div(4))
oneFun(left, right)
#2、3x+(x-1)/2=3-(2x-1)/3
left=Pn([3,(x)]).add(Pn([1,(x)],[-1]).div(2))
right=Pn([3]).sub(Pn([2,(x)],[-1]).div(3))
oneFun(left, right)
附录4:
'''整式加、减、乘、乘方和除以非零有理数运算
@作者 码老师
@微信公众号 学思营 ID:xuesying
@公司 深圳五行星软件有限公司
@日期 2020-10-29
@使用方法
1、导入模块
>>>from zhengshiyunsuan import *
2、单项式
整数单项式例如:
>>>Mn(3)
分数单项式例1:
>>>Mn("1/2")
分数单项式例2:
>>>from fractions import Fraction
>>>Mn(Fraction(1, 2))
小数单项式(字符串输入,系统自动转为分数):
>>>Mn("3.14")
如果单项式有代数,字母和指数作为元组列举在常数之后,例如
>>>Mn("3.14", (x, 2), (y, 2))
注意:指数一定是正整数,如果是1次方,可以省略,例如
>>>Mn("3.14", (x), (y))
3、多项式
空多项式:
>>>pn = Pn()
>>>pn.pt()
可以有列表化单项式,单项式和多项式参数,例如:
>>>m1 = Mn("3.14", (x, 2), (y, 2))
>>>p1 = Pn([12, (x, 3), (y, 3)])
>>>_test = Pn(m1, p1, Mn("2/3", (z)), Pn(m1, [9, (y, 2), (z, 2)]), ["5/3", (z)])
>>>_test.pt()
4、加多项式:
>>>_test.add(["2.5", (x,3)], Pn(["7.5", (x,3)])).pt()
5、减多项式:
'>>>_test.sub(Pn(["3/2",(z),(x)], ["3/4",(x),(z)])).pt()
6、乘多项式:
>>>_test.mul([1,(x)],[1]).pt()
7、除以常数:
>>>_test.div("-1/2").pt()
8、乘方:")
>>>Pn([1,(x)],[1,(y)]).pow(5).pt()
'''
from fractions import Fraction
class _Power:
'''乘方和幂'''
#底数,单字母
baseNumber = None
#指数,正整数
exponent = 1
#克隆
def clone(self):
return _Power(self.baseNumber, self.exponent)
#字母比较
def cmp(power, otherPower, isDifferent=True):
a = power.baseNumber
b = otherPower.baseNumber
if a > b:
return 1
elif a < b:
return -1
else:
if isDifferent:
return otherPower.exponent-power.exponent #字母相同,指数大的排前
else:
return 0 #用于同一个单项式里合并同字母幂
#打印
def __str__(self):
if self.baseNumber == None:
return ""
else:
if self.exponent > 1:
return "(%s%d)" % (self.baseNumber, self.exponent)
else:
return self.baseNumber
#构造方法
def __init__(self, baseNumber, exponent=1):
if baseNumber == None or exponent == None:
raise ValueError("底数和指数不能为空!")
if not isinstance(exponent, (int)) or exponent < 1:
raise ValueError("指数只能是正整数!")
self.baseNumber = baseNumber
self.exponent = exponent
class Mn:
'''单项式Monomial'''
#系数,非零有理数(分数)
coefficient = None
#代数,Power的列表
powers = None
#相反数
def opp(self):
if self.coefficient != None:
self.coefficient = -self.coefficient
return self
#克隆
def clone(self):
m = Mn(self.coefficient)
if self.powers != None and len(self.powers) > 0:
m.powers = []
for power in self.powers:
m.powers.append(power.clone())
return m
#单项式次数
def degreeOfAMonomial(self):
t = 0
if self.powers != None and len(self.powers) > 0:
for power in self.powers:
t += power.exponent
return t
#比较大小:幂阶降序,字母升序。
#第二个要在前正值;合并0;其它负值
def cmp(monomial, otherMonomial):
d1 = monomial.degreeOfAMonomial()
d2 = otherMonomial.degreeOfAMonomial()
if d1 != d2:
return d2 - d1 #如果d2>d1 d2-d1>0要把第二个插入第一个的位置
else:
if d1 == 0:
return 0 #两个都是常数项
len1= len(monomial.powers) #第一个元数
len2= len(otherMonomial.powers) #第二个元数
maxLen = max(len1, len2)
for i in range(maxLen):
t = monomial.powers[i].cmp(otherMonomial.powers[i])
if t != 0:
return t #第二个在后的话t>0,需要插入
if len1 != len2:
return len2 - len1 #如果len2>len1,则len2-len1>0,则第二个要插入第一个的位置
return 0 #同类项
#按底的字母顺序排序,同底指数合并
def _sort1(powers, idx, num):
power = powers[num]
for i in range(idx+1):
m = powers[i]
t = m.cmp(power, False)
if t == 0: #合并同类项
m.exponent += power.exponent
return idx
elif t >0: #新的高阶项,高阶项插入当前位置
idx += 1
for p in range(idx, i, -1): #后推其它项
powers[p] = powers[p-1]
powers[i] = power #插入该项
return idx #返回结果数
idx += 1
powers[idx] = power #把新项插在结果最后
return idx
def _sort(powers):
idx = 0 #结果下标
lth = len(powers)
for num in range(1, lth):
idx = Mn._sort1(powers, idx, num) #排序和合并1项
idx += 1
if idx < lth:
del(powers[idx:])
for power in powers:
if power.exponent == 0: #去除字母是0的元
del(power)
return powers;
#单项式相乘
def mul(first, second):
first.coefficient *= second.coefficient
if first.powers == None or len(first.powers) == 0:
first.powers = second.powers
elif second.powers != None and len(second.powers) >0:
first.powers.extend(second.powers)
first.powers = Mn._sort(first.powers)
return first
#打印
def print(self, isFirst):
if self.coefficient == None or self.coefficient == 0:
return ""
else:
if self.coefficient == 1:
s = ""
elif self.coefficient == -1:
s = "-"
else:
s = str(self.coefficient)
if self.coefficient > 0:
if not isFirst:
s = "+" + s
if self.powers != None and len(self.powers) > 0: #非常数项
for power in self.powers:
s += str(power)
return s
#打印
def __str__(self):
return self.print(False)
#构造方法
def __init__(self, coefficient, *powers):
if coefficient == None: #空单项式,与0相同
return
if not isinstance(coefficient, (int, Fraction, str)):
raise ValueError("单项式系数只能是整数、分数(Fraction)或字符串(小数和分数)")
self.coefficient = Fraction(coefficient)
if self.coefficient != 0:
if powers != None and len(powers) > 0:
prs = []
for power in powers:
prs.append(_Power(*power)) #参数解包
self.powers = Mn._sort(prs)
class Pn:
'''多项式Polynomial'''
#项Monomial列表
terms = None
#克隆
def _clone(self):
p = Pn()
if self.terms == None or len(self.terms) == 0:
return p
lth = len(self.terms)
t = []
for i in range(lth):
t.append(self.terms[i].clone())
p.terms = t
return p
#合并同类项与排序
def _sort1(terms, idx, num):
term = terms[num] #需检查的元素
for i in range(idx+1): #把元素插入或合并到结果中
m = terms[i]
t = m.cmp(term) #比较
if t == 0: #合并同类项
m.coefficient += term.coefficient
return idx
elif t > 0: #新的高阶项,高阶项插入当前位置
idx += 1
for p in range(idx, i, -1): #后推其它项
terms[p] = terms[p-1]
terms[i] = term #插入该项
return idx #返回结果数
idx += 1
terms[idx] = term #把新项插在结果最后
return idx
#合并同类项与排序
def _sort(terms):
idx = 0 #结果下标
lth = len(terms)
for num in range(1, lth):
idx = Pn._sort1(terms, idx, num) #排序和合并1项
#print("idx=%d" % idx)
#消除0系数项
temp = []
for num in range(idx +1):
term = terms[num]
if term.coefficient != 0:
temp.append(term)
nlth = len(temp)
if nlth == 0:
del(terms[0:])
return terms
else:
for num in range(nlth):
terms[num] = temp[num]
if nlth < lth:
del(terms[nlth:])
return terms;
#加
def _add(self, isSub, *terms):
if terms != None and len(terms) > 0:
if self.terms == None:
self.terms = []
for term in terms:
if isinstance(term, Pn):
if term.terms != None and len(term.terms) > 0:
for t in term.terms:
if isSub:
self.terms.append(t.clone().opp()) #克隆,保证原式不受影响
else:
self.terms.append(t.clone())
else:
if isinstance(term, Mn):
if isSub:
self.terms.append(term.clone().opp()) #克隆防止影响原对象
else:
self.terms.append(term.clone())
else:
if isSub:
self.terms.append(Mn(*term).opp()) #解包list添加1个单项式,无需克隆
else:
self.terms.append(Mn(*term))
Pn._sort(self.terms) #排序
def add(self, *terms):
s = self._clone() #克隆防止改变原对象
s._add(False, *terms)
return s
#减
def sub(self, *terms):
s = self._clone() #克隆防止改变原对象
s._add(True, *terms)
return s
#乘除常数,私有方法不克隆
def _muldiv(self, fraction, isdiv):
if self.terms != None and len(self.terms) >0:
try:
p = Fraction(fraction)
for term in self.terms:
if isdiv:
term.coefficient /= p
else:
term.coefficient *= p
except Exception as e:
print(e)
return self
#多项式乘单项式,私有方法都不可以克隆
def _mul(pn, mn):
for term in pn.terms:
term.mul(mn)
return pn
#乘
def mul(self, *terms):
if terms == None or len(terms) == 0: #空调用返回自己
return self
if len(terms) == 1 and isinstance(terms[0],(int, str)): #乘一个有理数
return self._clone()._muldiv(terms[0], False) #需要克隆对象
p = Pn(*terms) #建立要乘的多项式 如果里面有Mn或Pn,则它们会被克隆
if self.terms == None or len(self.terms) == 0: #self是空多项式可忽略
return p
elif p.terms != None and len(p.terms) >0:
lth = len(p.terms)
s = self._clone()._mul(p.terms[0]) #乘单项式
if lth == 1:
return s
for i in range(lth-1): #克隆对象乘
s._add(False, self._clone()._mul(p.terms[i+1]))
return s
else: #p为空多项式
return self;
#乘方
def pow(self, num):
if not isinstance(num, (int)) or num < 2:
print("请输入大于1的整数")
return self
if self.terms == None or len(self.terms) == 0:
return self
s = self._clone()
for i in range(num-1):
s = s.mul(self) # 由于mul会克隆,这里不用克隆
return s
#除
def div(self, fraction):
return self._clone()._muldiv(fraction, True)
#print用
def __str__(self):
s = "原式="
if self.terms == None or len(self.terms) == 0:
s += "0"
else:
s += self.terms[0].print(True)
for i in range(1, len(self.terms)):
s += self.terms[i].print(False)
return s
#打印出多项式
def pt(self):
print(self)
#构造方法
def __init__(self, *terms):
self._add(False, *terms)
#定义字母
A = "A"
B = "B"
C = "C"
D = "D"
E = "E"
F = "F"
G = "G"
H = "H"
I = "I"
J = "J"
K = "K"
L = "L"
M = "M"
N = "N"
O = "O"
P = "P"
Q = "Q"
R = "R"
S = "S"
T = "T"
U = "U"
V = "V"
W = "W"
X = "X"
Y = "Y"
Z = "Z"
a = "a"
b = "b"
c = "c"
d = "d"
e = "e"
f = "f"
g = "g"
h = "h"
i = "i"
j = "j"
k = "k"
l = "l"
m = "m"
n = "n"
o = "o"
p = "p"
q = "q"
r = "r"
s = "s"
t = "t"
u = "u"
v = "v"
w = "w"
x = "x"
y = "y"
z = "z"
if __name__ == "__main__":
print("\n多项式测试:")
print("\n导入整式运行模块:")
print('>>>from zhengshiyunsuan import *')
print("\n构造函数测试:")
print('>>>_mn = Mn("3/2", (x, 2))')
print('>>>_pn = Pn(["3/5", (z, 2)])')
print('>>>_test = Pn(["-3.14", (z, 2)], _mn, _pn, [4])')
print('>>>_test.pt()')
_mn = Mn("3/2", (x, 2))
_pn = Pn(["3/5", (z, 2)])
_test = Pn(["-3.14", (z, 2)], _mn, _pn, [4])
_test.pt()
print("对比")
print('>>>_test = Pn(["-3.14", (z, 2)], ["3/2", (x, 2)], ["3/5", (z, 2)], [4])')
print('>>>_test.pt()')
_test = Pn(["-3.14", (z, 2)], ["3/2", (x, 2)], ["3/5", (z, 2)], [4])
_test.pt()
print("\n减多项式测试:")
print('>>>_test.sub(Pn(["3/2",(z),(x)], ["3/4",(x),(z)])).pt()')
_test.sub(Pn(["3/2",(z),(x)], ["3/4",(x),(z)])).pt()
print("\n加多项式测试:")
print('>>>_test.add(["2.5", (x,3)], Pn(["7.5", (x,3)])).pt()')
_test.add(["2.5", (x,3)], Pn(["7.5", (x,3)])).pt()
print("\n乘多项式测试:")
print('>>>_test.mul([1,(x)],[1]).pt()')
_test.mul([1,(x)],[1]).pt()
print("\n多项式除常数测试:")
print('>>>_test.div("-1/2").pt() ')
_test.div("-1/2").pt()
print("\n多项式乘方测试:")
print('>>>Pn([1,(x)],[1,(y)]).pow(5).pt()')
Pn([1,(x)],[1,(y)]).pow(5).pt()
print("\n多项式乘方测试杨辉三角:")
print('>>>_t = Pn([1,(x)],[1,(y)])')
print('>>>for _i in range(11):')
print('... _t.pow(_i).pt()')
_t = Pn([1,(x)],[1,(y)])
for _i in range(11):
_t.pow(_i).pt()