在同一个坐标平面中作函数y=3x+4和y=3x-5的图象,作图代码附录1:
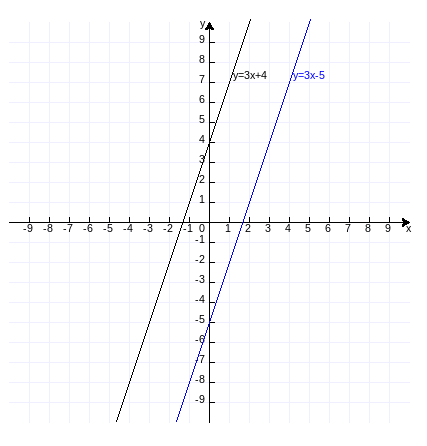
由于比例系数相同,所以两条直线是平行的。如果把这两个函数看做2条二元一次方程:
3x-y+4=0
3x-y-5=0
就构成了二元一次方程组。由于两条直线是平行,不存在点(x,y)使2个方程同时成立。
方程组中两方程的系数比相等,如果常数为0或比例也相等是同条方程,有无数个解,如果常数不为0或比例不相等无解;两方程的系数比不相等,有唯一解。
例题1:判断下面方程组有唯一解、无解或无数解:
(1)
13x+4y+1=0,
39x+12y+5=0;
(2)
121x-11y+22=0,
11x-y+2=0;
(3)
3x+5y-10=0,
4x-7y+37=0。
解:(1) 13:39=4:12≠1:5,方程组无解;(2)121:11=-11:-1=22:2,方程组有无数解;(3) 3:4≠5:7,方程组有唯一解。
例题2:解下面方程组:
x-y=3 ①
3x-8y=14 ②
分析:我们已经会解一次方程,只要通过另一条方程使二元变一元,问题就可以解决了——这是转化思想:把复杂问题或不懂的问题化为已经解决的问题。二元一次方程组中有两个未知数,如果消去其中一个未知数,那么就把二元一次方程组转化为我们熟悉的一元一次方程。我们可以先求出一个未知数,然后再求另一个未知数。这种将未知数的个数由多化少、逐一解决的思想,叫做消元思想。
解:把①变换一下变为③:
x=y+3。 ③
把③代入②:
3(y+3)-8y=14。 ④
解这个方程,得:
y=-1。
把y=-1代入③,得:
x=2。
所以这个方程组的解是:
x=2,
y=-1。
上面的解法,是把二元一次方程组中一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法(substitution method)。
利用等式的性质3进行代入法解方程组,上例可以这样解:
把②变为:
3(x-y)-5y=14 ③
把①代入③,得:
9-5y=14 ④
解这个方程,得:
y=-1。
把y=-1代入①,得:
x=2。
所以这个方程组的解是:
x=2,
y=-1。
上面的解法说明,代入法不限于未知数,可以是式子,甚至已知数,只要达到消元就行。
例题3:解下面方程组:
5x=2y ①
500x+250y=22500000 ②
解:把500x拆分为100个5x,把①代入②,得:
200y+250y=22500000。 ③
解方程,得:
y=50000。
把y=50000代入①,得:
5x=2*50000。 ④
解得:
x=20000。
所以这个方程组的解是:
x=20000,
y=50000。
除了代入法,还有没有其他方法达到消元的目的呢?
例题4:解下面方程组:
x+y=10 ①
2x+y=16 ②
分析:两条方程比较接近,只要用等式性质1就可以把方程组解出来。
解:②-①(左边减左边,右边减右边)得
x=6
把x=6代入①,得
y=4。
所以这个方程组的解是
x=6,
y=4。
例题5:解下面方程组:
3x+10y=2.8 ①
15x-10y=8 ②
解:②+①(左边加左边,右边加右边)得
18x=10.8 ③
解得
x=0.6。
把x=0.6代入②,得
9-10y=8 ④
解方程,得
y=0.1。
所以这个方程组的解是
x=0.6,
y=0.1。
从上面两个方程组的解法可以看出:当二元一次方程组的两个方程中同未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程。这种方法叫做加减消元法,简称加减法(addition-subtraction method)。加减法的依据是等式的性质1。
如果未知数的系数都不相同,还能用加减法吗?
例题6:解下面方程组:
3x+4y=16 ①
5x-6y=33 ②
分析:这两个方程中没有同一个未知数的系数相反或相等,直接加减这两个方程不能消元。我们利用等式性质2对方程进行改造,使得这两个方程中某个未知数的系数相反或相等。
解:①×3(等号两边同时×3)得
9x+12y=48。 ③
②×2,得
10x-12y=66。 ④
③+④,得
19x=114,
x=6。
把x=6代入①,得
3×6+4y=16,
4y=-2,
y=-1/2。
所以这个方程组的解是
x=6,
y=-1/2。
代入消元法和加减消元法是二元一次方程组的两种解法,它们都是通过消元使方程组转化为一元一次方程,只是消元的
方法不同。我们应根据方程组的具体情况,选择适合它的解法。一般情况,能用加减法就用加减法;不能用加减法的考虑式子代入法;最后考虑未知数代入法。
例题7:解下面方程组:

(1)解:通过去括号和移项,把方程组改造为
3x-y=8, ①
3x-5y=-20。 ②
①-②,得
4y=28,
y=7。
把y=7代入①,得
3x-7=8。
解方程,得
x=5
所以这个方程组的解是
x=5,
y=7。
(2)解:第一条方程两边×12,第二条方程两边×30,去分母,得
8u+9v=6, ①
24u+25v=14。 ②
①×3-②,得
2v=4,
v=2。
把v=2代入①,得
8u+18=6,
u=-3/2。
所以这个方程组的解是
u=-3/2,
v=2。
从上一例题中可以看到,在用加减法解方程组之前,要通过去括号、去分母和移项把每个方程都化成ax+by=c的形式。
练习题1:判断下面方程组有唯一解、无解或无数解:
(1)
7x+4y+1=0,
49x+28y+7=0;
(2)
51x-12y+39=0,
17x-4y+12=0;
(3)
15x+4y-14=0,
4x-17y+23=0。
练习题2:

附录1:
import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t)
a=3
b=4
def f(x):
return a*x+b
#y=3x+4
trace(t,-10,10,f)
t.setpos(25, 140)
t.write("y=3x+4")
#y=3x-5
t.pencolor("blue")
b=-5
trace(t,-10,10,f)
t.setpos(85,140)
t.write("y=3x-5")
t.ht()