对于一元一次函数
y=3x+2,
已知函数值分别大于2(y>2)、小于0(y<0)、小于-1(y<-1),求自变量x的取值范围。或者说,在直线y=3x+2上取纵坐标分别满足大于2、小于0、小于-1的点,看它们的横坐标分别满足什么条件(下图)。

把y=3x+2分别代入y>2、y<0和y<-1得到三条式子
(1)3x+2>2,
(2)3x+2<0,
(3)3x+2<-1。
像上面(1)(2)(3),用符号“<”或“>”表示大小关系的式子,叫做不等式(inequality)。像a+2≠a-2、x+1≥3、x+1≤3这样用符号“≠(不等于)、≥(大于或等于)、≤(小于或等于)”表示不等关系的式子也是不等式。
有些不等式中不含未知数,例如3<4,-1>-2,这种不等式在程序中广泛使用,作为转折开关。有些不等式中含有未知数,例如(1)(2)(3)式中字母x表示未知数,这种不等式一般用于已知值域反推定义域——解不等式。
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集( solution set)。求不等式的解集的过程叫做解不等式。由图可得上面三条不等式的解集:
(1)x>0,
(2)x<-2/3,
(3)x<-1。
对于某些简单的不等式,我们可以直接得出它们的解集,例如不等式x+3>6的解集是x>3,不等式2x<8的解集是x<4。但是对于比较复杂的不等式,例如(5x+1)/6-2>(x-5)/4,直接得出解集就比较困难。因此,还要讨论怎样解不等式。与解方程需要依据等式的性质一样,解不等式需要依据不等式的性质。为此,我们先来看看不等式有什么性质。我们知道,等式两边加或减同一个数(或式子),乘或除以同一个数(除数不为0),结果仍相等。不等式是否也有类似的性质呢?
一般地,不等式有以下性质。
不等式的性质1 不等式两边加(或减)同一个(或相等)数(或式子)不等号的方向不变。
如果a>b,那么a±c>b±c。
不等式的性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变。
如果a>b,c>0,那么ac>bc(或a/c>b/c)。
不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变。
如果a>b,c<0,那么ac<bc(或a/c<b/c)。
不等式的性质4 两个同向不等式相加,不等号的方向不变。
如果a>b,c>d,那么a+c>b+d。
不等式的性质5 两个异向不等式相减,不等号的方向不变。
如果a>b,c<d,那么a-c>b-d。
不等式的性质6 两个量,一个大于某一个量而另一个小于某个量,那前一个量大于后一个量(不等关系的传递)。
如果a>b,b>c,那么a>c。
例题1:设m>n,用“<”或“>”填空:
(1)m-5_____n-5;
(2)m+4_____n+4;
(3)6m_____6n;
(4)-(1/3)m____-(1/3)n;
(5)若p>t,则m+p____n+t;
(6)若p<t,则m-p_____n-t;
(7)若n>p,则m____p。
解:
(1)m-5 > n-5;不等式的性质1
(2)m+4 > n+4; 不等式的性质1
(3)6m > 6n;不等式的性质2
(4)-(1/3)m < -(1/3)n; 不等式的性质3
(5)若p>t,则m+p > n+t;不等式的性质4
(6)若p<t,则m-p > n-t; 不等式的性质5
(7)若n>p,则m____p。不等式的性质6
例题2:解下列不等式,并在数轴上表示解集:
(1)x+3>-1;
(2)6x≤5x-7;
(3)-(1/3)x<2/3;
(4)4x≥-12。
解:
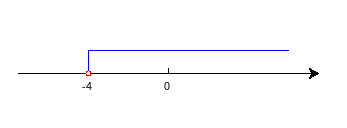
(1)x+3-3>-1-3,x>-4。数轴表示,作图代码附录1。
(2)6x-5x≤5x-7-5x,x≤-7。数轴表示,作图代码附录2。

(3)-(1/3)(-3)x>2/3(-3),x>-2。数轴表示,作图代码附录3。

(4)4x/4≥-12/4,x≥-3。数轴表示,作图代码附录4。
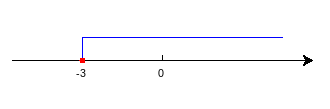
注意:≥、≤是实点,>、<是虚点。
练习1:设s>q,用“<”或“>”填空:
(1)s-123_____q-123;
(2)s+98_____q+98;
(3)13s_____13q;
(4)-(1/17)s____-(1/17)q;
(5)若p>t,则s+p____q+t;
(6)若p<t,则s-p_____q-t;
(7)若q>p,则s____p。
练习题2:解下列不等式,并在数轴上表示解集:
(1)2x+5≥-1;
(2)9x+8<5x;
(3)-(1/12)x<1/6;
(4)11x≥-121。
附录1:
import turtle as t
t.setup(400,400)
t.screensize(300,300)
t.up()
t.setpos(-150,0)
t.seth(0)
t.shape("classic")
t.down()
t.fd(300)
t.stamp()
t.up()
t.setx(0)
t.down()
t.seth(90)
t.fd(5)
t.up()
t.back(25)
t.write("0",align="center")
t.setpos(-80,0)
t.dot(6,"red")
t.dot(4,"white")
t.sety(-20)
t.write("-4",align="center")
t.fd(23)
t.down()
t.pencolor("blue")
t.fd(20)
t.seth(0)
t.fd(200)
t.ht()
附录2:
iimport turtle as t
t.setup(400,400)
t.screensize(300,300)
t.up()
t.setpos(-150,0)
t.seth(0)
t.shape("classic")
t.down()
t.fd(300)
t.stamp()
t.up()
t.setx(100)
t.down()
t.seth(90)
t.fd(5)
t.up()
t.back(25)
t.write("0",align="center")
t.setpos(10,0)
t.dot(6,"red")
t.sety(-20)
t.write("-7",align="center")
t.fd(23)
t.down()
t.pencolor("blue")
t.fd(20)
t.seth(180)
t.fd(140)
t.ht()
附录3:
import turtle as t
t.setup(400,400)
t.screensize(300,300)
t.up()
t.setpos(-150,0)
t.seth(0)
t.shape("classic")
t.down()
t.fd(300)
t.stamp()
t.up()
t.setx(0)
t.down()
t.seth(90)
t.fd(5)
t.up()
t.back(25)
t.write("0",align="center")
t.setpos(-80,0)
t.dot(6,"red")
t.dot(4,"white")
t.sety(-20)
t.write("-2",align="center")
t.fd(23)
t.down()
t.pencolor("blue")
t.fd(20)
t.seth(0)
t.fd(200)
t.ht()
附录4:
import turtle as t
t.setup(400,400)
t.screensize(300,300)
t.up()
t.setpos(-150,0)
t.seth(0)
t.shape("classic")
t.down()
t.fd(300)
t.stamp()
t.up()
t.setx(0)
t.down()
t.seth(90)
t.fd(5)
t.up()
t.back(25)
t.write("0",align="center")
t.setpos(-80,0)
t.dot(6,"red")
t.sety(-20)
t.write("-3",align="center")
t.fd(23)
t.down()
t.pencolor("blue")
t.fd(20)
t.seth(0)
t.fd(200)
t.ht()