如果一次不等式中有2个未知数,例如
y-x+5>0,
就是二元不等式了。与一元一次不等式相似,如何确定它的取值范围——解不等式呢?
我们把不等式转化为左边只有1个未知数(通常是y)而且系数为1,右边是另外一个未知数的多项式
y>x-5。
可以看到与函数
y=x-5
相近,事实上它们有不可分割的关系。当x取某个特定值p时,不等式就变成
y>p-5;
函数变成
y=p-5。
可见,当x取一个特点值p时,大于p-5的值都符合不等式的要求,在直角坐标系中是直线y=x-5的上方,所以这个二元一次不等式的解就是直线y=x-5的上方的区域。下面是示意图,作图代码附录1。

例题1:在直角坐标系纵画出下面二元一次不等式的示意图。
(1)4x+2y>5;
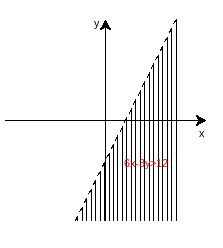
(2)6x-3y>12;
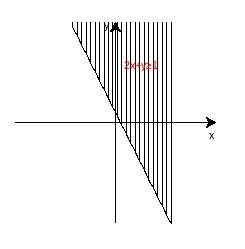
(3)2x+y≥1;
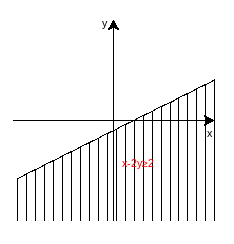
(4)x-2y≥2。
解:
(1)原式变为:y>-2x+5/2,作图代码附录2:
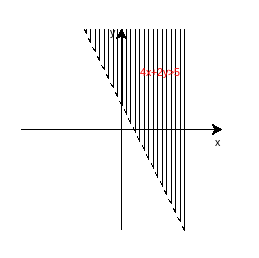
(2)原式变为:y<2x-4,作图代码附录3:
(3)原式变为:y≥-2x+1,作图代码附录4:
(4)原式变为:y≤1/2 x-1,作图代码附录5:
说明:>,<用虚线函数;≥,≤用实线函数。
练习题1:在直角坐标系中画出下面二元一次不等式的示意图。
(1)3x+2y>4;
(2)4x-3y>3;
(3)3x+y≥2;
(4)5x-2y≥4。
附录1:
import turtle as t
t.setup(300,300)
t.screensize(200,200)
t.up()
t.setpos(-100,0)
t.seth(0)
t.shape("classic")
t.down()
t.fd(200)
t.stamp()
t.up()
t.sety(-20)
t.write("x",align="right")
t.setpos(0,-100)
t.seth(90)
t.down()
t.fd(200)
t.stamp()
t.up()
t.setpos(-5,95)
t.write("y",align="right")
#画函数虚线
t.setpos(-50,-100)
t.seth(45)
d=0
isDown=True
while d<150*2**0.5:
if isDown:
isDown=False
t.down()
else:
isDown=True
t.up()
t.fd(5)
if d %10 ==0:
pos=t.pos()
if isDown:
t.down()
t.sety(100)
t.up()
t.setpos(pos)
if not isDown:
t.down()
d+=5
t.up()
t.setpos(20,50)
t.write("y>x-5")
t.ht()
附录2:
import turtle as t
import math
from fractions import Fraction
t.setup(300,300)
t.screensize(200,200)
t.up()
t.setpos(-100,0)
t.seth(0)
t.shape("classic")
t.down()
t.fd(200)
t.stamp()
t.up()
t.sety(-20)
t.write("x",align="right")
t.setpos(0,-100)
t.seth(90)
t.down()
t.fd(200)
t.stamp()
t.up()
t.setpos(-5,90)
t.write("y",align="right")
#画函数虚线
t.setpos(-10*(10-5/2)/2,100)
t.seth(math.atan(-2)*180/math.pi)
d=0
dx=5**0.5
dy=-dx*2
x,y =0, 100
isDown=True
while x<=100 and y>=-100:
if isDown:
isDown=False
t.down()
else:
isDown=True
t.up()
t.fd(5)
if d %10 ==0:
pos=t.pos()
if isDown:
t.down()
t.sety(100)
t.up()
t.setpos(pos)
if not isDown:
t.down()
d+=5
x+=dx
y+=dy
t.up()
t.setpos(20,50)
t.pencolor("red")
t.write("4x+2y>5")
t.ht()
附录3:
import turtle as t
import math
from fractions import Fraction
t.setup(300,300)
t.screensize(200,200)
t.up()
t.setpos(-100,0)
t.seth(0)
t.shape("classic")
t.down()
t.fd(200)
t.stamp()
t.up()
t.sety(-20)
t.write("x",align="right")
t.setpos(0,-100)
t.seth(90)
t.down()
t.fd(200)
t.stamp()
t.up()
t.setpos(-5,90)
t.write("y",align="right")
#画函数虚线
t.setpos(-30,-100)
t.seth(math.atan(2)*180/math.pi)
d=0
dx=5**0.5
dy=dx*2
x,y =-30, -100
isDown=True
while x<=100 and y<=100:
if isDown:
isDown=False
t.down()
else:
isDown=True
t.up()
t.fd(5)
if d %10 ==0:
pos=t.pos()
if isDown:
t.down()
t.sety(-100)
t.up()
t.setpos(pos)
if not isDown:
t.down()
d+=5
x+=dx
y+=dy
t.up()
t.setpos(20,-50)
t.pencolor("red")
t.write("6x-3y>12")
t.ht()
附录4:
import turtle as t
import math
from fractions import Fraction
t.setup(300,300)
t.screensize(200,200)
t.up()
t.setpos(-100,0)
t.seth(0)
t.shape("classic")
t.down()
t.fd(200)
t.stamp()
t.up()
t.sety(-20)
t.write("x",align="right")
t.setpos(0,-100)
t.seth(90)
t.down()
t.fd(200)
t.stamp()
t.up()
t.setpos(-5,90)
t.write("y",align="right")
#画函数虚线
t.setpos(-45,100)
t.seth(math.atan(-2)*180/math.pi)
d=0
dx=5**0.5
dy=-dx*2
x,y =-45, 100
while x<=100 and y>=-100:
t.fd(5)
if d %10 ==0:
pos=t.pos()
t.down()
t.sety(100)
t.up()
t.setpos(pos)
t.down()
d+=5
x+=dx
y+=dy
t.up()
t.setpos(10,50)
t.pencolor("red")
t.write("2x+y≥1")
t.ht()
附录5:
import turtle as t
import math
from fractions import Fraction
t.setup(300,300)
t.screensize(200,200)
t.up()
t.setpos(-100,0)
t.seth(0)
t.shape("classic")
t.down()
t.fd(200)
t.stamp()
t.up()
t.sety(-20)
t.write("x",align="right")
t.setpos(0,-100)
t.seth(90)
t.down()
t.fd(200)
t.stamp()
t.up()
t.setpos(-5,90)
t.write("y",align="right")
#画函数虚线
t.setpos(-100,-60)
t.seth(math.atan(1/2)*180/math.pi)
d=0
dy=5**0.5
dx=dy*2
x,y =-100, -60
while x<=100 and y<=100:
t.fd(5)
if d %10 ==0:
pos=t.pos()
t.down()
t.sety(-100)
t.up()
t.setpos(pos)
t.down()
d+=5
x+=dx
y+=dy
t.up()
t.setpos(10,-50)
t.pencolor("red")
t.write("x-2y≥2")
t.ht()