把一元一次绝对值的函数例如
y=2|x-1|-3
的等号改为不等号例如>就成了二元一次绝对值不等式
y>2|x-1|-3。
不难理解,这个不等式表示y=2|x-1|-3的上方,下图表示,作图代码附录1。
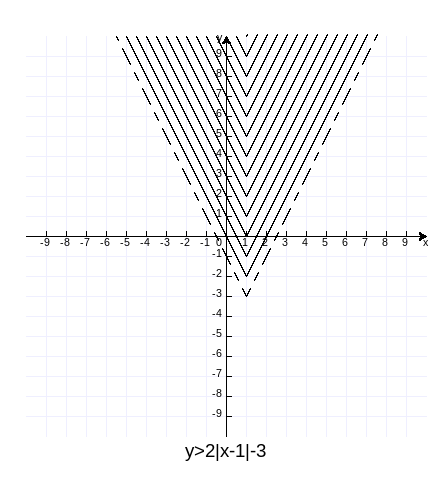
例题1:在直角坐标中标出
y<-2|x-2|+5
的解范围。
解:解范围如下图,作图代码附录2。
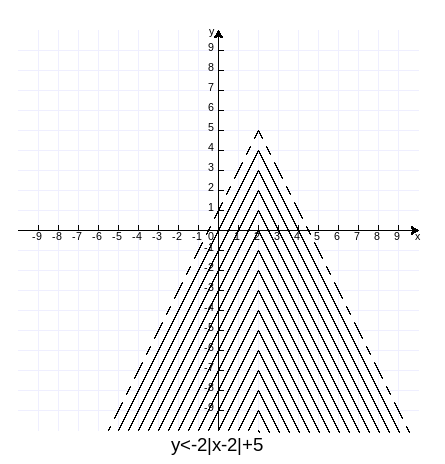
例题2:画出下面不等式组在直角坐标中的范围。
y<-2|x+1|+7, ①
y>3|x-1|-8。 ②
解:解范围如下图,作图代码附录3。
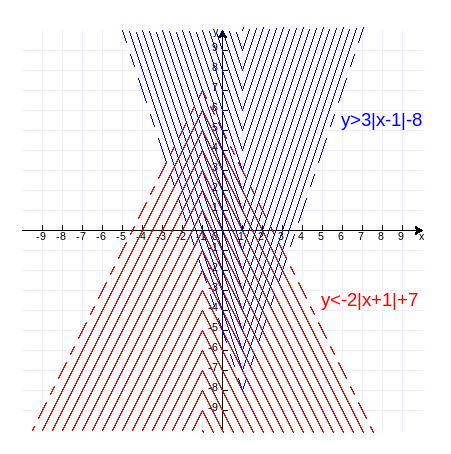
练习题1:画出下面不等式组在直角坐标中的范围。
y≤-3|x-1|+8, ①
y≥2|x+1|-7。 ②
附录1:
import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t)
#y=2|x-1|-3
a=2
b=-1
c=-3
def f(x):
temp=a*(x+b)
if temp>=0:
return temp+c
else:
return -temp+c
t.setpos(0, -225)
t.write("y>2|x-1|-3",align="center",font=(markFont[0],14,markFont[2]))
#画虚的函数线
for i in range(-10, 10):
trace(t,i,i+Fraction(1,5),f)
trace(t,i+Fraction(2,5),i+Fraction(3,5),f)
trace(t,i+Fraction(4,5),i+1,f)
#画实的函数线
while c<10:
c+=1
trace(t,-10,10,f)
t.ht()
附录2:
import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t)
#y=-2|x-2|+5
a=-2
b=-2
c=5
def f(x):
temp=a*(x+b)
if temp>0:
return -temp+c
else:
return temp+c
t.setpos(0, -225)
t.write("y<-2|x-2|+5",align="center",font=(markFont[0],14,markFont[2]))
#画虚的函数线
for i in range(-10, 10):
trace(t,i,i+Fraction(1,5),f)
trace(t,i+Fraction(2,5),i+Fraction(3,5),f)
trace(t,i+Fraction(4,5),i+1,f)
#画实的函数线
while c>-10:
c-=1
trace(t,-10,10,f)
t.ht()
附录3:
import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t)
t.pencolor("red")
#y<-2|x+1|+7
a=-2
b=1
c=7
def f(x):
temp=a*(x+b)
if temp>0:
return -temp+c
else:
return temp+c
t.setpos(100, -80)
t.write("y<-2|x+1|+7",font=(markFont[0],14,markFont[2]))
#画虚的函数线
for i in range(-10, 10):
trace(t,i,i+Fraction(1,5),f)
trace(t,i+Fraction(2,5),i+Fraction(3,5),f)
trace(t,i+Fraction(4,5),i+1,f)
#画实的函数线
while c>-10:
c-=1
trace(t,-10,10,f)
t.pencolor("blue")
#y>3|x-1|-8
a=3
b=-1
c=-8
def f2(x):
temp=a*(x+b)
if temp>0:
return temp+c
else:
return -temp+c
t.setpos(120, 100)
t.write("y>3|x-1|-8",font=(markFont[0],14,markFont[2]))
#画虚的函数线
for i in range(-10, 10):
trace(t,i,i+Fraction(1,5),f2)
trace(t,i+Fraction(2,5),i+Fraction(3,5),f2)
trace(t,i+Fraction(4,5),i+1,f2)
#画实的函数线
while c<10:
c+=1
trace(t,-10,10,f2)
t.ht()