在正比例函数

y=x

把x换成x²，就成了一元二次函数

y=x²。

也就是说，一个变量与另一个变量的平方成正比，这两个变量的关系就成了二次函数关系。现在假如用x轴的值表示x²，当x坐标小于0，与它对应的y坐标是它的相反数。图示如下，作图代码附录1。

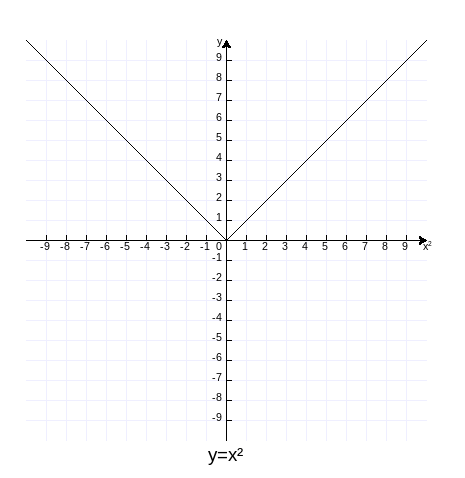
可见，二次函数与绝对值函数非常相似。把x轴换回真实的值，图象就是下面的样子了（作图代码附录2）

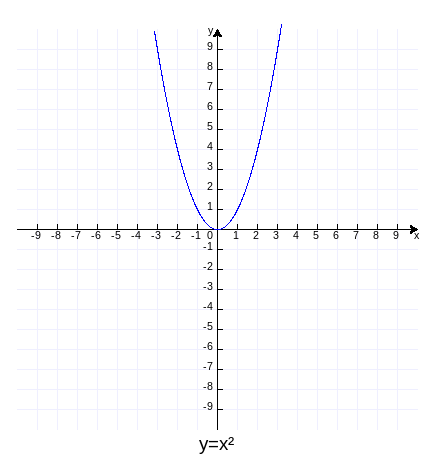
把这个图片倒过来看

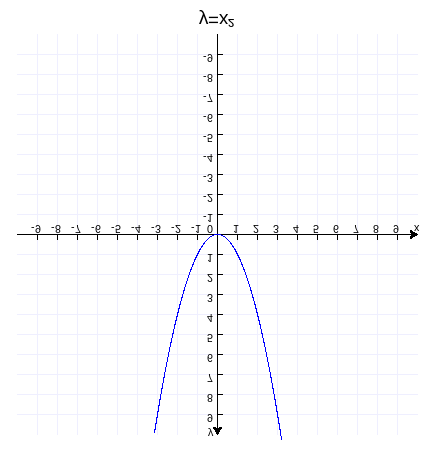
函数的图象就像向空中斜抛物体所走的轨迹，所以把它叫做抛物线。

　　把函数改为y=ax²（a≠0)，a的大小和正负对函数图有什么影响呢？为此，在同一个坐标平面中作y=x²，y=(1/2)x²，y=(1/4)x²，y=-x²，y=-(1/2)x²，y=-(1/4)x²的函数图，作图代码附录3。

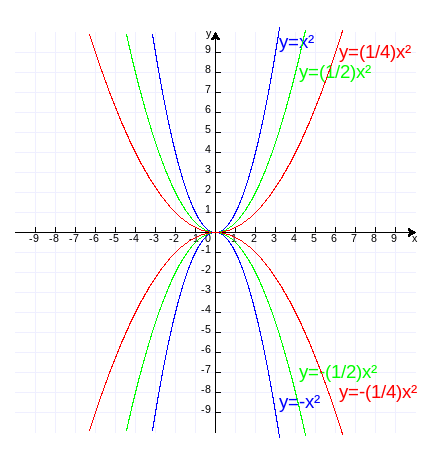
　　可见，a>0，抛物线开口向上，a<0，抛物线开口向下；a的绝对值越大，抛物线的开口越小。

　　自然会想到更一般的二次函数形式y=a(x+b)²+c，函数的图象又会怎样呢？为此，在同一个坐标平面上作图研究。

（１）y=2x²，y=2(x+3)²，y=2(x-3)²，y=-2x²，y=-2(x+3)²，y=-2(x-3)²，作图代码附录4：

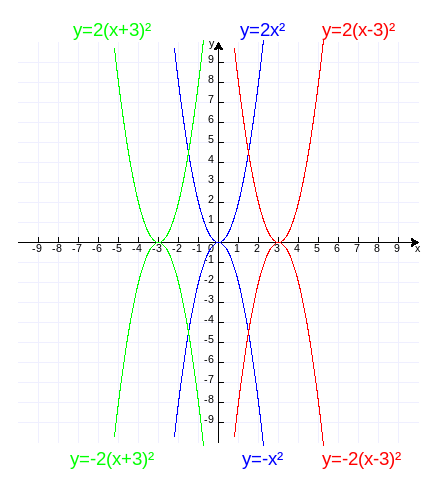
可见，b>0，函数图象向左平移b个单位；b<0，函数图象向右平移-b个单位。

（２）y=2x²，y=2x²+3，y=2x²-3，y=-2x²，y=-2x²+3，y=-2x²-3，作图代码附录5：

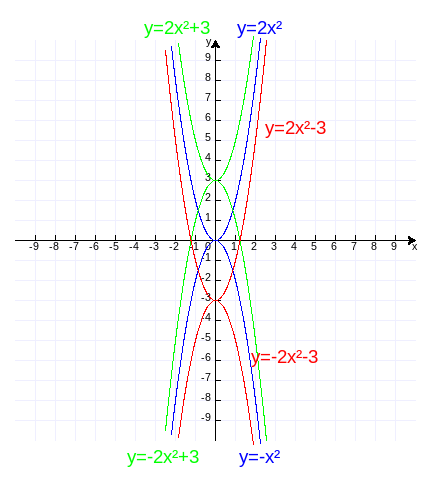
可见，c>0，函数图象向上平移c个单位；c<0，函数图象向下平移-c个单位。

　　例题1：判断下面一元二次函数的开口方向和顶点坐标。

（１）y=2x²+12x+21，

（２）y=2x²+12x+15，

（３）y=2x²-12x+21，

（４）y=2x²-12x+15，

（５）y=-2x²-12x-15，

（６）y=-2x²-12x-21，

（７）y=-2x²+12x-15，

（８）y=-2x²+12x-21。

分析：这是二次函数的一般表达式y=mx²+nx+p，和要用的y=a(x+b)²+c有差别，用配方解决。

解：（１）y=2(x²+6x)+21=2(x²+6x+9-9)+21=2(x+3)²-2×9+21=2(x+3)²+3。

所以函数开口向上，顶点是(-3,3)。

（２）y=2(x²+6x)+15=2(x²+6x+9-9)+15=2(x+3)²-2×9+15=2(x+3)²-3。

所以函数开口向上，顶点是(-3,-3)。

（3）y=2(x²-6x)+21=2(x²-6x+9-9)+21=2(x-3)²-2×9+21=2(x-3)²+3。

所以函数开口向上，顶点是(3,3)。

（4）y=2(x²-6x)+15=2(x²-6x+9-9)+15=2(x-3)²-2×9+15=2(x-3)²-3。

所以函数开口向上，顶点是(3,-3)。

（5）y=-2(x²+6x)-15=-2(x²+6x+9-9)-15=-2(x+3)²+2×9-15=-2(x+3)²+3。

所以函数开口向下，顶点是(-3,3)。

（６）y=-2(x²+6x)-21=-2(x²+6x+9-9)-21=-2(x+3)²+2×9-21=-2(x+3)²-3。

所以函数开口向下，顶点是(-3,-3)。

（7）y=-2(x²-6x)-15=-2(x²-6x+9-9)-15=-2(x-3)²+2×9-15=-2(x-3)²+3。

所以函数开口向上，顶点是(3,3)。

（8）y=-2(x²-6x)-21=-2(x²-6x+9-9)-21=-2(x-3)²+2×9-21=-2(x-3)²-3。

所以函数开口向上，顶点是(3,-3)。

作图验证，代码附录6。

　　对于一元二次函数

y=mx²＋nx+p  (m≠0)，

m是二次项系数，n是一次项系数，p是常数。可通过配方转化

y=m[x²+(n/m)x]+p，

y=m[x²+(n/m)x+(n/2/m)²-(n/2/m)²]+p，

y=m(x+n/2/m)²-m(n/2/m)²+p，

y=m(x+n/2/m)²-n²/4/m+p。

令a=m（二次项系数），b=n/2/m（一次项系数与二次项系数的商的二分之一），c=-n²/4/m+p（b的平方与二次项系数的积的相反数与常数项的和），得

y=a(x+b)²+c。

把m=-2，n=-12，p=-15代入验证

a=-2，b=-12/2/-2=3，c=-(-12)²/4/(-2)-15=18-15=3，

y=-2(x+3)²+3。

　　因此，对于具体的一个二次函数

y=mx²＋nx+p  (m≠0)，

先把它转化为

y=a(x+b)²+c

后再对其进行性质的描述，这样就不用害怕记不住公式了（b的公式最好记住哦）。

　　一元二次函数y=a(x+b)²+c（a≠0）的性质：

（１）函数的图象是一条抛物线；

（２）a>0，开口向上，a<0，开口向下，|a|越大开口越小；

（３）对称轴是x=-b直线；

（４）a>0，当自变量x<-b时，函数值y随x增大而减少，当自变量x>-b时，函数值y随x增大而增大；a<0，当自变量x<-b时，函数值y随x增大而增大，当自变量x>-b时，函数值y随x增大而减少；

（5）函数最大或最小值是c，对称轴x=-b过函数图象的点是顶点，坐标是(-b, c)。

　　例题2：求下面一元二次函数的对称轴、随x增大函数值变化趋势、顶点坐标、最大值或最小值。

（１）y=3x²-12x+5，

（２）y=-2x²+16x-27。

解：（１）b=-12/3/2=-2，对称轴是x=2，x<2时，x增大函数值减少，x>2时，x增大函数值增大。当x=2时函数值最小，y=3×2²-12×2+5=-7，即函数最小值是-7，顶点坐标(2, -7)。

（２）b=16/-2/2=-4，对称轴是x=4，x<4时，x增大函数值增大，x>4时，x增大函数值减少。当x=4时函数值最大，y=-2×4²+16×4-27=5，即函数最大值是5，顶点坐标(4, 5)。

　　作图验证如下，代码附录7。

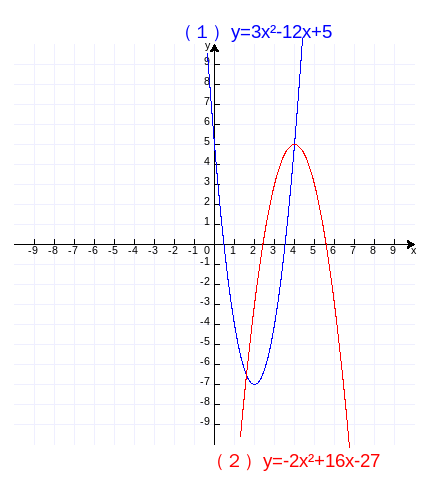
　　例题3：已知直线y=ax+b与过直线外(-1, 7)的抛物线y=mx²+nx+p相交于(-3, -5)和(0, 4)，求这两个函数的解析式。

分析：直线函数y=ax+b有两个字母系数，知道2点坐标，可以列方程组求出这两个系数；抛物线y=mx²+nx+p有三个系数，知道3点坐标，也可以列方程组求出这三个系数。　　

解：（１）直线函数

-3a+b=-5，　　①

b=4。　　②

解得

a=3，

b=4。

直线函数的解析式是

y=3x+4。

（２）抛物线

m-n+p=7，　　①

9m-3n+p=-5，　　②

p=4。　　③

解得

m=-3，

n=-6，

p=4。

抛物线的解析式是

y=-3x²-6x+4。

　　作图验证如下，代码附录8。

　　这种把函数的坐标代进函数列方程组求出系数，从而得到函数解析式的方法叫做待定系数法。

　　练习题1：求下面一元二次函数的对称轴、随x增大函数值变化趋势、顶点坐标、最大值或最小值。

（１）y=2x²＋12x+13，

（２）y=-3x²＋12x-7。

　　练习题2：已知直线y=ax+b与过直线外(3, 1)的抛物线y=mx²+nx+p相交于(-1, 1)和(2, -5)，求这两个函数的解析式。

附录1：

import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)
t.setpos(203,-8)
t.write("2",font=(markFont[0],markFont[1]*2//3,markFont[2]))
#y=x²  
def f(x):
    if x<0:
        return -x
    else:
        return x       
t.setpos(0, -225)
t.write("y=x²",align="center", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f)
t.ht()

附录2：
import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)
#y=x²  
def f(x):
    return x**2      
t.setpos(0, -225)
t.write("y=x²",align="center", font=(markFont[0],14,markFont[2]))
t.pencolor("blue")
trace(t,-10,10,f)
t.ht()

附录3：

import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)
#y=x²  
t.pencolor("blue")
def f(x):
    return x**2      
t.setpos(65, 180)
t.write("y=x²",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f)
#y=-x²  
def f2(x):
    return -x**2      
t.setpos(65, -180)
t.write("y=-x²",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f2)
#y=(1/2)x²  
t.pencolor("green")
def f3(x):
    return Fraction(1,2)*x**2
t.setpos(85, 150)
t.write("y=(1/2)x²",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f3)
#y=-(1/2)x²  
def f4(x):
    return -Fraction(1,2)*x**2      
t.setpos(85, -150)
t.write("y=-(1/2)x²",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f4)
#y=(1/4)x²  
t.pencolor("red")
def f5(x):
    return Fraction(1,4)*x**2
t.setpos(125, 170)
t.write("y=(1/4)x²",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f5)
#y=-(1/4)x²  
def f6(x):
    return -Fraction(1,4)*x**2      
t.setpos(125, -170)
t.write("y=-(1/4)x²",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f6)
t.ht()

附录4：
import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)
#y=2x²  
t.pencolor("blue")
def f(x):
    return 2*x**2      
t.setpos(20*5**0.5, 202)
t.write("y=2x²",align="center", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f)
#y=-2x²  
def f2(x):
    return -2*x**2      
t.setpos(20*5**0.5, -227)
t.write("y=-x²",align="center", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f2)

#y=2(x+3)²  
t.pencolor("green")
def f3(x):
    return 2*(x+3)**2
t.setpos(20*(-5**0.5-3), 202)
t.write("y=2(x+3)²",align="center", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f3)
#y=-2(x+3)²   
def f4(x):
    return -2*(x+3)**2      
t.setpos(20*(-5**0.5-3), -227)
t.write("y=-2(x+3)²",align="center", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f4)
#y=2(x-3)²
t.pencolor("red")
def f5(x):
    return 2*(x-3)**2
t.setpos(20*(5**0.5+3), 202)
t.write("y=2(x-3)²",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f5)
#y=-2(x-3)²
def f6(x):
    return -2*(x-3)**2      
t.setpos(20*(5**0.5+3), -227)
t.write("y=-2(x-3)²",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f6)
t.ht()

附录5：
import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)
#y=2x²  
t.pencolor("blue")
def f(x):
    return 2*x**2      
t.setpos(20*5**0.5, 202)
t.write("y=2x²",align="center", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f)
#y=-2x²  
def f2(x):
    return -2*x**2      
t.setpos(20*5**0.5, -227)
t.write("y=-x²",align="center", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f2)

#y=2x²+3  
t.pencolor("green")
def f3(x):
    return 2*x**2+3
t.setpos(20*(-(7/2)**0.5), 202)
t.write("y=2x²+3",align="center", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f3)
#y=-2x²+3     
def f4(x):
    return -2*x**2+3    
t.setpos(20*(-(13/2)**0.5), -227)
t.write("y=-2x²+3",align="center", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f4)
#y=2x²-3  
t.pencolor("red")
def f5(x):
    return 2*x**2-3
t.setpos(20*(13/2)**0.5, 102)
t.write("y=2x²-3",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f5)
#y=-2x²-3
def f6(x):
    return -2*x**2 - 3     
t.setpos(20*(7/2)**0.5, -127)
t.write("y=-2x²-3",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f6)
t.ht()

附录6：
import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)
#y=2x²+12x+21  
def f(x):
    return 2*x**2+12*x+21     
t.setpos(20*((7/2)**0.5-3), 202)
t.write("y=2x²+12x+21",align="center", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f)
#y=-2x²-12x-15  
def f2(x):
    return -2*x**2-12*x-15       
t.setpos(20*((7/2)**0.5-3), -227)
t.write("y=-2x²-12x-15",align="center", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f2)
#y=2x²+12x+15  
t.pencolor("green")
def f3(x):
    return 2*x**2+12*x+15
t.setpos(20*(-(13/2)**0.5-3), 202)
t.write("y=2x²+12x+15",align="right", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f3)
#y=-2x²-12x-21    
def f4(x):
    return -2*x**2-12*x-21    
t.setpos(20*(-(13/2)**0.5-3), -227)
t.write("y=-2x²-12x-21",align="right", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f4)
#y=2x²-12x+21
t.pencolor("red")
def f5(x):
    return 2*x**2-12*x+21
t.setpos(20*((7/2)**0.5+3), 202)
t.write("y=2x²-12x+21",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f5)
#y=-2x²+12x-15
def f6(x):
    return -2*x**2 +12*x-15     
t.setpos(20*((7/2)**0.5+3), -227)
t.write("y=-2x²+12x-15",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f6)
#y=2x²-12x+15
t.pencolor("blue")
def f7(x):
    return 2*x**2-12*x+15
t.setpos(20*((13/2)**0.5+3), 102)
t.write("y=2x²-12x+15",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f7)
#y=-2x²+12x-21
def f8(x):
    return -2*x**2 +12*x-21     
t.setpos(20*((13/2)**0.5+3), -127)
t.write("y=-2x²+12x-21",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f8)
t.ht()

附录7：
import sys
sys.path.append("/5xstar/pyfiles")
from fractions import Fraction
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)
#（１）y=3x²-12x+5  
t.pencolor("blue")
def f(x):
    return 3*x**2-12*x+5     
t.setpos(20*2, 202)
t.write("（１）y=3x²-12x+5",align="center", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f)
#（２）y=-2x²+16x-27  
t.pencolor("red")
def f2(x):
    return -2*x**2+16*x-27       
t.setpos(20*4, -227)
t.write("（２）y=-2x²+16x-27",align="center", font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f2)
t.ht()

附录8：

import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)
t.setpos(-1*20, 7*20)
t.dot("red")
t.setpos(-3*20, -5*20)
t.dot("blue")
t.setpos(0, 4*20)
t.dot("blue")
#y=3x+4  
t.pencolor("blue")
def f(x):
    return 3*x+4     
t.setpos(40, 140)
t.write("y=3x+4",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f)
#y=-3x²-6x+4  
t.pencolor("red")
def f2(x):
    return -3*x**2-6*x+4       
t.setpos(40, -140)
t.write("y=-3x²-6x+4",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f2)
t.ht()