所谓不等式,就是相应函数的函数值(值域)的一定区间对应的自变量取值区间。因此,为了研究一元二次不等式,还是要回到一元二次函数中来。这里讨论的一元二次不等式对应的一元二次方程都有2不同实数根。
例题1:解下面不等式
x²+4x-12>0。
分析:我们先画y=x²+4x-12的图象,y>0的函数图象对应的x取值范围。下图,作图代码附录1。
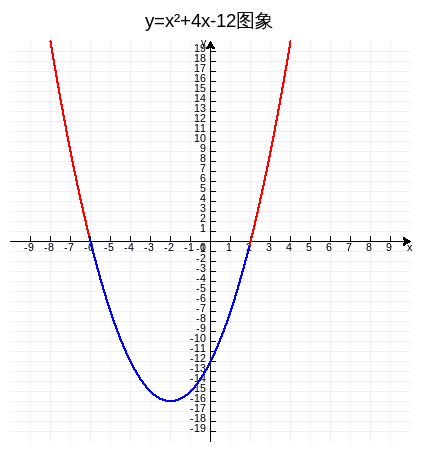
由图可见,x²+4x-12>0的解是方程x²+4x-12=0的两个根之外的部分。
解:解方程
x²+4x-12=0,
(x+2)²-16=0,
得根
x1=-6,x2=2。
所以原不等式的解是
x<-6 或 x>2。
如果把不等式改为x²+4x-12<0,解方程步骤是一样的,最后可得解是
-6<x<2。
如果把不等式中的多项式取反,即改为-x²-4x+12>0。函数y=-x²-4x+12的图象如下图,作图代码附录2。
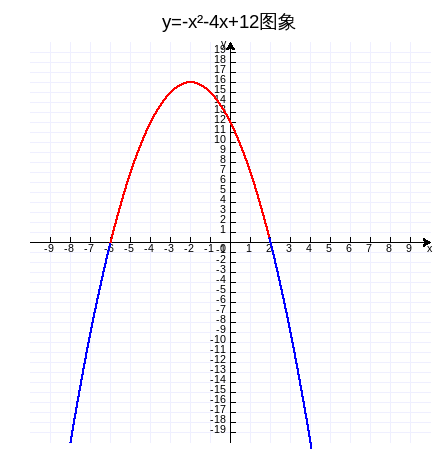
解方程的步骤还是一样的,有图象以x轴为对称轴反过来了,所以不等式的解是
-6<x<2。
如果不等式改为-x²-4x+12<0,同样得解
x<-6 或 x>2。
可见,一元二次方程的两个根把定义域分开3部分,一元二次不等式的解要么是中间部分,要么是两边的2部分,二次系数与不等式同向(同>0或同<0)取两边的2部分,异向取中间部分。
如果上面的规律记不住怎么办?遇到二次系数小于0的情况,根据不等式的性质——同时乘负数改变不等号的方向,化成二次系数大于0的情况,由于二次系数大于0,函数开口向上,显然中间部分小于0,两边2部分大于0。所以,一元二次不等式ax²+bx+c>0(a>0)的解是两边2部分,一元二次不等式ax²+bx+c<0(a>0)的解是中间部分。
上面这种转化方法在解不等式时似乎不太重要,但在解一元二次不等式组时可能就显得重要起来,否则容易掉进逻辑陷进,把简单的题做错了。
例题2:解下面不等式组
x²+2x-8<0, ①
-2x²+8x<0。 ②
解:用不等式的性质,把②转化为
x²-4x>0。 ③
解方程
x²+2x-8=0
(x+1)²-9=0
得根
x1=-4,x2=2,
不等式①的解
-4<x<2。
解方程
x²-4x=0
x(x-4)=0
得根
x1=0,x2=4,
不等式③的解
x<0或x>4。
综合起来,得不等式组的解是
-4<x<0。
作图验证如下,作图代码附录3。

例题3:解不等式组
2|x+1|-7>0, ①
-x²+6x+7>0。 ②
分析:一元一次绝对值不等式与一元二次不等式一样,可以把一元二次不等式的规律直接用于一元一次绝对值不等式。
解:解方程
2|x+1|-7=0
|x+1|=7/2
得解
x1=-(9/2),x2=5/2,
绝对值前系数等同于一元二次不等式的二次系数,所以这个不等式的解
x<-(9/2)或x>5/2。
把②转化为
x²-6x-7<0,③
解③对应的方程
x²-6x-7=0,
(x+1)(x-7)=0
得两个根
x1=-1,x2=7。
不等式③的解(也是②的解)
-1<x<7。
可见原不等式的解是
5/2<x<7。
作图验证如下,作图代码附录4。
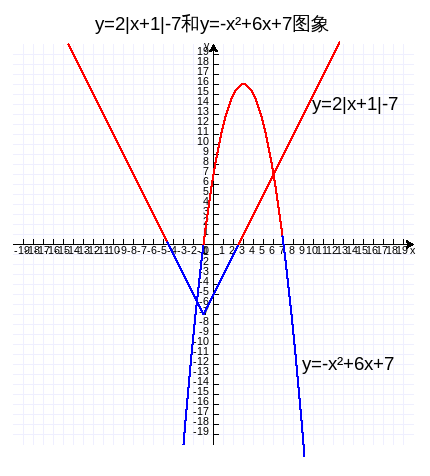
例题4:解不等式组
2x+3>0, ①
-(1/2)x²+2x+6>0。 ②
解:解①得
x>-3/2。
解②对应的方程
-(1/2)x²+2x+6=0
x²-4x-12=0
(x+2)(x-6)=0
得根
x1=-2,x2=6,
得②的解
-2<x<6。
所以不等式组的解是
-3/2<x<6。
作图验证如下,作图代码附录5。

练习题1:解下面不等式组
(1)
2x-5<0
6x²-x-10<0
(2)
4x²+4x-15>0
-x²+10x+11>0
(3)
3|x-2|-8>0
-(1/2)x²-2x+16>0
附录1:
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t,yUnt=(1,10))
#标题
t.setpos(0, 210)
t.write("y=x²+4x-12图象",align="center",font=(markFont[0],14,markFont[2]))
#y=x²+4x-12
t.pensize(2)
def f(x):
_temp=x**2+4*x-12
if _temp>0:
t.pencolor("red")
else:
t.pencolor("blue")
return _temp
trace(t,-10,10,f)
t.ht()
附录2:
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t,yUnt=(1,10))
#标题
t.setpos(0, 210)
t.write("y=-x²-4x+12图象",align="center",font=(markFont[0],14,markFont[2]))
#y=-x²-4x+12
t.pensize(2)
def f(x):
_temp=-x**2-4*x+12
if _temp>0:
t.pencolor("red")
else:
t.pencolor("blue")
return _temp
trace(t,-10,10,f)
t.ht()
附录3:
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t, yUnt=(1,10))
t.pensize(2)
#标题与函数解析式
t.setpos(0, 210)
t.write("y=x²+2x-8和y=-2x²+8x图象",align="center",font=(markFont[0],14,markFont[2]))
t.setpos(70, 70)
t.write("y=x²+2x-8",font=(markFont[0],14,markFont[2]))
t.setpos(110, -100)
t.write("y=-2x²+8x",font=(markFont[0],14,markFont[2]))
#y=x²+2x-8
def f(x):
_temp=x**2+2*x-8
if _temp>0:
t.pencolor("red")
else:
t.pencolor("blue")
return _temp
trace(t,-10,10,f)
#y=-2x²+8x
def f2(x):
_temp=-2*x**2+8*x
if _temp>0:
t.pencolor("red")
else:
t.pencolor("blue")
return _temp
trace(t,-10,10,f2)
t.ht()
附录4:
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t, xUnt=(1,10), yUnt=(1,10))
t.pensize(2)
#标题与函数解析式
t.setpos(0, 210)
t.write("y=2|x+1|-7和y=-x²+6x+7图象",align="center",font=(markFont[0],14,markFont[2]))
t.setpos(100, 130)
t.write("y=2|x+1|-7",font=(markFont[0],14,markFont[2]))
t.setpos(90, -130)
t.write("y=-x²+6x+7",font=(markFont[0],14,markFont[2]))
#y=2|x+1|-7
def f(x):
_temp=2*abs(x+1)-7
if _temp>0:
t.pencolor("red")
else:
t.pencolor("blue")
return _temp
trace(t,-20,20,f)
#y=-x²+6x+7
def f2(x):
_temp=-x**2+6*x+7
if _temp>0:
t.pencolor("red")
else:
t.pencolor("blue")
return _temp
trace(t,-20,20,f2)
t.ht()
附录5:
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t, xUnt=(1,10), yUnt=(1,10))
t.pensize(2)
#标题与函数解析式
t.setpos(0, 210)
t.write("y=2x+3和y=-(1/2)x²+2x+6图象",align="center",font=(markFont[0],14,markFont[2]))
t.setpos(60, 130)
t.write("y=2x+3",font=(markFont[0],14,markFont[2]))
t.setpos(60, -90)
t.write("y=-(1/2)x²+2x+6",font=(markFont[0],14,markFont[2]))
#y=2x+3
def f(x):
_temp=2*x+3
if _temp>0:
t.pencolor("red")
else:
t.pencolor("blue")
return _temp
trace(t,-20,20,f)
#y=-(1/2)x²+2x+6
def f2(x):
_temp=-x**2/2+2*x+6
if _temp>0:
t.pencolor("red")
else:
t.pencolor("blue")
return _temp
trace(t,-20,20,f2)
t.ht()
附录5:
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t, xUnt=(1,10), yUnt=(1,10))
t.pensize(2)
#标题与函数解析式
t.setpos(0, 210)
t.write("y=2x+3和y=-(1/2)x²+2x+6图象",align="center",font=(markFont[0],14,markFont[2]))
t.setpos(60, 130)
t.write("y=2x+3",font=(markFont[0],14,markFont[2]))
t.setpos(75, -40)
t.write("y=-(1/2)x²+2x+6",font=(markFont[0],14,markFont[2]))
#y=2x+3
def f(x):
_temp=2*x+3
if _temp>0:
t.pencolor("red")
else:
t.pencolor("blue")
return _temp
trace(t,-20,20,f)
#y=-(1/2)x²+2x+6
def f2(x):
_temp=-x**2/2+2*x+6
if _temp>0:
t.pencolor("red")
else:
t.pencolor("blue")
return _temp
trace(t,-20,20,f2)
t.ht()