把正比例函数

y=x

或

y=-x

的x换成1/x就成了反比例函数

y=1/x　(x≠0)

或

y=-1/x　(x≠0)。

　　为了研究反比例函数的性质，先把上面四个函数图作出来。如下2图，作图代码附录1、2。

　　比例常数绝对值大于1的情况，如下2图，作图代码附录3、4。

　　不失一般性，我们研究y=1/x(x>0)的情况。当x越大时，1/x就越接近0，但还是不等于0，0是一个不可达到的界限。这种情况与一元二次函数的最大最小值有差别。最大最小值也是一种界限，但函数是可以达到这个值的。为了说明反比例函数的这种特性，我们扩充最值的概念为有界性。有最值一定是有界性，是有界性不一定有最值。

　　一般地，反比例函数y=k/x(x≠0)的图象是双曲线，它具有以下性质：

（１）当k>0时，双曲线的两支分别位于第一、第三象限，在每一个象限内，y随x的增大而减小，都是单调减区间（注意，由于第一象限的函数值都比第三象限的大，在整个定义域内不是减函数）。第一象限函数的下界值是0，无上界值；第三象限函数的上界值是0，无下界值。每个象限内都是轴对称图形，对称轴是y=x；2个象限的图形轴对称（对称轴是y=-x）和中心对称（对称中心是原点）。

（２）当k<0时，双曲线的两支分别位于第二、第四象限，在每一个象限内，y随x的增大而增大，都是单调增区间（注意，由于第二象限的函数值都比第四象限的大，在整个定义域内不是增函数）。第二象限函数的下界值是0，无上界值；第四象限函数的上值界是0，无下界值。每个象限内都是轴对称图形，对称轴是y=-x；2个象限的图形轴对称（对称轴是y=x）和中心对称（对称中心是原点）。

（３）当k的绝对值越大，图象远离坐标轴，反之，靠近坐标轴。

　　反比例函数增加一个常数项q

y=k/x+q

函数的图象会怎样呢？用y=6/x和y=6/x+2比较看看，图如下，作图代码附录5。

可见，常数项不改变双曲线的形状，只向上平移了2个单位。对于函数

y=k/x+q

的图象，当q>0时，是y=k/x的图象向上平移q个单位；当q<0时，是y=k/x的图象向下平移|q|个单位。

　　反比例函数的分母中增加一个常数项p

y=k/(x+p)

函数的图象会怎样呢？用y=6/x和y=6/(x+3)比较看看，图如下，作图代码附录6。

可见，分母中的常数项也不改变双曲线的形状，只向左平移了3个单位。对于函数

y=k/(x+p)

的图象，当p>0时，是y=k/x的图象向左平移p个单位；当p<0时，是y=k/x的图象向右平移|p|个单位。

　　由于k/(ax+p) (a≠0)等于(k/a)/[a+(p/a)]，所以扩充后的反比例函数，为了方便起见，这里给它起个名——一元一次分式函数，它的一般式

y=k/(x+p)+q。

　　我们把反比例函数y=1/x和y=-1/x的x用x²代替，就成了"二次反比例函数”

y=1/x²　(x≠0)，

y=-1/x²　(x≠0)。

　　函数的图象如下2图，作图代码附录7、8。

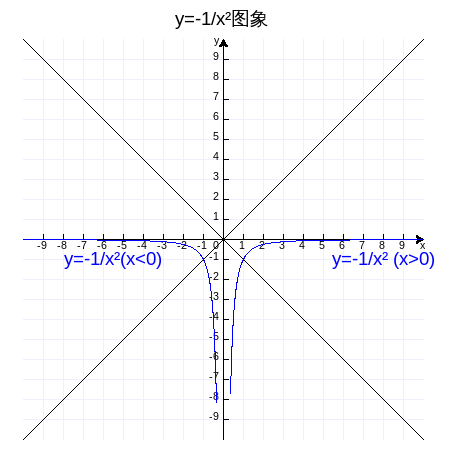
　　函数y=6/x²和y=-6/x²的图象如下2图，作图代码附录9、10。

　　一般地，二次反比例函数y=k/x²(x≠0)的图象是两条曲线（注意：不是双曲线），它具有以下性质：

（１）当k>0时，两条曲线分别位于第一、第二象限，在第一象限内，y随x的增大而减小，即是单调减区间；在第二个象限内，y随x的增大而增大，即是单调增区间。每个象限函数的下值界是0，无上界值。每个象限内都不是轴对称图形，象悬崖；2个象限的图形轴对称（对称轴是y轴）。

（２）当k<0时，两条曲线分别位于第三、第四象限，在第三象限内，y随x的增大而减小，即是单调减区间；在第四象限内，y随x的增大而增大，即是单调增区间。每个象限函数的上值界是0，无下界值。每个象限内都不是轴对称图形，象悬崖；2个象限的图形轴对称（对称轴是y轴）。

（３）当k的绝对值越大，图象远离坐标轴，反之，靠近坐标轴。

　　二次反比例函数增加一个常数项q

y=k/x²+q

函数的图象会怎样呢？用y=6/x²和y=6/x²+2比较看看，图如下，作图代码附录11。

可见，常数项不改变函数图象曲线的形状，只向上平移了2个单位。对于函数

y=k/x²+q

的图象，当q>0时，是y=k/x的图象向上平移q个单位；当q<0时，是y=k/x的图象向下平移|q|个单位。

　　二次反比例函数的分母（平方内）中增加一个常数项p

y=k/(x+p)²

函数的图象会怎样呢？用y=6/x²和y=6/(x+3)²比较看看，图如下，作图代码附录12。

可见，分母（平方内）中的常数项也不改变双曲线的形状，只向左平移了3个单位。对于函数

y=k/(x+p)²

的图象，当p>0时，是y=k/x的图象向左平移p个单位；当p<0时，是y=k/x的图象向右平移|p|个单位。

　　二次反比例函数的分母（平方外）中增加一个常数项r

y=k/(x²+r)

函数的图象会怎样呢？用y=6/x²、y=6/(x²+4)和y=6/(x²-4)比较看看，图如下2图，作图代码附录13、14。

　　可见，分母（平方外）增加一个不为0的常数

y=k/(x²+r)，

完全改变函数的图象：

（１）当r>0时，是以(0,k/r)为顶点、以y轴为对称轴的连续曲线。

（２）当r<0时，函数分为3段，左右两段以y=k/x²比较像，以y轴为对称轴，距离拉开2倍根号r的距离；中间一段是以(0,k/r)为顶点、以y轴为对称轴的开口曲线。

　　为了方便起见，这里给上这些函数起个名——一元二次分式函数，它的一般式

y=k/[(x+p)²+r]+q。

　　练习题1：如果把函数

y=k/|x|

称作绝对值反比例函数，绘制它的图象，k值至少有正不同2个数和负不同2个数（例如：1, 6, -1, -6），仿造本文对反比例函数的归纳方法，归纳绝对值反比例函数的性质。和文本一样，对拓展y=k/|x|+q和y=k/|x+p|进行讨论。

附录1：

import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("反比例函数图象",align="center",font=(markFont[0],14,markFont[2]))

#y=x
t.setpos(120, 100)
t.write("y=x",font=(markFont[0],14,markFont[2]))
t.setpos(-100, -100)
t.write("y=x", align="right", font=(markFont[0],14,markFont[2]))
t.setpos(-200,-200)
t.seth(45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=-x
t.setpos(110, -100)
t.write("y=-x",font=(markFont[0],14,markFont[2]))
t.setpos(-120, 100)
t.write("y=-x", align="right", font=(markFont[0],14,markFont[2]))
t.setpos(-200,200)
t.seth(-45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=k/x
k=1
def f(x):
    return k/x
t.pencolor("red")
#y=1/x (x>0)
t.setpos(110, 10)
t.write("y=1/x(x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.1,10.1,f)
#y=1/x (x<0)
t.setpos(-60, -30)
t.write("y=1/x(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.09,f)
t.ht()

附录2：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("反比例函数图象",align="center",font=(markFont[0],14,markFont[2]))

#y=x
t.setpos(120, 100)
t.write("y=x",font=(markFont[0],14,markFont[2]))
t.setpos(-100, -100)
t.write("y=x", align="right", font=(markFont[0],14,markFont[2]))
t.setpos(-200,-200)
t.seth(45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=-x
t.setpos(110, -100)
t.write("y=-x",font=(markFont[0],14,markFont[2]))
t.setpos(-120, 100)
t.write("y=-x", align="right", font=(markFont[0],14,markFont[2]))
t.setpos(-200,200)
t.seth(-45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=k/x
k=-1
def f(x):
    return k/x
t.pencolor("blue")
#y=-1/x (x>0)
t.setpos(110, -30)
t.write("y=-1/x(x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.1,10.1,f)
#y=-1/x (x<0)
t.setpos(-60, 10)
t.write("y=-1/x(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.09,f)

t.ht()

附录3：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("反比例函数图象",align="center",font=(markFont[0],14,markFont[2]))

#y=x
t.setpos(120, 100)
t.write("y=x",font=(markFont[0],14,markFont[2]))
t.setpos(-100, -100)
t.write("y=x", align="right", font=(markFont[0],14,markFont[2]))
t.setpos(-200,-200)
t.seth(45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=-x
t.setpos(110, -100)
t.write("y=-x",font=(markFont[0],14,markFont[2]))
t.setpos(-120, 100)
t.write("y=-x", align="right", font=(markFont[0],14,markFont[2]))
t.setpos(-200,200)
t.seth(-45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=k/x
k=6
def f(x):
    return k/x
t.pencolor("red")
#y=6/x (x>0)
t.setpos(110, 30)
t.write("y=6/x(x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.1,10.1,f)
#y=6/x (x<0)
t.setpos(-60, -55)
t.write("y=6/x(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.09,f)
t.ht()

附录4：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("反比例函数图象",align="center",font=(markFont[0],14,markFont[2]))

#y=x
t.setpos(120, 100)
t.write("y=x",font=(markFont[0],14,markFont[2]))
t.setpos(-100, -100)
t.write("y=x", align="right", font=(markFont[0],14,markFont[2]))
t.setpos(-200,-200)
t.seth(45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=-x
t.setpos(110, -100)
t.write("y=-x",font=(markFont[0],14,markFont[2]))
t.setpos(-120, 100)
t.write("y=-x", align="right", font=(markFont[0],14,markFont[2]))
t.setpos(-200,200)
t.seth(-45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=k/x
k=-6
def f(x):
    return k/x
t.pencolor("blue")
#y=-6/x (x>0)
t.setpos(110, -55)
t.write("y=-6/x(x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.1,10.1,f)
#y=-6/x (x<0)
t.setpos(-60, 40)
t.write("y=-6/x(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.09,f)
t.ht()

附录5：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("y=6/x和y=6/x+2图象",align="center",font=(markFont[0],14,markFont[2]))

#y=x
t.setpos(-200,-200)
t.seth(45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=-x
t.setpos(-200,200)
t.seth(-45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=2
t.setpos(-200,40)
t.seth(0)
tmp=0
while tmp<405:
    tmp+=5
    t.down()
    t.fd(2.5)
    t.up()
    t.fd(2.5)
lth=360*2**0.5
#y=x+2
t.setpos(-200,-160)
t.seth(45)
tmp=0
while tmp<lth:
    tmp+=5
    t.down()
    t.fd(2.5)
    t.up()
    t.fd(2.5)
#y=-x+2
t.setpos(-160,200)
t.seth(-45)
tmp=0
while tmp<lth:
    tmp+=5
    t.down()
    t.fd(2.5)
    t.up()
    t.fd(2.5)
t.up()   

#y=k/x
k=6
q=0
def f(x):
    return k/x+q
t.pencolor("red")
#y=6/x (x>0)
t.setpos(110, 30)
t.write("y=6/x(x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.1,10.1,f)
#y=6/x (x<0)
t.setpos(-60, -55)
t.write("y=6/x(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.09,f)

t.pencolor("blue")
q=2
#y=6/x +2(x>0)
t.setpos(110, 70)
t.write("y=6/x+2(x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.1,10.1,f)
#y=6/x +2(x<0)
t.setpos(-60, -15)
t.write("y=6/x+2(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.09,f)
t.ht()

附录6：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("y=6/x和y=6/(x+3)图象",align="center",font=(markFont[0],14,markFont[2]))

#y=x
t.setpos(-200,-200)
t.seth(45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=-x
t.setpos(-200,200)
t.seth(-45)
t.down()
t.fd(400*2**0.5)
t.up()
#x=-3
t.setpos(-60,-200)
t.seth(90)
tmp=0
while tmp<405:
    tmp+=5
    t.down()
    t.fd(2.5)
    t.up()
    t.fd(2.5)
lth=320*2**0.5
#y=x+3
t.setpos(-200,-140)
t.seth(45)
tmp=0
while tmp<lth:
    tmp+=5
    t.down()
    t.fd(2.5)
    t.up()
    t.fd(2.5)
#x=-x+3
t.setpos(-200,140)
t.seth(-45)
tmp=0
while tmp<lth:
    tmp+=5
    t.down()
    t.fd(2.5)
    t.up()
    t.fd(2.5)
t.up()   

#y=k/x
k=6
p=0
def f(x):
    return k/(x+p)
t.pencolor("red")
#y=6/x (x>0)
t.setpos(110, 30)
t.write("y=6/x(x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.1,10.1,f)
#y=6/x (x<0)
t.setpos(-60, -55)
t.write("y=6/x(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.09,f)

t.pencolor("blue")
p=3
#y=6/(x +3)(x>-3)
t.setpos(110, 90)
t.write("y=6/(x+3)(x>-3)",font=(markFont[0],14,markFont[2]))
trace(t,-2.9,10.1,f)
#y=6/(x +3)(x<-3)
t.setpos(-60, 45)
t.write("y=6/(x+3)(x<-3)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-3.1,f)
t.ht()

附录7：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("y=1/x²图象",align="center",font=(markFont[0],14,markFont[2]))

#y=x
t.setpos(-200,-200)
t.seth(45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=-x
t.setpos(-200,200)
t.seth(-45)
t.down()
t.fd(400*2**0.5)
t.up()

#y=k/x²
k=1
def f(x):
    return k/x**2
t.pencolor("red")
#y=1/x² (x>0)
t.setpos(110, 10)
t.write("y=1/x² (x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.01,10.1,f)
#y=1/x² (x<0)
t.setpos(-60, 10)
t.write("y=1/x²(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.35,f)
t.ht()

附录8：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("y=-1/x²图象",align="center",font=(markFont[0],14,markFont[2]))

#y=x
t.setpos(-200,-200)
t.seth(45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=-x
t.setpos(-200,200)
t.seth(-45)
t.down()
t.fd(400*2**0.5)
t.up()

#y=k/x²
k=-1
def f(x):
    return k/x**2
t.pencolor("blue")
#y=-1/x² (x>0)
t.setpos(110, -30)
t.write("y=-1/x² (x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.01,10.1,f)
#y=1/x² (x<0)
t.setpos(-60, -30)
t.write("y=-1/x²(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.35,f)
t.ht()

附录9：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("y=6/x²图象",align="center",font=(markFont[0],14,markFont[2]))

#y=x
t.setpos(-200,-200)
t.seth(45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=-x
t.setpos(-200,200)
t.seth(-45)
t.down()
t.fd(400*2**0.5)
t.up()

#y=k/x²
k=6
def f(x):
    return k/x**2
t.pencolor("red")
#y=6/x² (x>0)
t.setpos(110, 15)
t.write("y=6/x² (x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.01,10.1,f)
#y=6/x² (x<0)
t.setpos(-60, 15)
t.write("y=6/x²(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.35,f)
t.ht()

附录10：

import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("y=-6/x²图象",align="center",font=(markFont[0],14,markFont[2]))

#y=x
t.setpos(-200,-200)
t.seth(45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=-x
t.setpos(-200,200)
t.seth(-45)
t.down()
t.fd(400*2**0.5)
t.up()

#y=k/x²
k=-6
def f(x):
    return k/x**2
t.pencolor("blue")
#y=-6/x² (x>0)
t.setpos(110, -35)
t.write("y=-6/x² (x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.01,10.1,f)
#y=-6/x² (x<0)
t.setpos(-60, -35)
t.write("y=-6/x²(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.35,f)
t.ht()

附录11：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("y=6/x²和y=6/x²+2图象",align="center",font=(markFont[0],14,markFont[2]))

t.pencolor("blue")
#y=x
t.setpos(-200,-200)
t.seth(45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=-x
t.setpos(-200,200)
t.seth(-45)
t.down()
t.fd(400*2**0.5)
t.up()

#y=k/x²
k=6
q=0
def f(x):
    return k/x**2+q
#y=6/x² (x>0)
t.setpos(110, 15)
t.write("y=6/x² (x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.01,10.1,f)
#y=6/x² (x<0)
t.setpos(-60, 15)
t.write("y=6/x²(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.35,f)

t.pencolor("red")
t.setpos(-200,40)
t.seth(0)
for i in range(-200,201,5):
    t.down()
    t.fd(2.5)
    t.up()
    t.fd(2.5)
#y=x+2
t.setpos(-200,-160)
t.seth(45)
tmp=0
while tmp<360*2**0.5:
    tmp+=5
    t.down()
    t.fd(2.5)
    t.up()    
    t.fd(2.5)
#y=-x+2
t.setpos(-160,200)
t.seth(-45)
tmp=0
while tmp<360*2**0.5:
    tmp+=5
    t.down()
    t.fd(2.5)
    t.up()    
    t.fd(2.5)

q=2
#y=6/x² +2(x>0)
t.setpos(110, 55)
t.write("y=6/x² +2(x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.01,10.1,f)
#y=6/x² +2(x<0)
t.setpos(-60, 55)
t.write("y=6/x²+2(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.35,f)
t.ht()

附录12：

import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("y=6/x²和y=6/(x+3)²图象",align="center",font=(markFont[0],14,markFont[2]))

t.pencolor("blue")
#y=x
t.setpos(-200,-200)
t.seth(45)
t.down()
t.fd(400*2**0.5)
t.up()
#y=-x
t.setpos(-200,200)
t.seth(-45)
t.down()
t.fd(400*2**0.5)
t.up()

#y=k/x²
k=6
p=0
def f(x):
    return k/(x+p)**2
#y=6/x² (x>0)
t.setpos(110, 15)
t.write("y=6/x² (x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.01,10.1,f)
#y=6/x² (x<0)
t.setpos(-60, 15)
t.write("y=6/x²(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.35,f)

t.pencolor("red")
t.setpos(-60,-200)
t.seth(90)
for i in range(-200,201,5):
    t.down()
    t.fd(2.5)
    t.up()
    t.fd(2.5)
#y=x+3
t.setpos(-200,-140)
t.seth(45)
tmp=0
while tmp<340*2**0.5:
    tmp+=5
    t.down()
    t.fd(2.5)
    t.up()    
    t.fd(2.5)
#y=-x-3
t.setpos(-200,140)
t.seth(-45)
tmp=0
while tmp<340*2**0.5:
    tmp+=5
    t.down()
    t.fd(2.5)
    t.up()    
    t.fd(2.5)

p=3
#y=6/(x+3)² (x>-3)
t.setpos(50, 35)
t.write("y=6/(x+3)²(x>-3)",font=(markFont[0],14,markFont[2]))
trace(t,-2.95,10.1,f)
#y=6/(x+3)²(x<-3)
t.setpos(-120, 35)
t.write("y=6/(x+3)²(x<-3)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-3.05,f)
t.ht()

附录13：

import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("y=6/x²和y=6/x²+4图象",align="center",font=(markFont[0],14,markFont[2]))

#y=k/x²
k=6
r=0
def f(x):
    return k/(x**2+r)
    
t.pencolor("blue")
#y=6/x² (x>0)
t.setpos(110, 15)
t.write("y=6/x² (x>0)",font=(markFont[0],14,markFont[2]))
trace(t,0.01,10.1,f)
#y=6/x² (x<0)
t.setpos(-60, 15)
t.write("y=6/x²(x<0)",align="right",font=(markFont[0],14,markFont[2]))
trace(t,-10,-0.35,f)

t.pencolor("red")
r=4
#y=6/(x²+4)
t.setpos(50, 35)
t.write("y=6/(x²+4)",font=(markFont[0],14,markFont[2]))
trace(t,-10,10,f)
t.ht()

附录14：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)

#标题与函数解析式
t.setpos(0, 210)
t.write("y=6/(x²-4)图象",align="center",font=(markFont[0],14,markFont[2]))

#y=k/x²
k=6
r=-4
def f(x):
    return k/(x**2+r)

t.pencolor("red")
#y=6/(x²-4)(x<-2)
t.setpos(-120, 15)
t.write("x<-2",align="center",font=(markFont[0],14,markFont[2]))
trace(t,-10,-2.05,f)
t.setpos(0, 55)
t.write("-2<x<2",align="center",font=(markFont[0],14,markFont[2]))
trace(t,-2.05,2,f)
t.setpos(120, 15)
t.write("x>2",align="center",font=(markFont[0],14,markFont[2]))
trace(t,2.01,10,f)

t.ht()