一元一次函数
y=2x+4, ①
现要倒过来,y是自变量,x是函数值,得
x=(1/2)y-2 ②
用x作为自变量,y作为函数值,得
y=(1/2)x-2 ③
就是函数①的逆函数。
同理,一元一次函数
y=x+6 ④
的逆函数是
y=x-6; ⑤
一元一次函数
y=-2x+4 ⑥
的逆函数是
y=-(1/2)x+2。⑦
一元一次函数
y=-x+6 ⑧
的逆函数也是
y=-x+6 ⑧
不难发现,原函数是它的逆函数的逆函数。
现在,在同一坐标平面上作①、③、④、⑤、⑥、⑦、⑧的图象如下,作图代码附录1。

从这些一元一次函数y=ax+b(a≠0)与它的逆函数y=(1/a)x-b/a图象中,得出一元一次函数的逆函数性质:
(1)当a=1:b=0时(即y=x)逆函数是它的本身,b≠0时逆函数是它以y=x轴对称的平行线。
(2)当a=-1时,逆函数总是它的本身,并与y=x垂直。
(3)当a≠±1时,逆函数是它以y=x轴对称的相交线(交点在y=x上)。
反比例函数
y=1/x(x≠0) ①
y=-1/x(x≠0) ②
的逆函数也是它本身
y=1/x(x≠0) ①
y=-1/x(x≠0) ②
在同一个坐标平面中把这两个函数描绘出来,如下图,作图代码附录2。
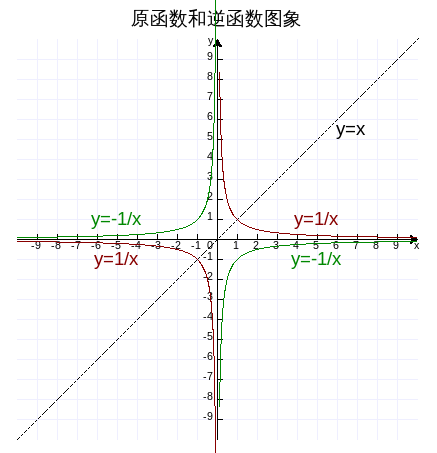
由于反比例函数是以y=x为对称轴的轴对称图形,所以逆函数是本身。
一元一次分式函数
y=2/x+4 ③
的逆函数
y=2/(x-4) ④
在同一个坐标平面中把这两个函数描绘出来,如下图,作图代码附录3。
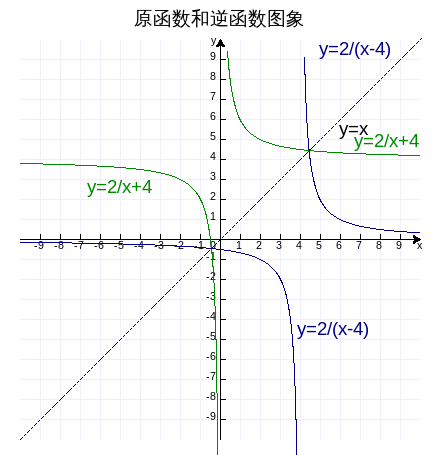
可见,逆函数的两部分分别对称于原函数的两部分。
一元一次分式函数
y=2/(x+4)-5 ⑤
的逆函数
y=2/(x+5)-4 ⑥
在同一个坐标平面中把这两个函数描绘出来,如下图,作图代码附录4。
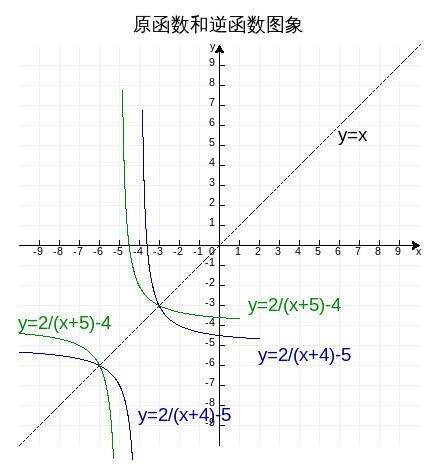
可见,逆函数的两部分也分别对称于原函数的两部分。
一元一次分式函数
y=-2/(x+4)+3 ⑦
的逆函数
y=-2/(x-3)-4 ⑧
在同一个坐标平面中把这两个函数描绘出来,如下图,作图代码附录5。
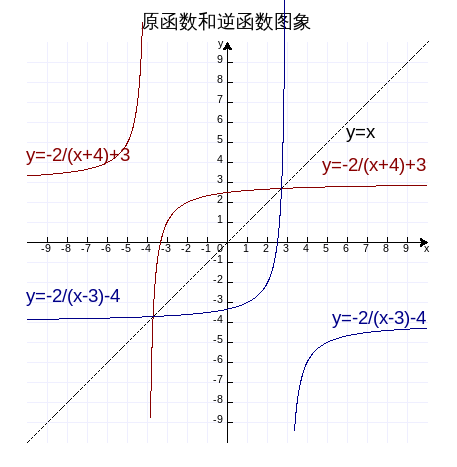
可见,逆函数的两部分也分别对称于原函数的两部分。
从这些一元一次分式函数y=k/(x+p)+q(k≠0)与它的逆函数y=k/(x-q)-p图象中,得出一元一次分式函数的逆函数性质:
(1)当p=0和q=0时(即反比例函数)逆函数是它的本身。
(2)其它情况,逆函数是它以y=x轴对称的图形,如有交点必在y=x上。
一元一次函数是单调函数,一元一次分式函数不是单调函数,但它们有一个共同的特点——自变量与函数值一一对应。就因为这一点所以都有逆函数。这种有逆函数的函数叫做可逆函数。
自变量值与函数值一一对应的函数是可逆的函数;一个函数可逆,则它的自变量值与函数值一一对应。
例题1:根据下面的函数解析式,判断函数是否可逆。如不注明定义域,则定义域是实数。
(1)y=5x+19,
(2)y=3|x-2|-1,
(3)y=5/(x+2)-7 x≠-2,
(4)y=2x²,
(5)y=x² (x为正整数),
(6)y=4x²+4x-5。
解:
(1)自变量值与函数值一一对应,可逆。
(2)x=0和x=4函数值都是5,不可逆。
(3)自变量值与函数值一一对应,可逆。
(4)x=1和x=-1函数值都是2,不可逆。
(5)自变量值与函数值一一对应,可逆。
(6)x=-1和x=0函数值都是-5,不可逆。
练习题1:根据下面的函数解析式,判断函数是否可逆。如不注明定义域,则定义域是实数。
(1)y=-5x²,
(2)y=3x² (x为负整数),
(3)y=x²-2x-3,
(4)y=2x+7,
(5)y=5|-x+4|-3,
(6)y=3/(x-4)+5 (x≠4),
(7)y=x·(x+1) (x≥-1的整数)。注:点(·)是×运行。
附录1:
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t,)
#标题与函数解析式
t.setpos(0, 210)
t.write("原函数和逆函数图象",align="center",font=(markFont[0],14,markFont[2]))
#对称轴
t.setpos(-200,-200)
t.seth(45)
tmp=0
while tmp<400*2**.5+1:
t.down()
t.fd(2.5)
t.up()
t.fd(2.5)
tmp+=5
t.setpos(120,100)
t.write("y=x",font=(markFont[0],14,markFont[2]))
t.pencolor("red")
#y=2x+4
def f(x):
return 2*x+4
trace(t,-10,10.1,f)
t.setpos(50,160)
t.write("y=2x+4",font=(markFont[0],14,markFont[2]))
#y=(1/2)x-2
def f2(x):
return x/2-2
trace(t,-10,10.1,f2)
t.setpos(30,-50)
t.write("y=(1/2)x-2",font=(markFont[0],14,markFont[2]))
t.pencolor("blue")
#y=x+6
def f3(x):
return x+6
trace(t,-10,10.1,f3)
t.setpos(-50,80)
t.write("y=x+6",align="right",font=(markFont[0],14,markFont[2]))
#y=x-6
def f4(x):
return x-6
trace(t,-10,10.1,f4)
t.setpos(-50,-160)
t.write("y=x-6",align="right",font=(markFont[0],14,markFont[2]))
t.ht()
附录2:
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t,)
#标题与函数解析式
t.setpos(0, 210)
t.write("原函数和逆函数图象",align="center",font=(markFont[0],14,markFont[2]))
#对称轴
t.setpos(-200,-200)
t.seth(45)
tmp=0
while tmp<400*2**.5+1:
t.down()
t.fd(2.5)
t.up()
t.fd(2.5)
tmp+=5
t.setpos(120,100)
t.write("y=x",font=(markFont[0],14,markFont[2]))
t.pencolor("#880000")
#y=1/x
def f(x):
return 1/x
trace(t,-10,-0.02,f)
trace(t,0.02,10,f)
t.setpos(100,10)
t.write("y=1/x",align="center",font=(markFont[0],14,markFont[2]))
t.setpos(-100,-30)
t.write("y=1/x",align="center",font=(markFont[0],14,markFont[2]))
t.pencolor("#008800")
#y=-1/x
def f2(x):
return -1/x
trace(t,-10,-0.02,f2)
trace(t,0.02,10.02,f2)
t.setpos(-100,10)
t.write("y=-1/x",align="center",font=(markFont[0],14,markFont[2]))
t.setpos(100,-30)
t.write("y=-1/x",align="center",font=(markFont[0],14,markFont[2]))
t.ht()
附录3:
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t,)
#标题与函数解析式
t.setpos(0, 210)
t.write("原函数和逆函数图象",align="center",font=(markFont[0],14,markFont[2]))
#对称轴
t.setpos(-200,-200)
t.seth(45)
tmp=0
while tmp<400*2**.5+1:
t.down()
t.fd(2.5)
t.up()
t.fd(2.5)
tmp+=5
t.setpos(120,100)
t.write("y=x",font=(markFont[0],14,markFont[2]))
t.pencolor("#008800")
#y=2/x+4
def f3(x):
return 2/x+4
trace(t,-10,-0.02,f3)
trace(t,0.02,10.02,f3)
t.setpos(200,88)
t.write("y=2/x+4",align="right",font=(markFont[0],14,markFont[2]))
t.setpos(-100,42)
t.write("y=2/x+4",align="center",font=(markFont[0],14,markFont[2]))
#y=2/(x-4)
t.pencolor("#000088")
def f4(x):
return 2/(x-4)
trace(t,-10,3.98,f4)
trace(t,4.02,10.02,f4)
t.setpos(150,-100)
t.write("y=2/(x-4)",align="right",font=(markFont[0],14,markFont[2]))
t.setpos(100,180)
t.write("y=2/(x-4)",font=(markFont[0],14,markFont[2]))
t.ht()
附录4:
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t,)
#标题与函数解析式
t.setpos(0, 210)
t.write("原函数和逆函数图象",align="center",font=(markFont[0],14,markFont[2]))
#对称轴
t.setpos(-200,-200)
t.seth(45)
tmp=0
while tmp<400*2**.5+1:
t.down()
t.fd(2.5)
t.up()
t.fd(2.5)
tmp+=5
t.setpos(120,100)
t.write("y=x",font=(markFont[0],14,markFont[2]))
t.pencolor("#000088")
#y=2/(x+4)-5
def f5(x):
return 2/(x+4)-5
trace(t,-10,-4.02,f5)
trace(t,-3.98,2.02,f5)
t.setpos(-80,-180)
t.write("y=2/(x+4)-5",font=(markFont[0],14,markFont[2]))
t.setpos(40,-120)
t.write("y=2/(x+4)-5",font=(markFont[0],14,markFont[2]))
#y=2/(x+5)-4
t.pencolor("#008800")
def f6(x):
return 2/(x+5)-4
trace(t,-10,-5.02,f6)
trace(t,-4.98,1.02,f6)
t.setpos(-200,-88)
t.write("y=2/(x+5)-4",font=(markFont[0],14,markFont[2]))
t.setpos(30,-70)
t.write("y=2/(x+5)-4",font=(markFont[0],14,markFont[2]))
t.ht()
附录5:
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
build(t,)
#标题与函数解析式
t.setpos(0, 210)
t.write("原函数和逆函数图象",align="center",font=(markFont[0],14,markFont[2]))
#对称轴
t.setpos(-200,-200)
t.seth(45)
tmp=0
while tmp<400*2**.5+1:
t.down()
t.fd(2.5)
t.up()
t.fd(2.5)
tmp+=5
t.setpos(120,100)
t.write("y=x",font=(markFont[0],14,markFont[2]))
t.pencolor("#880000")
#y=-2/(x+4)+3
def f5(x):
return -2/(x+4)+3
trace(t,-10,-4.02,f5)
trace(t,-3.98,10.02,f5)
t.setpos(-200,20*f5(-10)+10)
t.write("y=-2/(x+4)+3",font=(markFont[0],14,markFont[2]))
t.setpos(200,20*f5(10)+10)
t.write("y=-2/(x+4)+3",align="right",font=(markFont[0],14,markFont[2]))
#y=-2/(x-3)-4
t.pencolor("#000088")
def f6(x):
return -2/(x-3)-4
trace(t,-10,2.98,f6)
trace(t,3.02,10.02,f6)
t.setpos(-200,20*f6(-4)+10)
t.write("y=-2/(x-3)-4",font=(markFont[0],14,markFont[2]))
t.setpos(200,20*f6(10))
t.write("y=-2/(x-3)-4",align="right", font=(markFont[0],14,markFont[2]))
t.ht()