我们知道3、4、5是一组勾股数,可以构成一个直角三角形,那三个数同时放大1倍,6、8、10还是勾股数吗?作图如下,作图代码附录1。
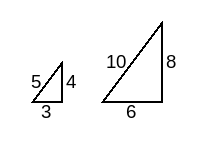
可见,同时放大边长,边长之间的比不变,三角形的内角大小也不变。直角三角形的内角与相应的边长之比保持一种一一对应的关系,我们就用锐角三角函数来表示这种对应关系。
如下图(作图代码附录2)
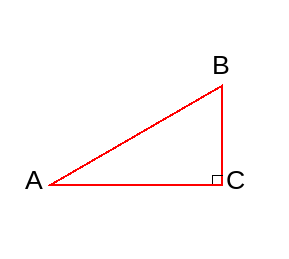
对于∠A,BC是对边,AC是邻边,加上斜边,一共有四个比
BC:AB,
AC:AB,
BC:AC,
AC:BC。
为了区分这种角度与边长之比的对应关系的不同,用四种锐角三角函数表示:
正弦函数sin∠A=BC:AB,
余弦函数cos∠A=AC:AB,
正切函数tan∠A=BC:AC,
余切函数cot∠A=AC:BC。
由于直角三角形的两个锐角的对边和邻边刚好对调,得到锐角三角函数的第一条性质——
(1)直角三角形中一个锐角的“正”函数与另一个锐角的“余”函数相等(实为恒等,变化中保持相等关系),反之亦然。
sin∠A=cos∠B,
cos∠A=sin∠B,
tan∠A=cot∠B,
cot∠A=tan∠B。
如果两个锐角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。可见直角三角形ABC中∠A与∠B互余。通过第一条性质,直接可得到锐角三角函数的第二条性质——
(2)直角三角形中一个锐角的“正”函数与一个直角减去这个锐角的差的“余”函数相等,反之亦然。
sin∠A=cos(1直角-∠A),
cos∠A=sin(1直角-∠A),
tan∠A=cot(1直角-∠A),
cot∠A=tan(1直角-∠A)。
由于
tan∠A × cot∠A = (BC:AC) × (AC:BC) = 1,
tan∠A = BC:AC = (BC/AB):(AC/AB) = sin∠A : cos∠A,
cot∠A = cos∠A : sin∠A,
得到三角函数的第三条性质——
(3)正切函数与余切函数互为倒数,正切函数是正弦函数与余弦函数的比,余切函数是余弦函数与正弦函数的比。
tan∠A × cot∠A = 1,
tan∠A = sin∠A : cos∠A,
cot∠A = cos∠A : sin∠A。
由于三角函数的实质是边的比,不失一般性,假设直角三角形ABC的斜边等于1,由勾股定理可得
BC²+AC²=1,
得到三角函数的第四条性质(重要)——
(4)正弦函数和余弦函数平方和等于1。
(sin∠A)²+(cos∠A)²=1。
例题1:如下图,已知直角三角形ABC的斜边AB是120,cot∠A=sqrt(3)(根号3),求AC和BC的长。
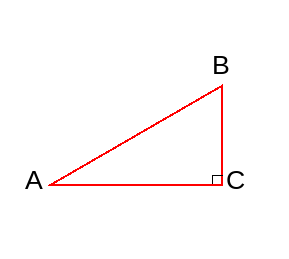
解1:有三角函数的实质是比
cot∠A = AC : BC,
(cot∠A)² = AC² : BC²,
AC² : BC² = 3,
AC²=3BC²。 ①
又由勾股定理可得
AC² + BC² = 120², ②
把①代入②,得
3BC² + BC² = 120²,
BC² = 120²/4,
BC² = 60²,
BC = 60。
把BC² = 60²代入①,得
AC²=3 × 60²,
AC = 60sqrt(3)。
即直角边AC是60sqrt(3),BC是60。
解2:由于
cot∠A = cos∠A / sin∠A,
(cot∠A)² = (cos∠A / sin∠A)²,
(cos∠A)² / (sin∠A)² = 3,
又由于
(cos∠A)² + (sin∠A)²=1
得
(sin∠A)² = 1/4,(cos∠A)²=3/4,
sin∠A = 1/2, cos∠A=sqrt(3)/2。
所以得
AC=ABcos∠A=120 × sqrt(3)/2 = 60sqrt(3),
BC=ABsin∠A=120 × 1/2 = 60。
练习题1:如下图(作图代码附录3),已知直角三角形ABC的斜边AB是30,tan∠A=3/4,参考例题1,用2种方法求AC和BC的长。

附录1:
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
t.pensize(2)
#30,40,50
t.setpos(-50, -40)
t.down()
t.setx(-20)
t.sety(0)
t.setpos(-50, -40)
t.up()
t.setpos(-35, -60)
t.write("3",align="center",font=("Arial", 14, "normal"))
t.setpos(-15, -30)
t.write("4",font=("Arial", 14, "normal"))
t.setpos(-40, -30)
t.write("5",align="right",font=("Arial", 14, "normal"))
#60,80,100
t.setpos(20, -40)
t.down()
t.setx(80)
t.sety(40)
t.setpos(20, -40)
t.up()
t.setpos(50, -60)
t.write("6",align="center",font=("Arial", 14, "normal"))
t.setpos(85, -10)
t.write("8",font=("Arial", 14, "normal"))
t.setpos(45,-10)
t.write("10",align="right",font=("Arial", 14, "normal"))
t.ht()
附录2:
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
t.pensize(2)
t.pencolor("red")
#
t.setpos(-50, -50)
t.seth(30)
t.down()
t.fd(200)
posB=t.pos()
t.seth(-90)
t.fd(100)
posC=t.pos()
t.seth(180)
t.fd(10)
pos=t.pos()
t.pensize(1)
t.pencolor("black")
t.seth(90)
t.fd(10)
t.seth(0)
t.fd(10)
t.up()
t.setpos(pos)
t.pensize(2)
t.pencolor("red")
t.down()
t.setpos(-50,-50)
t.up()
t.pencolor("black")
t.setpos(-55,-60)
t.write("A",align="right",font=("Arial", 20, "normal"))
t.setpos(posB[0],posB[1]+5)
t.write("B",align="center",font=("Arial", 20, "normal"))
t.setpos(posC[0]+5,posC[1]-10)
t.write("C",font=("Arial", 20, "normal"))
t.ht()
附录3:
import turtle as t
t.setup(500,500)
t.screensize(400,400)
t.up()
t.pensize(2)
t.pencolor("red")
#
t.setpos(-100, -100)
t.seth(0)
t.down()
t.fd(20*24)
posC=t.pos()
t.seth(90)
t.fd(20*8)
posB=t.pos()
t.setpos(-100,-100)
t.up()
t.setpos(posC[0],posC[1]+10)
t.seth(180)
t.pensize(1)
t.pencolor("black")
t.fd(10)
t.seth(-90)
t.fd(10)
t.up()
t.pensize(2)
t.pencolor("red")
t.down()
t.setpos(-100,-100)
t.up()
t.pencolor("black")
t.setpos(-105,-110)
t.write("A",align="right",font=("Arial", 20, "normal"))
t.setpos(posB[0],posB[1]+5)
t.write("B",align="center",font=("Arial", 20, "normal"))
t.setpos(posC[0]+5,posC[1]-10)
t.write("C",font=("Arial", 20, "normal"))
t.ht()