由直角三角形中的已知元素，求出其余未知元素的过程，叫做解直角三角形。直角三角形中，除直角外，共有五个元素，即三条边和两个锐角。换一种说法，就是直角三角形除直角外其它五个变量，知道其中一些变量求其它变量的值。那么知道五个元素（变量）中的几个，就可以求其余元素（变量）呢？下图直角三角形：

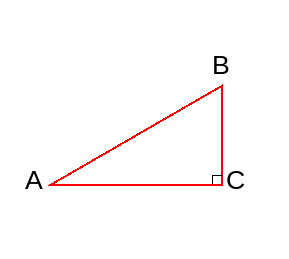
　　已知直角三角形两边，通过勾股定理

AC²+BC²=AB²

可以求第三边，有通过三角函数的逆函数（反三角函数）

arcsin(BC/AB)=∠A，

或arccos(AC/AB)=∠A

及锐角和是直角

∠A+∠B=90°

可以求出直角三角形的两个锐角。从而得到第一个可解的直角三角形

　　（１）已知二边；

另外，已知一边和一个锐角，通过三角函数

sin∠A=BC/AB，

cos∠A=AC/AB

可以求出未知的边，通过两锐角和是直角

∠A+∠B=90°

得到另外一个角，从而得到第二个可解的直角三角形

　　（２）已知一边和一锐角。

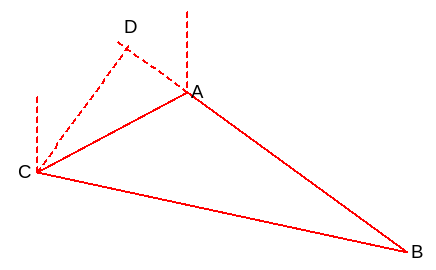
　　例题1：如下图（作图代码附录1），已知直角三角形ABC中，AC=BC=sqrt(3)，AD与BC相交与D点，DC=1，求∠BAD大小和sin∠BAD的实数值。

解：由于AC=BC，所以三角形ABC是等腰直角三角形，所以

∠BAC=45°．

又由于AC=sqrt(3)，DC=1，则

tan∠DAC=DC/AC=1/sqrt(3)

得

∠DAC=arctan(1/sqrt(3))=30°

所以

∠BAD=∠BAC-∠DAC=45°-30°=15°．

作三角形ABD底边AB上的高DE（增加的代码附录2）

由三角形EBD也是等腰直角三角形

DE = BD  / sqrt(2) =[sqrt(3)-1]  /  sqrt(2)

AD² = (sqrt(3))²+1²

AD =2

sin∠BAD=DE/AD=[sqrt(3)-1]  /  2sqrt(2)=[sqrt(6)-sqrt(2)]  /  4

　　例题1是求sin15°实数值的经典方法。

　　解直角三角形在间接测量距离和方向（或角度）有广泛的应用。

　　例题2：如下图（作图代码附录3），摄像头离地10米高，一辆车正对着摄像头开过来，第一次摄像时车对于摄像头的仰角是45°，4分之1秒后，第二次摄像时仰角是60°，问车的速度多少千米/小时（实数）？

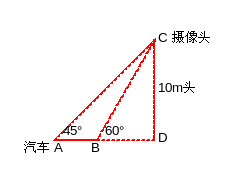
解：

AB=AD-BD，

AB=CDcot45°-CDcot60°，

AB=10[1-1/sqrt(3)]

汽车速度

V=AB/(1/4)×60×60/1000

V=10[1-1/sqrt(3)]×4×60×60/1000

V=48[3-sqrt(3)] (千米/小时)

答：车的速度48[3-sqrt(3)]千米/小时。

　　例题3：如下图（作图代码附录4），沿AC方向开山修路，为了加快施工进度，要在小山的另一边同时施工。从AC上的一点B取∠ABD=135°，BD=1km，∠D=45°．那么另一边开挖点E离D多远正好使A，C，E三点在一直线上（用实数表示结果）。

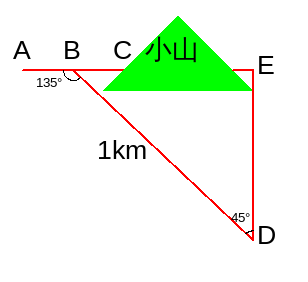
解：

∵　∠CBD=180°-∠ABD=180°-135°=45°，

∵ ∠EDB=45°，

∴　△BED是等腰直角三角形。

∴　DE=BDsin45°=1/sqrt(2)=sqrt(2)/2（km）

答：另一边开挖点E离D是sqrt(2)/2 km。

　　例题4：如下图（作图代码附录5），已知灯塔B在灯塔A正西5 n mile处，一轮船保持速度和方向不变在灯塔的南面航行，在某个时间测得距离灯塔A sqrt(113) n mile、距离灯塔B 2sqrt(17) n mile。10分钟后（未过AB线）再测量，距离灯塔A 3sqrt(17) n mile、距离灯塔B sqrt(58) n mile。求轮船的速度和方向。

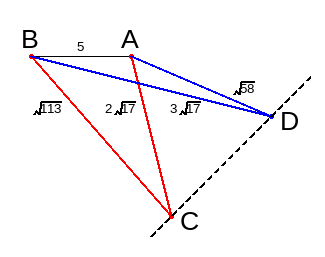
分析：要知道轮船的速度和方向，就要知道C、D点的坐标，△ABC和△ABD的三条边都确定了，这两个三角形都可以解的，但我们现在只会解直角三角形，因此把它们分为二个直角三角形，通过方程组来解。

解：以A灯塔为原点，西向东为x轴正向，南向北为y轴正向作平面直角坐标系（在代码最后顶格输入：build(t)重新运行），如下

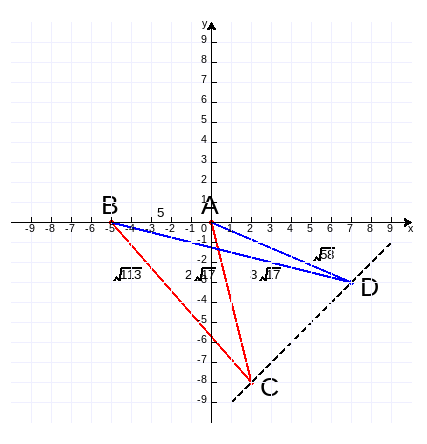
设C点坐标(x1,y1)，D点坐标(x2,y2)，则

(x1+5)²+y1²=113，　①

x1²+y1²=68，　②

(x2+5)²+y2²=153，　③

x2²+y2²=58。　④

①-②，得

5(2x1+5)=45，

x1=2，

y1=-8，（因为在第4象限）

③-④，得

5(2x2+5)=95，

x2=7，

y2=-3。（因为在第4象限）

令CD东偏北β，则

tanβ=(y2-y1)/(x2-x1)=5/5=1，

β=arctan1=45°，

CD=sqrt(5²+5²)=5sqrt(2)。

速度

V=5sqrt(2)/10×60=30sqrt(2) (n mile)。

答：轮船向东偏北45°，以30sqrt(2) n mile的速度航行。

　　上例中，使用了过二点直线的倾角计算方法

tan倾角=(y2-y1)/(x2-x1)

实际上是一次项的系数，假如，过C、D点的直线是

y=tan倾角 x + b，

y1=x1tan倾角+b，

b=y1-x1tan倾角，

b=-8-2，

b=-10。

即

y=x-10。

　　先计算倾角，再计算常数项是二点定直线的经典方法。

　　例题5：如下图（作图代码附录6），敌方导弹在20000米高空中以4马赫（4倍音速4×340m/s）来袭击，当它在离拦截点水平距离是40000米时发射导弹拦截，拦截导弹的速度为3马赫，求拦截导弹的仰角（保留小数点后2位）。

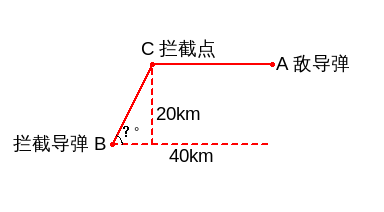
解：时间相同，速度与路程成正比，得

AC:4=BC:3。

设B到C的水平距离是x，得

(40-x):4=sqrt(x²+20²):3，

3(40-x)=4sqrt(x²+20²)，

两边平方

9*1600-720x+9x²＝16x²+16*400，

7x²+720x-5*1600=0，

取正根

x=[-720+sqrt(720²+4*7*5*1600)]/(2*7)，

x=[80sqrt(29)-360]/7。

得

tan∠B=20/x=7/[4sqrt(29)-18]，

tan∠B=7×[2sqrt(29)+9]/2/(4×29-81)，

tan∠B=[2sqrt(29)+9]/10。

得，仰角

∠B=arctan[2sqrt(29)+9]/10，

∠B≈63.16°．

答：拦截导弹的仰角约是63.16°．

　　例题6：如下图，拦水坝的横断面为梯形ABCD，AF=DE=6m．斜面坡度i=1:1.5是指坡面的铅直高度AF与水平宽度BF的比，斜面坡度i=1:3是指DE与CE的比．根据图中数据，求：

（１）坡角α和β的度数；

（２）斜坡AB的长(结果保留小数点后一位)．

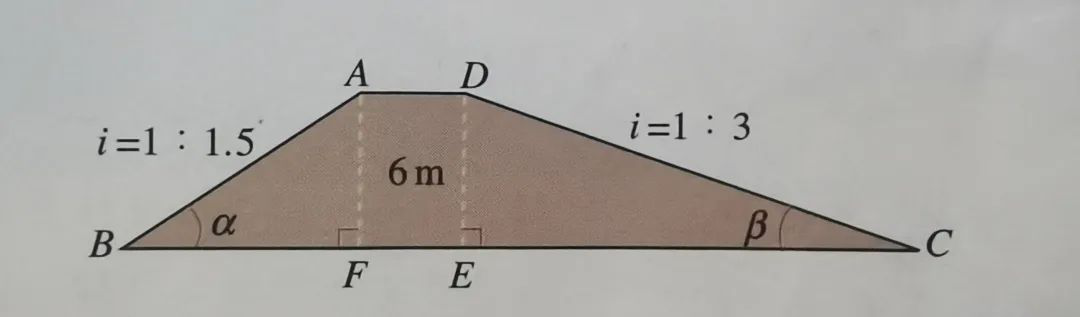
解：（１）

tanα=1/1.5，

α=arctan1/1.5，

α=33.7°．

tanβ=1/3，

β=arctan1/３，

β=18.4°．

（２）

AB=sqrt[6²+(1.5×6)²]

AB=10.8(m)．

　　例题7：如下图，海中有一个小岛A，它周围8 n mile内有暗礁．渔船跟踪鱼群由西向东航行，在B点测得小岛A在北偏东60°方向上，航行12 n mile到达D点，这时测得小岛A在北偏东30°方向上．如果渔船不改变航线继续向东航行，有没有触礁的危险？

解：作A到BD的距离，如下图（作图代码附录7）

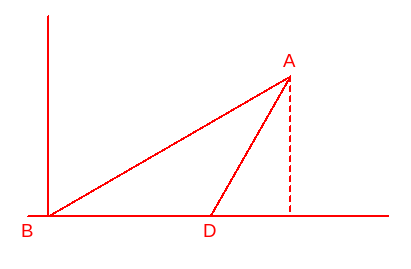
设A到BD的距离是h，则

hcot(90-60)-hcot(90-30)=12，

h=12/(cot30-cot60)，

h≈10.4 (n mile)，

h>8．

答：如果渔船不改变航线继续向东航行，没有触礁的危险．

　　例题8：多年来，很多船只、飞机都在大西洋的个区域内神秘失踪，这个区域称为百慕大三角．直至现在，人们仍未能破解这个秘密．根据下图中标出的百慕大三角的位置，计算百慕大三角的面积(结果取整数)．

　　解：延迟2720km的线，与1700km为斜边构成一个直角三角形，如下图（作图代码附录8）．

由题义可知

∠CAD=180°-(62°+54°)=64°．

△ABC面积=(1/2)AB×ACsin∠CAD=(1/2)×2720×1700sin64°

△ABC面积≈2078012km²．

即百慕大三角的面积约是2078012km²．

　　利用解直角三角形的知识解决实际问题的一般过程是：

（１）将实际问题抽象为数学问题（画出平面图形，转化为解直角三角形的问题）；

（２）根据问题中的条件，适当选用锐角三角函数等解直角三角形；

（３）得到数学问题的答案；

（４）得到实际问题的答案．

　　练习1：根据锐角三角函数的性质，设计一个计算方法，算出sin22.5°的准确实数值．

　　练习2：海中有一小岛P，在以P为圆心、半径为16√2 n mile的圆形海域内有暗礁．轮船自西向东航行，它在A处时测得小岛P位于北偏东60°方向上，且A，P之间的距离为32 n mile．若轮船继续向正东方向航行，轮船有无触礁危险？请通过计算加以说明．如果有危险，轮船自A处开始沿南偏东多少度的方向航行，能安全通过这一海域？

　　练习3：一轮船在海中航行，它前进方向的左侧有南北排列的A，B（在A的正北方）两个航标，相距1 n mile．某个时间测量，A在轮船的北偏西60°，B在轮船的北偏西30°，2分钟后再测量，A在轮船的南偏西30°，B在轮船的南偏西45°．求轮船的速度（n mile/小时）和方向（保留小数点后2位）．

　　练习4：求直线y=2x-5、y=3x+6、y=-x+7所围成的三角形面积。

　　练习5：海盗正往东北方向以每小时30 n mile逃窜，海警开始追铺时，海盗在海警的北偏西60°，距离5 n mile，海警船的速度是50 n mile，问海警船的方向是多少时最佳（保留小数点后2位）？

附录1：
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
t.pensize(2)
t.pencolor("red")
#
t.setpos(-50, -50)
t.seth(30)
t.down()
t.fd(200)
posD=t.pos()
t.seth(-90)
t.fd(100)
posC=t.pos()
t.seth(180)
t.fd(10)
pos=t.pos()
t.pensize(1)
t.pencolor("black")
t.seth(90)
t.fd(10)
t.seth(0)
t.fd(10)
t.up()
t.setpos(pos)
t.pensize(2)
t.pencolor("red")
t.down()
t.setpos(-50,-50)
t.up()
t.pencolor("black")
t.setpos(-55,-60)
t.write("A",align="right",font=("Arial", 20, "normal"))
t.setpos(posD[0]+5,posD[1]-10)
t.write("D",font=("Arial", 20, "normal"))
t.setpos(posC[0]+5,posC[1]-10)
t.write("C",font=("Arial", 20, "normal"))
t.setpos(-50,-50)
t.seth(45)
t.pencolor("red")
t.down()
t.fd(100*6**0.5)
posB=t.pos()
t.setpos(posD)
t.up()
t.setpos(posB[0]+5,posB[1]-10)
t.pencolor("black")
t.write("B",font=("Arial", 20, "normal"))
t.ht()

附录2：

t.pencolor("red")
t.setpos(posD)
t.seth(135)
h=(3**0.5-1)/2**0.5*100
for i in range(0, int(h), 5):
    t.down()
    t.fd(2.5)
    t.up()
    t.fd(2.5)
t.setpos(posD)
t.fd(h)
posE=t.pos()
t.bk(10)
t.pensize(1)
t.pencolor("black")
t.seth(45)
t.down()
t.fd(10)
t.seth(135)
t.fd(10)
t.up()
t.setpos(posE[0]-5,posE[1]+5)
t.write("E",align="center", font=("Arial", 20, "normal"))

附录3：
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
t.pensize(2)
t.pencolor("red")
#
t.setpos(-50, -50)
t.seth(45)
for i in range(0, int(100*2**0.5), 5):
    t.down()
    t.fd(2.5)
    t.up()
    t.fd(2.5)
t.setpos(50, 50)
t.dot(3)
t.seth(-90)
for i in range(0, 100, 5):
    t.down()
    t.fd(2.5)
    t.up()
    t.fd(2.5)
t.setpos(50, -50)
t.seth(180)
L2=100/3**0.5
for i in range(0, int(L2), 5):
    t.down()
    t.fd(2.5)
    t.up()
    t.fd(2.5)
t.setx(50-L2)
posL2=t.pos()
t.seth(60)
for i in range(0, int(2*L2), 5):
    t.down()
    t.fd(2.5)
    t.up()
    t.fd(2.5)
t.setpos(posL2)
t.down()
t.setx(-50)   
t.up()
t.pencolor("black")
t.setpos(-40, -48)
t.write("45°",font=("Arial", 10, "normal"))
t.setpos(posL2[0]+10, -48)
t.write("60°",font=("Arial", 10, "normal"))
t.setpos(posL2[0], -65)
t.write("B",align="center", font=("Arial", 10, "normal"))
t.setpos(-40, -65)
t.write("汽车 A",align="right", font=("Arial", 10, "normal"))
t.setpos(55, 45)
t.write("C 摄像头",font=("Arial", 10, "normal"))
t.sety(-5)
t.write("10m头",font=("Arial", 10, "normal"))
t.sety(-55)
t.write("D",font=("Arial", 10, "normal"))
t.ht()

附录3：
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
t.pensize(2)
t.pencolor("red")
#
t.setpos(-100, 100)
t.down()
t.seth(0)
t.fd(100)
t.up()
posC=t.pos()
t.seth(-135)
t.pencolor("green")
t.fillcolor("green")
t.begin_fill()
t.fd(30)
t.seth(0)
DL=30*3**0.5+100
t.fd(DL)
t.seth(135)
t.fd(30)
posE2=t.pos()
t.fd(DL/2*2**0.5-30)
t.setpos(posC)
t.end_fill()
t.up()
t.setpos(posE2)
t.down()
t.pencolor("red")
t.seth(0)
t.fd(20)
posE=t.pos()
t.seth(-90)
t.fd(170)
posD=t.pos()
t.setpos(-50, 100)
t.up()
t.pensize(1)
t.pencolor("black")
t.setpos(-60, 100)
t.down()
t.seth(-90)
t.circle(10,135)
t.up()
t.setpos(-60, 80)
t.write("135°",align="right",font=("Arial", 10, "normal"))
t.setpos(posD[0], posD[1]+10)
t.down()
t.seth(180)
t.circle(10,45)
t.up()
t.setpos(posD[0]-2, posD[1]+15)
t.write("45°",align="right",font=("Arial", 10, "normal"))
t.pencolor("black")
t.setpos(-100, 105)
t.write("A",align="center", font=("Arial", 20, "normal"))
t.setx(-50)
t.write("B",align="center", font=("Arial", 20, "normal"))
t.setx(0)
t.write("C",align="center", font=("Arial", 20, "normal"))
t.setx(50)
t.write("小山",align="center",font=("Arial", 20, "normal"))
t.setpos(posE[0]+5, 90)
t.write("E",font=("Arial", 20, "normal"))
t.sety(posD[1]-10)
t.write("D",font=("Arial", 20, "normal"))
t.setpos(25, (100+posD[1])/2-10)
t.write("1km",align="right",font=("Arial", 20, "normal"))
t.ht()

附录4：
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
t.pensize(2)
t.pencolor("red")
#
t.setpos(-100, 100)
t.down()
t.seth(0)
t.fd(100)
t.up()
posC=t.pos()
t.seth(-135)
t.pencolor("green")
t.fillcolor("green")
t.begin_fill()
t.fd(30)
t.seth(0)
DL=30*3**0.5+100
t.fd(DL)
t.seth(135)
t.fd(30)
posE2=t.pos()
t.fd(DL/2*2**0.5-30)
t.setpos(posC)
t.end_fill()
t.up()
t.setpos(posE2)
t.down()
t.pencolor("red")
t.seth(0)
t.fd(20)
posE=t.pos()
t.seth(-90)
t.fd(170)
posD=t.pos()
t.setpos(-50, 100)
t.up()
t.pensize(1)
t.pencolor("black")
t.setpos(-60, 100)
t.down()
t.seth(-90)
t.circle(10,135)
t.up()
t.setpos(-60, 80)
t.write("135°",align="right",font=("Arial", 10, "normal"))
t.setpos(posD[0], posD[1]+10)
t.down()
t.seth(180)
t.circle(10,45)
t.up()
t.setpos(posD[0]-2, posD[1]+15)
t.write("45°",align="right",font=("Arial", 10, "normal"))
t.pencolor("black")
t.setpos(-100, 105)
t.write("A",align="center", font=("Arial", 20, "normal"))
t.setx(-50)
t.write("B",align="center", font=("Arial", 20, "normal"))
t.setx(0)
t.write("C",align="center", font=("Arial", 20, "normal"))
t.setx(50)
t.write("小山",align="center",font=("Arial", 20, "normal"))
t.setpos(posE[0]+5, 90)
t.write("E",font=("Arial", 20, "normal"))
t.sety(posD[1]-10)
t.write("D",font=("Arial", 20, "normal"))
t.setpos(25, (100+posD[1])/2-10)
t.write("1km",align="right",font=("Arial", 20, "normal"))
t.ht()

附录5：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
import turtle as t
from fractions import Fraction
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t,draw=False)  #,draw=False
#B
circularDot(t, -5, 0,  "red", size=5)
line(t,-5,0,0,0)
circularDot(t, 0, 0,  "red", size=5)

t.pensize(2)
t.pencolor("red")
line(t,-5,0,2,-8)
line(t,0,0,2,-8)
circularDot(t, 2, -8,  "red", size=5)

t.pencolor("blue")
line(t,-5,0,7,-3)
line(t,0,0,7,-3)
circularDot(t, 7, -3,  "blue", size=5)
t.pencolor("black")
t.setpos(20,-9*20)
t.seth(45)
for i in range(0,int(160*2**0.5), 10):
    t.down()
    t.fd(5)
    t.up()
    t.fd(5)
    
t.setpos(-5*20, 2)
t.write("B",align="center",font=("Arial", 20, "normal"))
t.setx(-2.5*20)
t.write("a",align="center",font=("Arial", 10, "normal"))
t.setx(0)
t.write("A",align="center",font=("Arial", 20, "normal"))
t.setpos(2*20+10,-8*20-20)
t.write("C",font=("Arial", 20, "normal"))
t.setpos(7*20+10,-3*20-20)
t.write("D",font=("Arial", 20, "normal"))
t.setpos(-3*20,-3*20)
t.write("b1",align="right",font=("Arial", 10, "normal"))
t.setx(-2)
t.write("c1",font=("Arial", 10, "normal"))
t.setx(4*20)
t.write("b2",align="right",font=("Arial", 10, "normal"))
t.setpos(5*20,-2*20)
t.write("c2",align="right",font=("Arial", 10, "normal"))
t.ht()

附录6：

import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from mymath.rooting import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t,draw=False)  #,draw=False
t.pensize(2)
t.pencolor("red")
#
circularDot(t, 4, 2,  "red", size=5)
line(t,4,2,-2,2)
circularDot(t, -2, 2,  "red", size=5)
line(t,-2,2,-4,-2)
circularDot(t, -4, -2,  "red", size=5)
t.setpos(-4*20, -2*20)
t.seth(0)
for i in range(0,8*20, 10):
    t.down()
    t.fd(5)
    t.up()
    t.fd(5)
t.setx(-2*20)
t.seth(90)
for i in range(0,4*20, 10):
    t.down()
    t.fd(5)
    t.up()
    t.fd(5)
t.pencolor("black")   
t.pensize(1)
t.setpos(-4*20+10, -2*20)
t.seth(90)
t.down()
t.circle(10,atan2(2,1)*180/pi)
t.up()
t.setpos(4*20+5, 2*20-10)
t.write("A 敌导弹",font=("Arial", 14, "normal"))
t.setpos(-2*20-10, 2*20+5)
t.write("C 拦截点", font=("Arial", 14, "normal"))
t.setpos(-4*20-5, -2*20-10)
t.write("拦截导弹 B",align="right",font=("Arial", 14, "normal"))
t.setpos(0,-2*20-22)
t.write("40km",align="center",font=("Arial", 14, "normal"))
t.setpos(-2*20+5,0-20)
t.write("20km",font=("Arial", 14, "normal"))
t.setpos(-4*20+10,-2*20+5)
t.write("？°",font=("Arial", 10, "normal"))
t.ht()

附录7：

import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
t.pensize(2)
t.pencolor("red")
#
t.setpos(-180,-100)
t.down()
t.setx(180)
t.up()
t.setx(-160)
t.down()
t.sety(100)
t.up()
t.sety(-100)
t.seth(30)
t.down()
t.fd(280)
posA=t.pos()
t.seth(-120)
t.fd(2*7/3**0.5*20)
posD=t.pos()
t.up()
t.setpos(posA)
t.seth(-90)
for i in range(0,140,10):
    t.down()
    t.fd(5)
    t.up()
    t.fd(5)
t.setpos(-180, -125)
t.write("B", align="center", font=("Arial", 14, "normal"))
t.setpos(posD[0],posD[1]-25)
t.write("D", align="center", font=("Arial", 14, "normal"))
t.setpos(posA[0], posA[1]+5)
t.write("A",align="center",font=("Arial", 14, "normal"))
t.ht()

附录8：

from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
t.pensize(2)
t.pencolor("red")
#
t.setpos(-100,180)
t.seth(-90)
for i in range(0,80,10):
    t.down()
    t.fd(5)
    t.up()
    t.fd(5)
posA=(-100,100)
t.setpos(posA)
t.seth(-36)
for i in range(0,90,10):
    t.down()
    t.bk(5)
    t.up()
    t.bk(5)
t.setpos(posA)    
t.down()
t.fd(272)
t.up()
posB=t.pos()
t.setpos(posA)    
t.seth(-152)
t.down()
t.fd(170)
posC=t.pos()
t.setpos(posB)
t.up()
t.setpos(posC)
t.seth(54)
for i in range(0,int(170*sin(64*pi/180)),10):
    t.down()
    t.fd(5)
    t.up()
    t.fd(5)
posD=t.pos()
t.setpos(posC)
t.seth(90)
for i in range(0,80,10):
    t.down()
    t.fd(5)
    t.up()
    t.fd(5)
t.pencolor("black")
t.setpos(posA[0]+5, posA[1]-10)
t.write("A", font=("Arial", 14, "normal"))
t.setpos(posB[0]+5,posB[1]-10)
t.write("B",  font=("Arial", 14, "normal"))
t.setpos(posC[0]-5, posC[1]-10)
t.write("C",align="right",font=("Arial", 14, "normal"))
t.setpos(posD[0], posD[1]+5)
t.write("D",align="center",font=("Arial", 14, "normal"))
t.ht()