下图是直角坐标系中的一个圆（作图代码附录1）

不难发现，在-5<x<5的范围内，每个x值都有2个y值与它对应．从函数的定义可知，在平面直角坐标系中是不能用函数表示这个圆的．

　　为了能用函数来研究圆和类似圆的图形，就不能使用直角坐标系了．于是极坐标系就流行开来．

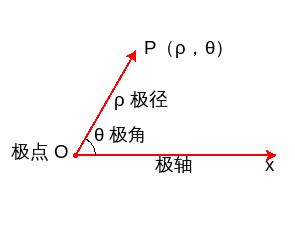
　　极坐标系（polar coordinates）是指在平面内由极点、极轴和极径组成的坐标系。在平面上取定一点O，称为极点。从O出发引一条射线Ox，称为极轴。再取定一个单位长度，通常规定角度取逆时针方向为正。这样，平面上任一点P的位置就可以用线段OP的长度ρ以及从Ox到OP的角度θ来确定，有序数对（ρ，θ）就称为P点的极坐标，记为P（ρ，θ）；ρ称为P点的极径，ρ≥0，θ称为P点的极角。下图是极坐标系示意图（作图代码附录2）．

　　极坐标系中P点的两个坐标ρ和θ可以由下面的公式转换为直角坐标系下的坐标值：

x=ρcosθ，

y=ρsinθ．

　　有了极坐标系，我们就可以探索极坐标下的函数了．

　　我们知道，一个直角坐标系下的0次函数，例如，y=5是过(0,5)点平行于x轴的直线；那在极坐标系下的0次函数，例如，ρ=5会是什么样子呢？下图（作图代码附录3）．

　　可见，极坐标系下的0次函数是半径为这个常数的圆（作为极径的常数要大于0）．用函数表示圆就迎刃而解了．

　　我们也知道，一个直角坐标系下的正比例函数，例如，y=x或y=-x是过原点(0,0)点的一条直线；那在极坐标系下的正比例函数，例如，ρ=θ（θ≥０）和ρ=-θ（θ≤０）会是什么样子呢？下2图（作图代码附录4，5）．

　　可见，极坐标系下的正比例函数是阿基米德螺线，比例系数符号改变螺线的旋转方向（正，逆时针，负，顺时针）．

　　把ρ=θ（θ≥０）和ρ=-θ（θ≤０）的图象画在一起如下（作图代码附录6）．

　　可见，ρ=θ（θ≥０）和ρ=-θ（θ≤０）的图象轴对称，对称轴是极轴所在的直线．

　　极坐标系下的正比例函数的比例不等于1或-1的情况，例如ρ=(1/2)θ．图象如下（作图代码附录7）．

　　可见，比例系数（一次项系数）的绝对值大小改变阿基米德螺线的螺距．

　　极坐标系下一般的一元一次函数，即阿基米德螺线方程ρ=a+bθ，例如ρ=1+θ(θ≥-1)和ρ=-1+θ(θ≥1)的图象如下（作图代码附录8，9）．

　　可见，常数项只改变螺线的＂相位＂（从极点出发时的方向）．

　　根据上面的性质，如果常数项相差2π，那么函数的曲线重叠．为此，在上面的图象上画ρ=-1+2π+θ(θ≥1-2π)的图象，直接在idle中添加代码（附录10）．

　　例题1：制作一张由相位不一样的五条阿基米德螺线组成的旋风图．

作图：如下，作图代码附录11．

　　练习题1：通过修改例题1的代码，制作一张由六条阿基米德螺线组成的旋风图．

附录1：

import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
build(t)
t.pensize(2)
t.setpos(0,210)
t.write("平面直角坐标系中的圆",align="center", font=("Arial", 14, "normal"))   
t.setpos(100,0)
t.seth(90)
t.down()
t.circle(100)
t.up()
t.ht()

附录2：
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
t.setpos(0,210)
t.write("极坐标系中示意图",align="center", font=("Arial", 14, "normal"))   
t.pensize(2)
t.pencolor("red")
t.fillcolor("red")
#极点
t.setpos(0,0)
t.dot(5)
#极轴
t.seth(0)
t.down()
t.fd(200)
t.stamp()
t.up()
#极径
t.setpos(0,0)
t.seth(60)
t.down()
t.fd(120)
t.stamp()
t.up()
posP=t.pos()
t.setpos(20,0)
t.seth(90)
t.down()
t.pensize(1)
t.pencolor("black")
t.circle(20,60)
t.up()
t.setpos(-5,-7)
t.write("极点 O",align="right", font=("Arial", 14, "normal"))   
t.setpos(200,-20)
t.write("x",align="right", font=("Arial", 14, "normal"))   
t.setx(100)
t.write("极轴",align="center", font=("Arial", 14, "normal"))   
t.setpos(posP[0]+10,posP[1]-7)
t.write("P（ρ，θ）",font=("Arial", 14, "normal"))   
t.seth(-120)
t.fd(60)
t.write("ρ 极径",font=("Arial", 14, "normal"))  
t.fd(40)
t.write("θ 极角",font=("Arial", 14, "normal"))  
t.ht()

附录3：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
from fractions import Fraction
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
build(t)
t.up()
t.setpos(0,210)
t.write("极坐标系中ρ=5函数图象",align="center", font=("Arial", 14, "normal"))  
#画极轴
t.pensize(2)
t.pencolor("red")
t.fillcolor("red")
t.setpos(-5,5)
t.write("O",align="right", font=("Arial", 14, "normal"))   
t.setpos(0,0)
t.dot(5)
t.seth(0)
t.down()
t.fd(200)
t.stamp()
t.up()
#极坐标0次函数
S=20  #默认放大比例与build(t)对应
R=5*S #ρ=5
t.speed(0)  #最大速度
#x正向射线为极轴
def draw(x):
    _t=x*pi/180  #弧度
    t.setpos(R*cos(_t),R*sin(_t))  #极坐标转直角坐标
t.setpos(R,0) #把画笔置于开始点
t.down()
for i in range(0,361):
    for j in range(S):
        draw(i+Fraction(j, S))
t.up()
t.ht()

附录4：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
from fractions import Fraction
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
build(t,xUnt=(1,10),yUnt=(1,10))
t.up()
t.setpos(0,210)
t.write("极坐标系中ρ=θ函数图象",align="center", font=("Arial", 14, "normal"))  
#画极轴
t.pensize(2)
t.pencolor("red")
t.fillcolor("red")
t.setpos(-5,-25)
t.write("O",align="right", font=("Arial", 14, "normal"))   
t.setpos(0,0)
t.dot(5)
t.seth(0)
t.down()
t.fd(200)
t.stamp()
t.up()
#极坐标1次函数
S=10  #默认放大比例与build(t)对应
t.speed(0)  #最大速度
#x正向射线为极轴
def draw(x):  #x是弧度
    t.setpos(S*x*cos(x),S*x*sin(x))  #极坐标转直角坐标
t.setpos(0,0) #把画笔置于开始点
t.down()
for i in range(0,1081):
    for j in range(S):
        draw((i+Fraction(j, S))*pi/180)
t.up()
t.ht()

附录5：

import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
from fractions import Fraction
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
build(t,xUnt=(1,10),yUnt=(1,10))
t.up()
t.setpos(0,210)
t.write("极坐标系中ρ=-θ函数图象",align="center", font=("Arial", 14, "normal")) 
#画极轴
t.pensize(2)
t.pencolor("red")
t.fillcolor("red")
t.setpos(-5,5)
t.write("O",align="right", font=("Arial", 14, "normal"))   
t.setpos(0,0)
t.dot(5)
t.seth(0)
t.down()
t.fd(200)
t.stamp()
t.up()
#极坐标1次函数
S=10  #默认放大比例与build(t)对应
t.speed(0)  #最大速度
#x正向射线为极轴
def draw(x):  #x是弧度
    _r=S*(-x)  #因为x≤0
    t.setpos(_r*cos(x), _r*sin(x))  #极坐标转直角坐标
t.setpos(0,0) #把画笔置于开始点
t.down()
for i in range(0,-1081,-1):
    for j in range(0,-S,-1):
        draw((i+Fraction(j, S))*pi/180)
t.up()
t.ht()

附录6：

import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
from fractions import Fraction
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
build(t,xUnt=(1,10),yUnt=(1,10))
t.up()
t.setpos(0,210)
t.write("极坐标系中ρ=θ和ρ=-θ函数图象",align="center", font=("Arial", 14, "normal"))   

#画极轴
t.pensize(2)
t.pencolor("red")
t.fillcolor("red")
t.setpos(-5,5)
t.write("O",align="right", font=("Arial", 14, "normal"))   
t.setpos(0,0)
t.dot(5)
t.seth(0)
t.down()
t.fd(200)
t.stamp()
t.up()
#极坐标1次函数
S=10  #默认放大比例与build(t)对应
t.speed(0)  #最大速度
#x正向射线为极轴
stp=1 #符号
def _draw(x):  #x是弧度
    _r=S*x*stp
    t.setpos(_r*cos(x), _r*sin(x))  #极坐标转直角坐标
def draw():
    for i in range(0,1081*stp,stp):
         for j in range(0,S*stp,stp):
            _draw((i+Fraction(j, S))*pi/180)    
t.setpos(0,0) #把画笔置于开始点
t.down()
t.pencolor("green")
t.fillcolor("green")
draw()
t.up()
t.setpos(0,0)
t.down()
stp=-1
t.pencolor("blue")
t.fillcolor("blue")
draw()
t.up()
t.ht()

附录7：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
from fractions import Fraction
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
build(t,xUnt=(1,10),yUnt=(1,10))
t.up()
t.setpos(0,210)
t.write("极坐标系中ρ=(1/2)θ函数图象",align="center", font=("Arial", 14, "normal"))   

#画极轴
t.pensize(2)
t.pencolor("red")
t.fillcolor("red")
t.setpos(-5,5)
t.write("O",align="right", font=("Arial", 14, "normal"))   
t.setpos(0,0)
t.dot(5)
t.seth(0)
t.down()
t.fd(200)
t.stamp()
t.up()
#极坐标1次函数
S=10  #默认放大比例与build(t)对应
t.speed(0)  #最大速度
#x正向射线为极轴
stp=1 #符号
b=Fraction(1,2) #比例系数，一次项系数
def _draw(x):  #x是弧度
    _r=S*x*stp*b
    t.setpos(_r*cos(x), _r*sin(x))  #极坐标转直角坐标
def draw():
    for i in range(0,1081*stp,stp):
         for j in range(0,S*stp,stp):
            _draw((i+Fraction(j, S))*pi/180)    
t.setpos(0,0) #把画笔置于开始点
t.down()
t.pencolor("blue")
draw()
t.up()
t.ht()

附录8：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
from fractions import Fraction
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
build(t,xUnt=(1,10),yUnt=(1,10))
t.up()
t.setpos(0,210)
t.write("极坐标系中ρ=1+θ(θ≥-1)函数图象",align="center", font=("Arial", 14, "normal"))   
#画极轴
t.pensize(2)
t.pencolor("red")
t.fillcolor("red")
t.setpos(-5,5)
t.write("O",align="right", font=("Arial", 14, "normal"))   
t.setpos(0,0)
t.dot(5)
t.seth(0)
t.down()
t.fd(200)
t.stamp()
t.up()
#极坐标1次函数
S=10  #默认放大比例与build(t)对应
t.speed(0)  #最大速度
#x正向射线为极轴
stp=1 #符号
b=1 #比例系数，一次项系数
a=1 #常数项
def _draw(x):  #x是弧度
    _r=S*(a+x*stp*b)
    t.setpos(_r*cos(x), _r*sin(x))  #极坐标转直角坐标
def draw():
    _start=-a/b
    for i in range(0,1081*stp,stp):
         for j in range(0,S*stp,stp):
            _draw(_start+(i+Fraction(j, S))*pi/180)    
t.setpos(0,0) #把画笔置于开始点
t.down()
t.pencolor("blue")
draw()
t.up()
t.ht()

附录9：
import sys
sys.path.append("/5xstar/pyfiles")
from mymath.rcs import *
from math import *
from fractions import Fraction
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
build(t,xUnt=(1,10),yUnt=(1,10))
t.up()
t.setpos(0,210)
t.write("极坐标系中ρ=-1+θ(θ≥1)函数图象",align="center", font=("Arial", 14, "normal"))   
#画极轴
t.pensize(2)
t.pencolor("red")
t.fillcolor("red")
t.setpos(-5,5)
t.write("O",align="right", font=("Arial", 14, "normal"))   
t.setpos(0,0)
t.dot(5)
t.seth(0)
t.down()
t.fd(200)
t.stamp()
t.up()
#极坐标1次函数
S=10  #默认放大比例与build(t)对应
t.speed(0)  #最大速度
#x正向射线为极轴
stp=1 #符号
b=1 #比例系数，一次项系数
a=-1 #常数项
def _draw(x):  #x是弧度
    _r=S*(a+x*stp*b)
    t.setpos(_r*cos(x), _r*sin(x))  #极坐标转直角坐标
def draw():
    _start=-a/b
    for i in range(0,1081*stp,stp):
         for j in range(0,S*stp,stp):
            _draw(_start+(i+Fraction(j, S))*pi/180)    
t.setpos(0,0) #把画笔置于开始点
t.down()
t.pencolor("green")
draw()
t.up()
t.ht()

附录10：
>>> a+=2*pi
>>> t.setpos(0,0)
>>> t.down()
>>> t.pencolor("blue")
>>> t.fillcolor("blue")
>>> t.st()
>>> draw()

附录11：
from math import *
from fractions import Fraction
import turtle as t
t.setup(500,500)
t.screensize(400,400)  
t.up()
t.setpos(0,210)
t.write("五线旋风图",align="center", font=("Arial", 14, "normal"))   
#极坐标1次函数
S=10  #1对应的像素数
t.speed(0)  #最大速度
stp=1 #符号
b=1 #比例系数，一次项系数
a=0 #常数项
def _draw(x):  #x是弧度
    _r=S*(a+x*stp*b)
    t.setpos(_r*cos(x), _r*sin(x))  #极坐标转直角坐标
def draw():
    _start=-a/b
    for i in range(0,1081*stp,stp):
         for j in range(0,S*stp,stp):
            _draw(_start+(i+Fraction(j, S))*pi/180)  
_step=2*pi/5
t.pensize(4)
for i in range(5):  
    t.setpos(0,0) #把画笔置于开始点
    t.down()
    if i==0:
        t.pencolor("#AA0000")
    elif i==1:
        t.pencolor("#AAAA00")
    elif i==2:
        t.pencolor("#00AA00")
    elif i==3:
        t.pencolor("#00AAAA")
    elif i==4:
        t.pencolor("#0000AA")
    draw()
    t.up()
    a+=_step
t.ht()