公元前3000年左右巴比伦和埃及的数学出现前所未有的发展，普遍认为这两个地方是现代数学的鼻祖——古典希腊数学（里程碑著作：欧几里得《原本》）的萌芽地。

　　巴比伦人首先对数学主干作出了贡献。

　　巴比伦人采用一种楔形的数的记号，如下图

。巴比伦数系的特点是以60为进位制，并采用进位符号。在巴比伦记数制中，代表1和10的2个记号是基本记号。从1到59这些数都是由这2个基本记号结合而成的。

　　这种数的记号使加减法只是加上或去掉这种记号。整数的乘法，比方说，乘以37，拆分为乘30的积与乘7的积的和。利用倒数来做整数除法，他们把倒数化成60进制的“小数”，采用一种倒数表进行计算。这种以60的幂为分母的分数写法，在2000多年后仍被希腊数学家希帕恰斯(Hipparchus)和托勒密(Claudius Ptolemy)所采用，并且在欧洲一直沿用到16世纪文艺复兴时期，之后才被以10为底的10进制小数所代替。

　　巴比伦人也有表示平方、平方根、立方和立方根的数表。当方根是整数时是准确值，否则是近视值。例如，他们给出的2的平方根近似值是1.414213…而不是1.414214…。没有证据说明他们认识到有些方根是无理数。

　　巴比伦人已知道二次方程根的公式，解多达10个未知数的线性方程。他们还能用数表解决三次根和指数函数值(复利问题)。在一些具体问题中，出现算术数列和几何数列和的计算。

　　更加可贵的是，巴比伦代数中出现了数论（被认为是纯数学）的萌芽。他们很可能用下面正确方法，

若x=p²-q²，

y=2pq，

z=p²+q²,

则x²+y²=z²，

求出了好几组勾股数(毕达哥拉斯三元数组)。另外，还求出了

x²+y²=2z²

的整数解。

　　遗憾的是，巴比伦人不重视几何，几何也不是他们一门独立的学科。几何的发展停留在土地测量、工程所需砖数等实际问题上，这类问题很易于化为代数问题。不过，他们应该知道直角三角形的勾股定理（毕达哥拉斯定理）关系，及相似三角形的比例关系的。他们似用

A=c²/12(其中c表示圆的周长)

这个近似方法（相当于π=3）得出圆的面积。然而，在求正六边形及其外接圆周长之比时，使用π=3.125来计算。这些说明他们不一定知道π这个数。总之，巴比伦人的几何内容只是收集了一些计算简单平面图形面积和简单立体体积的法则，并不专为几何而研究几何，总是为解决实际问题时才去研究几何的。

　　现在来说古埃及了。古埃及人造出了他们自己的几套文字。其中有一套是象形文字,每个文字记号是某件东西的图形。数的部分记号如下

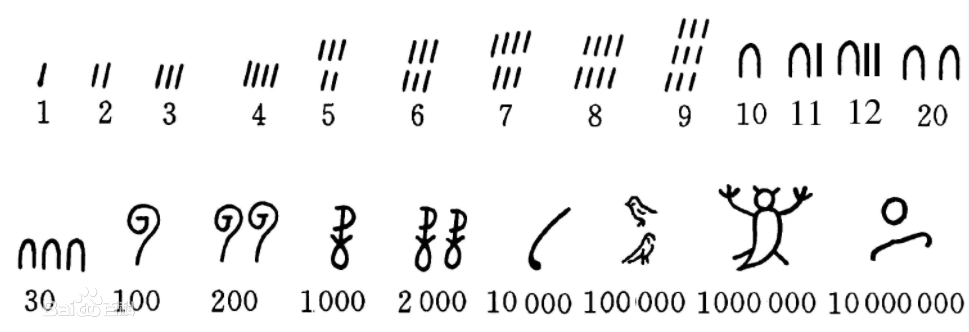
。另一套是拼音文字僧侣文( hieratic writing)，数的部分记号如下

。古埃及的数是没有进位制的，分数也使用单位分数之和来表示。

　　他们的算术主要用叠加法。做通常加减法时，他们只是靠添上或划掉一些记号，以求得最后结果。

　　乘除法也是化成叠加步骤来做的。比如说，计算

12×15

时，埃及人的用得较多的做法：首先以一个操作数开始，列出倍增表

1　　　　15

2　　　　30

4　　　　60

8　　　　120

，然后从倍增数列总选出一些数

8、4，

使它们的和等于另一个操作数

8+4=12，

它们对应值的和

120+60=180，

就是原式的积。

　　乘10的算法他们也会做，这时他们把表示1的记号改成表示10的记号，把表示10的记号改成表示100的记号，如此类推。

　　古埃及人的整数除法和整数乘法差不多，商的整数部分用倍增表，余数部分用倍减表。例如，他们做

99÷16

时，首先从16开始做出倍增表

1　　　　16

2　　　　32

4　　　　64

，得到商的整数部分是

4+2=6，

余数是

99-(64+32)=3。

接着做倍分表

1/2　　　　8

1/4　　　　4

1/8　　　　２

1/16　　　　1

，由于

2+1=3，

所以原式商的分数部分是

1/8+1/16，

与整数部分合并是

6+1/8+1/16。

　　虽然古埃及数系中没有进位，但通过观察上面乘除法的过程，貌似它们掌握二进制数的性质。这个与中国《易经》中的二进制数似乎同出一辙。直到现在中国还有一些地方使用十六两称，“半斤八两”这个成语几乎人人皆知，这些说明中国人的数学思维中也有深刻的二进制烙印。至于中国人数学思维中二进制与古埃及人数学思维中二进制有无关系，就不得而知了。

　　古埃及数系中分数的记法比我们今日的复杂得多。一些分数的象形文字写法如下

。除了几个特殊分数之外，所有分数都拆成单位分数（分子是1的分数）。例如，7/29的表达式是

。至于为什么要拆成单位分数，估计是为了能进行分数的四则运算。古埃及人之所以未能把算术和代数发展到高的水平，其分数运算之繁复也是原因之一。

　　古埃及算术里也如古巴比伦一样未能认识到无理数的性质。代数问题中出现的简单平方根，他们是用整数和分数来表达的。

　　古埃及可以解决用一元一次方程的问题，但没有形成一门独特的学科——解方程。还有就是如

ax²=b

的简单一元二次方程问题。

　　从具体问题的解决中可以看到，古埃及人掌握算术数列和几何数列的一般规律。

　　古埃及人也像古巴比伦人那样，把几何看作实用工具，主要用来解有关面积、体积及其他几何性质的问题。根据历史学家的论说，古埃及尼罗河每年泛滥后需要重新丈量土地。古埃及人有计算矩形和梯形面积的固定方法。用一个数乘另一个数的一半作为三角形面积，但我们不能确定是2条边还是一边和这边上的高。圆的面积

A=(8d/9)²，其中d是直径，

这就等于取π=3.1605，对于那个时代，是非常“准确”了。

　　古埃及人也有算立方体、箱体、柱体和其他图形体积的算法。有些算法是对的，有些只是近似。例如，圆台的体积

这里h是高，(D+d)/2是平均周长。这个公式相当于取π为3。

　　古埃及几何里最了不起的是计算正棱台（底是正方形）的正确体积公式

了，其中h是高，a和b是上下底的边。

　　传说古埃及的拉绳人(土地测量员)在绳上打结，把全长分成长度各为3比4比5的三段，然后用来形成直角三角形之说，不过未能从现有的史料中得到证实。也就是说，古埃及人可能已经了解勾股数（3、4、5）的知识。

　　我们生活的世界处处存在着关于数量和空间的问题，数学中以空间形式（简称形）为研究对象的分支，叫做几何学。

　　相传，我国在夏禹治水时期就已有规、矩、准、绳等测量工具。约公元前11世纪的西周初期，人们已经知道勾股数（3、4、5）的知识了。至于这个知识是否来源于巴比伦或古埃及就不得而知了。

　　大量事实说明，人类的测量活动是几何学形成的直接原因。以至于，几何学的英文单词geometry就是由geo(土地)和metry(测量)组成的。

参考资料：

《古今数学思想》【美】莫里斯·克莱因