上一节已经说过现代数学的鼻祖是古典希腊数学，那具体在什么时间诞生的？为什么会诞生？

　　约公元前7世纪，第一，希腊人把他们用过的各种象形文字书写系统改换成腓尼基人的拼音字母，提高了书写效率；第二，广泛使用草片做为书写介质，大大降低了书写成本，促进文化活动繁荣和思想的传播；第三，航海技术发达，可到地中海亚非欧沿海地区，与地中海其它地区（特别是巴比伦和埃及）的文化深入交流成为可能；第四，农业生产技术的进步和海洋经济的兴起，可以养活更多的“闲人”；第五，人们把“无用”的数学（纯粹数学）作为最高的艺术以追求，崇拜那些数学家、哲学家、科学家，而不是我们今天的有权人、有钱人、明星。

　　古代希腊文明虽然一直延续到公元600年，但从数学史的角度来看分两个阶段：公元前600年到前300年的古典时期；公元前300年到公元600年的亚历山大时期(或称希腊时期)。

　　古希腊人结束游牧，定居发展农业，得益于生产力的提高和海洋经济的发达，一部分人（主要是贵族）从物质生产活动中解放出来。这些人，许多到埃及游历和学习，以至于，许多古典希腊著述中提及埃及人的学问，会错误地认为埃及人是科学(特别是测量、天文学和算术)的创始者。有一些则去巴比伦学习数学和科学。

　　小亚细亚爱奥尼亚(Ionia)地区的一个城市米利都(Miletus)

是希腊哲学、数学和科学的诞生地。米利都是濒临地中海的一个富庶商业大城。来自希腊本土、腓尼基和埃及的船舶都驶进它的港口；往东有通商大道与巴比伦相通。公元前540年左右，爱奥尼亚地区波斯侵占，但仍允许米利都保持一定独立性，还能保持它在文化上的重要地位。公元前494年，爱奥尼亚地区人反抗波斯的统治失败后，爱奥尼亚在文化上的重要地位就开始衰落了。公元前479年，希腊击败波斯，重获爱奥尼亚领土，但此后文化活动地区便移到希腊本土，雅典成为其活动中心。

　　古典希腊数学先后在几个中心发展起来的，每一中心都是在前人工作的基础上添筑。一群学者在一两个大学者领导下开展活动，这样的组织就是古典时期的“学派”。这类组织与现代大学里的项目组有点相似，但组织的目标往往大相庭径。在组织的目标上，“学派”更像一个俱乐部，专给一些爱好哲学、数学和科学（这三样东西在当时物质生产活动中没多大作用）的“闲人”追求一种高尚的“艺术”。这个类似于中国古代东汉末年、三国、南北朝时的“清谈”帮，例如“竹林七贤”。

　　第一个学派是爱奥尼亚（Ionian）学派，是米利都的泰勒斯（Thales，约公元前640——约前546）创立的。哲学家阿那克西曼德（Anaximander，约公元前610——约前547）和阿那克西米尼（Anaximenes，约公元前550——前480）是他的学生，阿那克萨哥拉（Anaxagoras，约公元前500——约前428）也属于这学派的。据说泰勒斯预报了公元前585年的一次日食，又据说他根据相似三角形的性质，用一根已知长度的竹子通过测量金字塔的高度，测量船舶到海岸的距离。

　　毕达哥拉斯（Pythagoras，约公元前585——约前500）生于靠近小亚细亚海岸的萨摩斯岛（Samos）。据说他在米利都跟泰勒斯学了一段时间数学后，到各地（包括埃及和巴比伦）游历。在游历期间，不但可能除了学到一些数学知识外，还学到了一些神秘主义的教条。然后他定居在克罗顿（Croton）成立了自己的学派——毕达哥拉斯学派。毕达哥拉斯学派与其他学派的一个不同点是他们参与政治活动。他们同贵族党派结盟，因而在民主党派得势时被驱逐。约公元前497年，毕达哥拉斯逃奔到邻近的米太旁登（Metapontum）时被害。之后，他的门人散居到希腊其他学术中心，继续传授他的学说。

　　毕达哥拉斯学派与别的学派相比，还有一个显著的不同点，它是一个宗教、科学和哲学性质的帮会，有严密的组织，会员人数也是限定的，并由领导人传授知识，对于所传授的知识要保密。不过，有人认为对于数学和物理知识，他们无需保密。

　　毕达哥拉斯学派的学者们没有书面著作传世，这些人的学说是通过他人（如柏拉图和希罗多德（Herodotus））的著作间接得到的。我们把公元前585年到公元前400年毕达哥拉斯及其门徒所取得的成就归功于毕达哥拉斯是为了方便起见。菲洛劳斯（Philolaus，公元前5世纪）和阿基塔斯（公元前428——前347）是这个学派中的杰出代表。

　　古典希腊数学无疑是继承了巴比伦和埃及数学，但却产生了质的飞跃。其中一个重大贡献是数学概念抽象化——数学上的东西如数和图形是思维的抽象，同实际事物或实际形象是截然不同的。有些原始文明社会（例如埃及和巴比伦)的人诚然也知道把数脱离实物来思考，但他们可能是不自觉的。而且在希腊人之前的所有文明中，几何思想肯定是离不开实物的。例如，埃及人的直线就无非是拉紧的绳或田地的一边，而矩形则是田地的边界。

　　数学概念抽象化归功于毕达哥拉斯学派。不过在早期，他们把数看作是真实物质对象的终极组成部分，数不能离开感觉到的对象而独立存在（阿里士多德论断）。或者说，万物由（整）数组成；又或者说，数乃宇宙的唯一原素。这个时期，他们心目中的数就如同我们心目中的原子一样。

　　也许，公元前6世纪到前5世纪的毕达哥拉斯学派并没有把数和几何上的点区分开来。因此他们从几何角度把一个数看作是扩大了的一个点或很小的个球。但根据普罗克洛斯的记述，欧德摩斯说：与埃及人和巴比伦人相比，毕达哥拉斯认识到较高级的数学原理，并且能纯凭心智来考虑抽象问题。欧德摩斯还说毕达哥拉斯创立了纯数学，把它变成一门高尚的艺术。

　　毕达哥拉斯学派常把数描绘成沙滩上的点子或小石子。他们按点子或小石子所能排列而成的形状来把数进行分类。例如，1，3，6和10这些数叫三角形数，因为相应的点子能排列成正三角形（如下图）。

第四个三角形数10特别令毕达哥拉斯学派神往，因为这是他们所珍爱的数，并且这三角形的每边有4点，而4又是另个得宠的数。他们认识到1，1+2，1+2+3等这些和数都是三角形数，并且知道

1+2+…+n=n(n+1)/2。

　　1，4，9，16，…这些数他们称之为正方形数，因为用点表示时可把它们排成正方形（如下图）

。不是正方形数的复合数（非质数）是长方形数（它的点不能排成正方形，但能排成长方形）。

　　把代表数的点子排成几何图形后，整数的一些性质就变得很明显。例如在上图的第三个图形中画了一道斜杠之后，便可看出连续两个三角形数之和是个正方形数。这是普遍成立的，用现代记法如下

。按当时的数学学术水平，毕达哥拉斯学派不太可能证明这个一般结论。

　　毕达哥拉斯派再用下图

所示的方案从一个正方形数得出下一个正方形数。图中折线右方和下方的那些点所形成的数，他们称作一个gnomon。他们通过这图得到一般的结论，用现在的记号表示出来就是

n²+(2n+1)=(n+1)²

。其次，若从1起加上gnomon3，再加上gnomon5等，其结果用现在的记号来表示便是

1+3+5+…+(2n-1)=n²。

　　“gnomon”这个字在巴比伦人的原意可能是指日规（日晷）

上的直杆，用它的阴影来指示时刻。然而，古希腊毕达哥拉斯所处的年代，gnomon指木匠用的方尺（直角尺）。现在这工具还在使用的，如下图

。所以，毕达哥拉斯就用“gnomon”表示从正方形的一角割掉一个小正方形后所余的图形

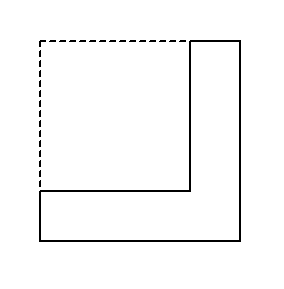
。后来，欧几里得又把“gnomon”表示从平行四边形一角割掉一个较小的相似平行四边形后所余的图形

。

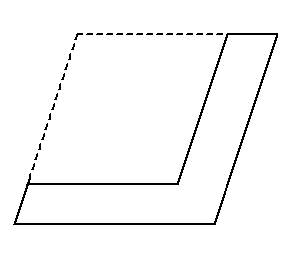　　毕达哥拉斯派还研究多角数，如五边形数

，每个点代表数1。由图可看出第一个五边形数是1，第二个（其各点排成个五角形的顶点）是5，第三个数是1+4+7即12等。第n个五边形数，现在的写法是

1+4+7+...+3n-2=(3n²-n)/2。

同样有六边形数

是1，6，15，28，…而一般第n个六边形数，现在的写法是

1+5+9+...+4n-3=2n²-n，

和其他多边形数。

　　若一数等于它的所有因数（包括1，但不包括该数本身）之和，他们称之为完全数，如6的因数是

1, 2, 3, 6，

然而

1+2+3=6，

所以6是完全数；又如28的因数是

1, 2, 4, 7, 14, 28，

然而

1+2+4+7+14=28，

所以28是完全数；又如496的因数是

1, 2, 4, 8, 16, 31, 62, 124, 248, 496，

然而

1+2+4+8+16+31+62+124+248=496，

所以496是完全数。数本身大于其因数之和的叫盈数，小于其因数之和的则叫亏数。若有两数彼此等于另一数的因子之和，他们称这两数是亲和数，例如284的因数是

1, 2, 4, 71, 142, 284，

然而

1+2+4+71+142=220，

220因数是

1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220，

然而

1+2+4+5+10+11+20+22+44+55+110=284，

所以，284与220是亲和数。

　　毕达哥拉斯派发现，若m是奇数，则三元数组m，(m²-1)/2及(m²+1)/2可排成直角三角形三边，即勾股数（毕达哥拉斯三元数组）。他们发现的这个算法虽然只给出一部分勾股数（毕达哥拉斯三元数组），但足以说明，他们已知道勾股定理（毕达哥拉斯定理）。

　　毕达哥拉斯派研究了质数、递增数列，以及他们认为美的一些比和比例关系。例如，若p和q是两数，它们的算术平均值A是

(p+q)/2，

几何平均值G是

√pq（p与q的积的算术平方根），

而调和平均值H，即1/p和1/q的算术平均值取倒数，是

2pq/(p+q)。

由于

(p+q)/2 × 2pq/(p+q) = pq，

所以，G是A和H的几何平均值。A/G=G/H，算术平均值与几何平均值的比等于几何平均值与调和平均值之比叫完全比例。又由于

p : A = p : (p+q)/2 = 2p/(p+q)，

H : q = 2pq/(p+q) : q = 2p/(p+q)，

所以，p：A=H：q，一个数与算术平均值之比等于调和平均值与另一数之比叫音乐比例。

　　毕达哥拉斯派所说的数仅指整数。和现代人不一样，他们不把两个整数之比看成是一个分数而是另一类数。实际的分数是用于商业上的，以表示钱币或度量单位的若干部分，但商业上的这类应用算术不属于正统希腊数学范畴。以至于，当毕达哥拉斯派发现有些比——例如等腰直角三角形斜边与一直角边之比或正方形对角线与其一边之比——不能用整数之比表达时，他们就感到震惊和不安，甚至愤怒。由于毕达哥拉斯派关心能形成直角三角形三边的三元整数组，他们很可能是在做这项工作时发现这些新比的。他们把那些能用整数之比表达的比称作可公度比，意即相比两量可用公共度量单位量尽，而把不能这样表达的比称作不可公度比。例如现写成√2/2（根号2比2）的比便是不可公度比。希腊人也把不可公度量之比称作αλογοζ（alogos，“非逻辑，不能表达”）或αρρητοζ（arratos，“没有比”）。

　　后人把不可公度比的发现归功于米太旁登的希帕苏斯（Hippasus，公元前5世纪）。相传当时毕达哥拉斯派的人正在海上，就因这一发现而把希帕苏斯投到海里，因为他的发现否定了毕达哥拉斯派对宇宙解释的信条——宇宙间的一切现象都能归结为整数或整数之比（注意：现在看来这是荒谬的）。

　　后来，毕达哥拉斯派给出了√2与1不可公度的证明。他们用的是归谬法，即间接证法。证明过程如下：

　　设等腰直角三角形斜边（c）与一直角边（a）之比为c:a，并设c与a是互质数。于是根据勾股定理（毕达哥拉斯定理）得

c²=2a²。

又由于c²为偶数，然而任一奇数的平方必是奇数

(2n+1)²=4n²+4n+1

，所以c必然也是偶数。由于c和a是互质数，因此a必然是奇数。由于c是偶数，故可设

c=2b。

于是

c²=4b²=2a²。

因此

a²=2b²，

这样a²是个偶数，于是a也是偶数。但a同时又是奇数，这就产生了矛盾。

　　现代数学中用无理数来表示不可公度比。但毕达哥拉斯派不愿意接受这样的数。巴比伦人和埃及人没有无理数这一概念的，毕达哥拉斯派则至少认识到不可公度比与可公度比的性质完全不同。

　　在发现不可公度比之前，毕达哥拉斯派是把数与几何等同起来的，之后他们再也无法这样干了。他们虽然还探讨几何及几何中的比，但对于数的比则只限于考察可公度比。

　　一些几何规律的发现也归功于毕达哥拉斯派的。最出名的是勾股定理（毕达哥拉斯定理）

。

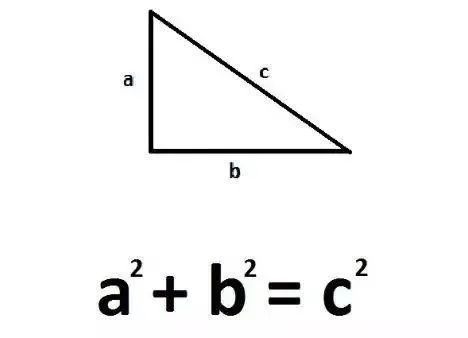人们认为我们所学的关于三角形、平行线、多边形、圆、球和正多面体的一些定理也是毕达哥拉斯派发现的。特别是他们知道三角形三角之和是180°。关于相似形的部分规律，以及平面可被等边三角形、正方形和正六边形所平铺，都是毕达哥拉斯派的研究结果。

参考资料：

《古今数学思想》【美】莫里斯·克莱因