牛吃什么？大家一定知道牛吃草。那神吃什么？大多数人都会回答不知道。因为牛是实际的动物，所以有大家都认识的属性——吃草；但神是虚构的，至于吃什么这种实在的属性，自然是没有的。我们初中学的平面几何，也就是欧几里得几何，在这方面就非常谨慎——在研究某种几何图形的性质之前，一定有确实的把握这种图形一定存在。避免研究“神吃什么”的问题。那么欧几里得是如何做到的呢？

　　欧几里得接受把公理和公设区分开了的观点，认为公理是所有科学中的真理；公设是某个学科的条件，至于公设是否为真，只能看它推导出来的结果是否正确。下面是《几何原本》第一卷的公设（注：这里的直线是线段。）：

1、由任意一点到另外任意一点可以画直线；

2、一条有限直线可以继续延长；　

3、以任意点为心及任意的距离可以画圆；

4、凡直角都彼此相等；

5、同平面内一条直线和另外两条直线相交，若在某一侧的两个内角的和小于二直角，则这二直线经无限延长后在这一侧相交。

　　实质上，我们现在也把这些公设当作公理来使用。欧几里得总结这五点公设，无非是为了规范他研究的几何范围，避免研究不存在的几何图形，提出荒谬可笑的结论。

　　古希腊数学家们发现：只用无刻度的直尺和圆规作图，就能作出公设的图形及有这些图形构成的复杂图形，这种作图方法叫做尺规作图，这种图形的生成方法是构造法。在欧几里得几何里只有角平分线的性质，但没有角的三分的性质。尽管角的三分线显然存在，但可能是不能用尺规作图法三分一个角的缘故。

　　画一条线段等于已知线段a。在工程应用中，先量出线段a的长度，再画一条等于这个长度的线段；在数学中，我们用尺规作图，如下图，

我们可以用直尺画射线AC，再用圆规在射线AC上截取AB=a。这就是“作一条线段等于已知线段”的尺规作图。

　　比较两条线段的长短。工程应用上，我们用刻度尺分别测量出它们的长度来比较。在几何中，如下图，

用圆规把其中的一条线段移到另一条上作比较。由图可知，点A与点C重合，点B落在C，D之间，这时我们说线段AB小于线段CD，记作AB<CD。B与D点重合时，我们说线段AB等于线段CD，记作AB＝CD。B落在C，D之外这时我们说线段AB大于线段CD，记作AB>CD。

　　线段的和与差。如下图，在直线上作线段AB=a，再在AB的延长线上作线段BC=b，线段AC就是a与b的和，记作AC=a+b。设线段a>b，如果在线段AB上作线段BD=b，那么线段AD就是a与b的差，记作AD=a-b。

　　线段的等分点。如下图4，点M把线段AB分成相等的两条线段AM与MB，点M叫做线段AB的中点（midpoint）。类似地，还有线段的三等分点、四等分点等。

课堂练习１

1、估计下列图中线段AB与线段AC的大小关系（大于、小于或等于），再用圆规来检验你的估计。

2、如下图，已知线段a，b，作一条线段，使它等于2a-b。

3、如下图，点D是线段AB的中点，C是线段AD的中点，若AB=4cm，求线段CD的长度。

　　两点的所有连线中，线段最短。简单说成：两点之间，线段最短。连接两点间的线段的长度，叫做这两点的距离（distance）。要注意了，什么是“两点的距离”。

课堂练习2

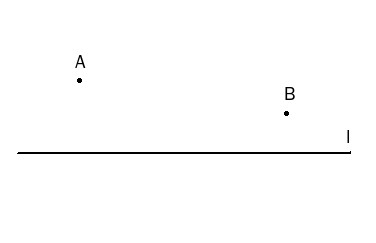
１、如下图，用尺规作图，在直线l上求一点C，使CA+CB最小。

参考资料：

１、《几何原本》【古希腊】欧几里得　著　兰纪正　朱恩宽　译

２、《古今数学思想》【美】莫里斯·克莱因　著　张理京　张锦炎　江泽涵　译