观察下面视频,
剪刀剪开布片过程发现,握紧剪刀的把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小,直到剪开布片。这个连三岁小孩都懂的,为何还要在初中数学了说啊。事实上,每个人都是天生的几何家,只不过多数人不自觉而已。数学上把剪刀的构造抽象化,看作是两条相交的直线,这样,剪刀的问题就变成两条相交直线所成的角的问题。
【探究1】
任意画两条相交的直线,形成四个角,如下图

∠1和∠2有怎样的位置关系?∠1和∠3呢?
分别量一下各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?2和∠4呢?2和∠3呢?3和∠4呢?∠4和∠1呢?在剪刀把手之间的角变化的过程中,这个关系还保持吗?为什么?
∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为邻补角(adjacent angles on a straight line)。
∠1和∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角(opposite angles)。
∠1与∠2互补,∠3与∠2互补,由“同角的补角相等”,可以得出∠1=∠3。类似地,∠2=∠4。这样,我们得到对顶角的性质:
对顶角相等。
例1 如下图,

直线a,b相交,∠1=40°求∠2,∠3,∠4的度数。
解:由邻补角的定义,得∠2=180°-∠1=180°-40°=140°;
由对顶角相等,得
∠3=∠1=40°,
∠4=∠2=140°。
【练习】
如图,

取两根木条a,b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型。你能说出其中的一些邻补角与对顶角吗?两根木条所成的角中,如果∠α=35°,其他三个角各等于多少度?如果∠α等于90°,115°,m°呢?
在相交线的模型(上面练习插图)中,固定木条a,转动木条b。当b的位置变化时,a,b所成的∠α也会发生变化。当∠α和它的邻补角相等时,a与b互相垂直(perpendicular),记作a⊥b。(课本中的定义是不恰当的,本处采用欧几里得《几何原本》中的定义。)

垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另条直线的垂线(perpendicular line),它们的交点叫做垂足(foot of a perpendicular)。在下图中,AB⊥CD,垂足为O。
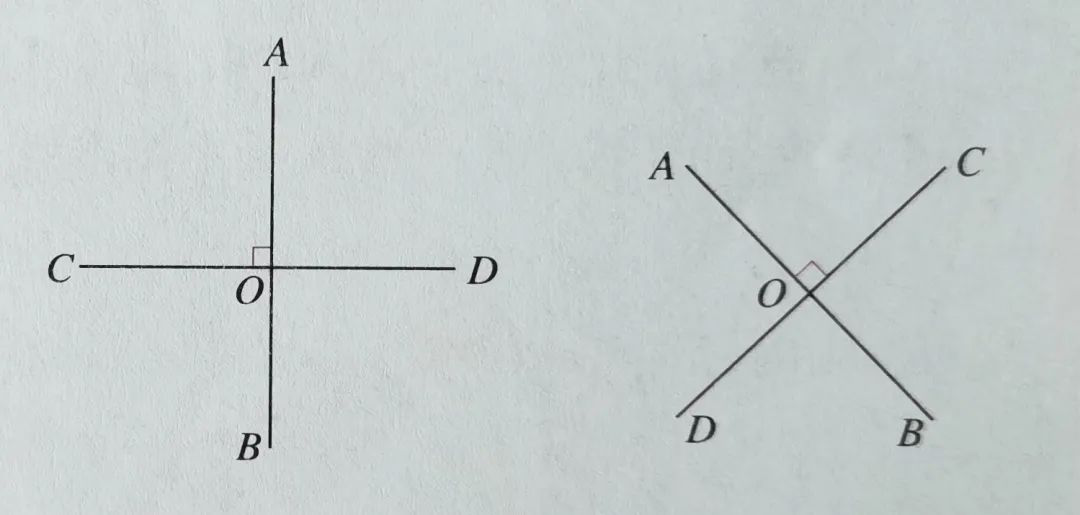
因为一个角与它的邻补角的和是一个平角,两条直线垂直时它们相等,所以每个角都是半个平角——直角。可见,如果两条直线相交所成的四个角中的任意一个角是直角(在角度制中是90°,在弧度制中是π/2),那么这两条直线垂直。综合上面对垂直的描述,在上图中,判断垂直的推理过程可以写成下面几种形式:
(1)互邻补角相等(垂直定义)
因为∠AOC和∠AOD互为邻补角,并∠AOC=∠AOD,
(或
因为∠AOC和∠BOC互为邻补角,并∠AOC=∠BOC,
因为∠AOD和∠BOD互为邻补角,并∠AOD=∠BOD,
因为∠BOC和∠BOD互为邻补角,并∠BOC=∠BOD,
)
所以AB⊥CD。
(2)一角为直角
因为∠AOC(或∠AOD,∠BOC,∠BOD)是直角,
所以AB⊥CD。
(3)一角为90°(角度制)
因为∠AOC(或∠AOD,∠BOC,∠BOD)=90°,
所以AB⊥CD。
(4)一角为π/2(弧度制)
因为∠AOC(或∠AOD,∠BOC,∠BOD)=π/2,
所以AB⊥CD。
日常生活中,两条直线互相垂直的情形很常见,说出下图

中的一些互相垂直的木条。举出你生活中遇到的其他垂直例子。
【探究】
(1)用一把三角尺和一把直尺画已知直线l的垂线,这样的垂线能画出几条?
(2)用一个量角器和一把直尺画已知直线l的垂线,这样的垂线能画出几条?
(3)用一个圆规和一把直尺画已知直线l的垂线(尺规作图),这样的垂线能画出几条?
(4)用尺规作图法,经过直线l上一点A能画出几条垂线?
(5)用尺规作图法,经过直线l外一点B能画出几条垂线?
经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线。即
在同一平面内,过一点有且只有一条直线与已知直线垂直。
【练习】
1、画一条线段或射线的垂线,就是画它们所在直线的垂线,如下图,

请你过点P画出射线AB或线段AB的垂线。
【思考】
如下图,

在灌溉时,要把河中的水引到农田P处,如何挖渠能使渠道最短?
【探究】
如下图,

连接直线l外一点P与直线l上各点O,A1,A2,A3,…,其中PO⊥l(我们称PO为点P到直线l的垂线段)。比较线段PO,PA1,PA2,PA3,…的长短,这些线段中,哪一条最短?
连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:垂线段最短。
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
【练习】
如下图,

三角形ABC中,∠C=90°。
(1)分别指出点A到直线BC,点B到直线AC的距离是哪些线段的长;
(2)三条边AB,AC,BC中哪条边最长?为什么?
参考资料:
1、《几何原本》【古希腊】欧几里得 著 兰纪正 朱恩宽 译