仔细观察下面一些美丽的图案，
它们有什么共同的特点？能否根据其中的一部分绘制出整个图案？也就是说，它是不是一个图形密铺后的图形？【探究】
如何在一张半透明的纸上，画出一排形状和大小如下图
的雪人呢？
可以把半透明的纸盖在图上，先描出一个雪人，然后按同一方向陆续移动这张纸,再描出第二个、第三个……(如下图)。
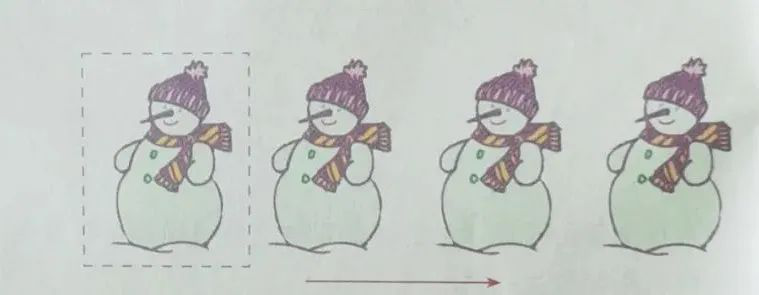
【思考】
如下图，
在所画出的相邻两个雪人中，找出三组对应点（例如，它们的鼻尖A与A′，帽顶B与B'，纽扣C与C'），连接这些对应点，观察得出的线段，它们的位置、长短有什么关系？
可以发现,AA'//BB'//CC'，并且AA′=BB′=CC‘.再画出一些连接其他对应点的线段，它们是否仍有前面的关系？【归纳】
1. 把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同。
2. 新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点，连接各组对应点的线段平行（或在同一条直线上）且相等。
图形的这种移动，叫做平移（translation）。
图形平移的方向，不限于是水平的，如下图。
平移在我们日常生活中是很常见的，利用平移也可以制作很多美丽的图案。你能举出生活中一些利用平移的例子吗？
例 如下图，
平移三角形ABC，使点A移动到点A'，画出平移后的三角形A'B'C'。
分析：图形平移后的对应点有什么特征？作出点B和点C的对应点B'，C'，能确定三角形A'B'C'吗？解：如下图，
连接AA'，过点B作AA'的平行线l，在l上截取BB′=AA'，则点B‘就是点B的对应点。
类似地，你能作出点C的对应点C"，并进一步得到平移后的三角形A'B'C'吗？动手试一试。本文用《五行星Python几何画板》完成，见附录1。
【习题】【复习巩固】1. 下列图案可以由什么图形平移形成？
2. 如下图，
有一个由4个三角形组成的图形，通过平移，你能用它组成什么图案？试试，把你的图案与同学们交流一下。3. 如下图，
在方格纸中平移三角形ABC，使点A移到点M，点B和点C应移到什么位置？再将点A由点M移到点N，分别画出两次平移后的三角形，如果直接平移三角形ABC，使点A移到点N，它和我们前面得到的三角形位置相同吗？
【综合运用】
4. 如下图，
用平移方法说明怎样得出平行四边形的面积公式S=ah。
5. 许多美丽的图案都是用平移的方法绘制而成的。观察下面图案
的绘制规律，你能类似地设计一些图案吗？
【拓广探索】
6. 如下图，
在一块长为a m，宽为b m的长方形草地上，有一条弯曲的小路，小路的左边线向右平移1m就是它的右边线，求这块草地的绿地面积。
附录1：
下载《五行星Python几何画板》http://www.5xstar.com/down/jhhb/pyjhhb.zip解压到5xstar/jtrclient/pysrc/jhhb中。
把图片加工成400x400的sjx.gif图片放到5xstar/jtrclient/pysrc中。
在《五行星学编程》中运行5xstar/jtrclient/pysrc/jhhb/idlemain.py。等界面初始化完成后，在《五行星Python几何画板》idle端输入下面代码：
>>> stl.register_shape("pysrc/sjx.gif")
>>> stl.shape("pysrc/sjx.gif")
>>> stl.setpos(0, 0)
>>> stl.stamp()
用《五行星Python几何画板》的界面端打点A，B，C，A'，用标签功能显示这四点的位置坐标，然后用下面的代码作图：
>>> import math
>>> headangle=math.atan2(170+49,66-32)*180/math.pi
>>> length=math.sqrt((170+49)**2+34**2)
>>> stl.setpos(32,-49)
>>> stl.seth(headangle)
>>> stl.down()
>>> stl.fd(length)
>>> stl.up()
>>> stl.setpos(-155,-142)
>>> stl.down()
>>> stl.fd(length)
>>> posB1=stl.pos()
>>> stl.up()
>>> stl.dot()
>>> stl.setpos(80,-140)
>>> stl.down()
>>> stl.fd(length)
>>> stl.dot()
>>> posC1=stl.pos()
>>> stl.pensize(2)
>>> stl.setpos(66,170)
>>> stl.setpos(posB1)
>>> stl.setpos(posC1)