观察下图

中的图片，其中的房屋结构、蜂巢结构等给我们以由一些线段围成的图形的形象。你能从图中想象出几个由一些线段围成的图形吗？

　　我们学过三角形。类似地，在平面内，由一些线段首尾顺次相接组成的封闭图形叫做多边形（polygon）。

　　多边形按组成它的线段的条数分成三角形、四边形、五边形……三角形是最简单的多边形。如果一个多边形由n条线段组成，那么这个多边形就叫做n边形。如下图，

螺母底面的边缘可以设计为六边形，也可以设计为八边形。

　　多边形相邻两边组成的角叫做它的内角。下图

中的∠A，∠B，∠C，∠D，∠E是五边形ABCDE的5个内角。多边形的边与它的邻边的延长线组成的角叫做多边形的外角。下图

中的∠1是五边形 ABCDE的一个外角。

　　连接多边形不相邻的两个顶点的线段，叫做多边形的对角线（diagonal）。下图

中，AC，AD是五边形ABCDE的两条对角线。

【课堂练习】

上图五边形ABCDE共有几条对角线？请画出它的其他对角线。

　　如下图，

画出四边形ABCD的任何一条边（例如CD）所在直线，整个四边形都在这条直线的同一侧，这样的四边形叫做凸四边形。而下图

中的四边形ABCD就不是凸四边形，因为画出边CD（或BC）所在直线，整个四边形不都在这条直线的同一侧。类似地，画出多边形的任何条边所在直线，如果整个多边形都在这条直线的同一侧，那么这个多边形就是凸多边形。本节只讨论凸多边形。

　　我们知道，正方形的各个角都相等，各条边都相等。像正方形这样，各个角都相等，各条边都相等的多边形叫做正多边形（regular polygon）。下图

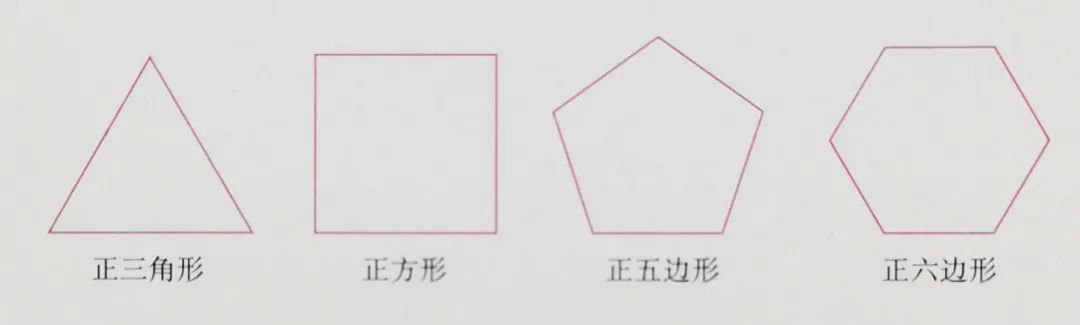
是正多边形的一些例子。

【练习】

1.　画出下列多边形的全部对角线：

2.　四边形的一条对角线将四边形分成几个三角形？从五边形的一个顶点出发，可以画出几条对角线？它们将五边形分成几个三角形？

【思考】

　　我们知道，三角形的内角和等于180°，正方形、长方形的内角和都等于360。那么，任意一个四边形的内角和是否也等于360°呢？你能利用三角形内角和定理证明四边形的内角和等于360°吗？

　　为了探讨这个问题，用《几何画板》画一个任意四边形，计算它的内角和，然后改变四边形的形状，看看内角和有无改变。录屏视频如下：

可见，四边形内角和保持在360.00°不变。

　　要用三角形内角和定理证明四边形的内角和等于360°，只要将四边形分成两个三角形即可。

　　如下图，

在四边形ABCD中，连接对角线AC，则四边形ABCD被分为△ABC和△ACD两个三角形。

　　由此可得

　　∠DAB+∠B+∠BCD+∠D

　　=∠1+∠2+∠B+∠3+∠4+∠D

　　=(∠1+∠B+∠3)＋(∠2+∠4+∠D)

　　∵　∠1+∠B+∠3=180°，

　　　　∠2+∠4+∠D=180°，

　　∴　∠DAB+∠B+∠BCD+∠D=180°+180°=360°。

即四边形的内角和等于360°。

　　类比上面的过程，你能推导出五边形和六边形的内角和各是多少吗？

　　观察下图，

填空：

　　从五边形的一个顶点出发，可以作______条对角线，它们将五边形分为______个三角形，五边形的内角和等于180°×______。

　　从六边形的一个顶点出发，可以作______条对角线,它们将六边形分为______个三角形，六边形的内角和等于180°×______。

　　通过以上过程，你能发现多边形的内角和与边数的关系吗？

　　一般地，从n边形的一个顶点出发，可以作(n-3)条对角线，它们将n边形分为(n-2)个三角形，n边形的内角和等于180°×(n-2)。

　　这样就得出了多边形内角和公式:

　　n边形内角和等于(n-2)×180°。

【课堂练习】

　　把一个多边形分成几个三角形，还有其他分法吗？由新的分法，能得出多边形内角和公式吗？

　　例 1　如果一个四边形的一组对角互补，那么另一组对角有什么关系？

　　解：如下图，

在四边形ABCD中，

∠A+∠C=180°。

　　∵　∠A+∠B+∠C+∠D=(4-2)×180°=360°，

　　∴　∠B+∠D=360-(∠A+∠C)

　　　　　　　=360-180°=180°。

　　这就是说，如果四边形的一组对角互补，那么另一组对角也互补。

　　例 2　如下图，

在六边形的每个顶点处各取一个外角，这些外角的和叫做六边形的外角和。六边形的外角和等于多少？

　　分析：考虑以下问题：

　　(1)　任何一个外角同与它相邻的内角有什么关系？

　　(2)　六边形的6个外角加上与它们相邻的内角，所得总和是多少？

　　(3)　上述总和与六边形的内角和、外角和有什么关系？

　　联系这些问题，考虑外角和的求法解。

　　解：六边形的任何一个外角加上与它相邻的内角都等于180°。因此六边形的6个外角加上与它们相邻的内角，所得总和等于6×180°。

　　这个总和就是六边形的外角和加上内角和。所以外角和等于总和减去内角和，即外角和等于

6×180°-(6-2)×180°=2×180°=360°。

【思考】

　　如果将例2中六边形换为n边形(n是不小于3的任意整数)，可以得到同样结果吗？

　　由上面的思考可以得到：

　　多边形的外角和等于360°。

　　你也可以像以下这样理解为什么多边形的外角和等于360°。

　　如下图，

从多边形的一个顶点A出发，沿多边形的各边走过各顶点，再回到点A，然后转向出发时的方向。在行程中所转的各个角的和，就是多边形的外角和。由于走了一周，所转的各个角的和等于一个周角，所以多边形的外角和等于360°。请看《几何画板》中的演示结果：

　　利用多边形外角和恒定是360°这个特点，很容易就得到多边形内角和。由于一个外角和它的互补内角和是180°，对于n边形，一共有n对这样的互补角，它们的总和是n×180°，减去外角和360°，得n边形内角和是n×180°-360°，即(n-2)×180°。

【练习】

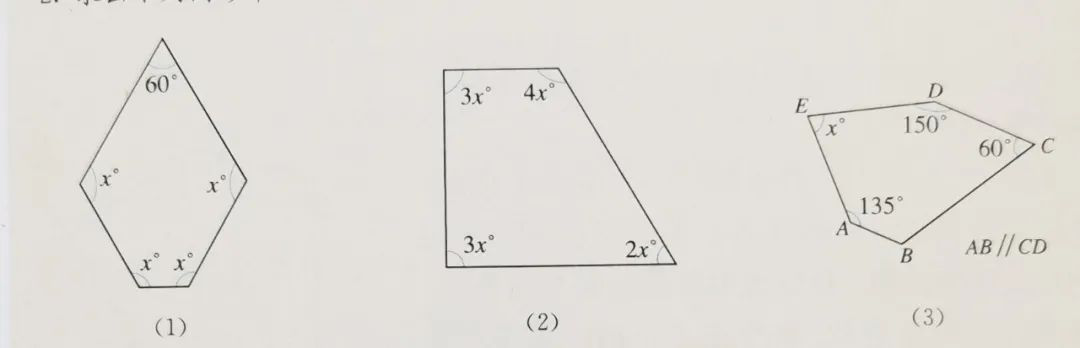
1.　求出下列图形中x的值：

2.　一个多边形的各内角都等于120°，它是几边形？

3.　一个多边形的内角和与外角和相等，它是几边形？

【习题】

【复习巩固】

1画出下面多边形的全部对角线：

2.　求出下列图形中x的值：

3.　填表:

4.　计算正五边形和正十边形的每个内角的度数。

5.　一个多边形的内角和等于1260°，它是几边形？

6.　(1)　一个多边形的内角和是外角和的一半，它是几边形？

　　(2)　一个多边形的内角和是外角和的2倍，它是几边形？

【综合运用】

7.　如下图，

在四边形ABCD中，∠A=∠C，∠B=∠D，AB与CD有怎样的位置关系？为什么？

8.　如下图，

BC⊥CD，∠1=∠2=∠3，∠4=60°，∠5=∠6。

　　(1)　CO是△BCD的高吗？为什么？

　　(2)　∠5的度数是多少？

　　(3)　求四边形ABCD各内角的度数。

【拓广探索】

9.　如下图，

五边形ABCDE的内角都相等，且∠1=∠2，∠3=∠4，求x的值。

10.　如下图，

六边形ABCDEF的内角都相等，∠DAB=60°。AB与DE有怎样的位置关系？BC与EF有这种关系吗？这些结论是怎样得出的？

【化归思想】

　　这里利用多边形内角和的计算来说明化归数学思想。一个ｎ边形的内角和问题比较复杂，不能一下解决，如下图，

过隔一个顶点的两个顶点切一个三角形下来，被切下的三角形内角和是180°，剩下的是n-1多边形。重复切下三角形，直到剩下的也是三角形为止。累计切下的三角形内角和与剩下的一个三角形内角和就是n边形内角和。

(n-3)×180°+180°=(n-2)×180°。

【递归算法】

　　一些化归思想解决的问题，可以用递归算法编程解决。下面是Python代码：

【递归算法练习】

　　用递归法计算1/2+1/4+1/8+...+1/2^n的值，把下图代码涂灰的地方补上代码。