下图

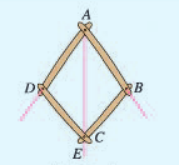
是一个平分角的仪器，其中AB=AD，BC=DC.将点A放在角的顶点，AB和AD沿着角的两边放下，沿AC画一条射线AE，AE就是这个角的平分线。你能说明它的道理吗？

　　也许你的直觉AC就是角平分线，但要说明它的道理，必须从已知的公理和定理出发取阐释。在阐释之前，我们需要把用自然语言描述的问题转化为数学描述：在∠BAD的两边上取两点B，D，使AB=AD，以大于½BD为半径，分别以B，D为圆心作圆，两个圆的其中一个交点是C，过C作射线AE是∠BAD的平分线。如下图所示。

　　分析：证明AE是∠BAD的平分线，即要证明∠BAC=∠DAC，由于圆B和圆D的半径相等，所以BC=DC，即∠BAC和∠DAC是一对等边的对角，如果能证明△ABC≌△ADC。这样问题就转化为证明△ABC≌△ADC，由于△ABC和△ADC的公共边AC相等，BC=DC，AB=AD，由全等三角形的“边边边”标准得证。证明过程与分析过程方向相反。

　　证明：在△ABC和△ADC中，

　　∵　AC=AC，　

　　　　BC=DC，

　　　　AB=AD，

　　∴　△ABC≌△ADC。（SSS）

　　∵　BC=DC，　

　　　　∠BAC和∠DAC分别是BC和DC的对角，

　　∴　∠BAC=∠DAC。

　　∴　AE是∠BAD的平分线。

　　只用无刻度的直尺和普通圆规作图，叫做尺规作图。上面的过程也说明了角平分线的尺规作图方法。

　　已知：∠AOB，

　　求作：∠AOB的平分线。（尺规作图）

　　作法：(1)以点O为圆心，适当长为半径画弧，交OA于点M,交OB于点N。

　　(2)分别以点M，N为圆心，大于½MN的长为半径画弧，两弧在∠AOB的内部相交于点C。

　　(3)画射线OC。射线OC即为所求（如下图）。

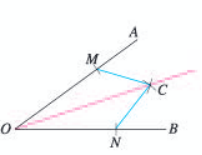
　　如下图，

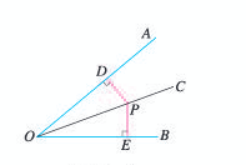
任意作一个角∠AOB，作出∠AOB的平分线OC。在OC上任取一点P，过点P画出OA,OB的垂线，分别记垂足为D，E，测量PD，PE并作比较，发现PD=PE你得到什么结论，在OC上再取几个点也能得到相同的结果。

　　我们猜想角的平分线有以下性质：

　　角的平分线上的点到角的两边的距离相等。

　　上面的命题只是从有限的点中归纳出来的，如果要使它成为定理就要用已知公理和以证明的定理去证明它。

　　分析：OC是∠AOB的平分线，所以∠DOP=∠EOP，PD和PE是它们的对边，如果Rt△DOP≌Rt△EOP，那问题解决。由于公共边OP都是斜边（即直角的对边），符合角角边标准，得证。

　　证明：∵　PD⊥OA，PE⊥OB，

　　∴　∠PDO=∠PEO=90°。

　　在△PDO和△PEO中，

　　∠PDO=∠PEO，

　　∠AOC=∠BOC，

　　OP=OP，

　　∴　△PDO≌△PEO(AAS)。

　　∵　∠DOP=∠EOP，PD和PE是它们的对边，

　　∴　PD=PE。

　　一般情况下，我们要证明一个几何命题时，可以按照类似的步骤进行，即

　　0、如果原题是用自然语言描述的，先在内心或草稿纸上用数学语言描述；

　　1、明确命题中的已知和求证；

　　2、根据题意，画出图形，并用符号表示已知和求证；

　　3、从求证开始逆向分析，直到充分条件已知；

　　4、从已知的充分条件开始，与分析的过程相反，写出证明过程。

　　“角的平分线上的点到角的两边的距离相等。”的逆命题是“角的内部到角的两边距离相等的点在平分线上。”上面我们已经证明了命题，但逆命题是否成了，还需要证明。

　　逆命题的数学语言陈述：点P是∠AOB内的一点，P到OA和OB的距离PD=PE，求证P在∠AOB的平分线OC上。

　　分析：如果P在∠AOB的平分线OC上，那么连接OP，就需要∠DOP=∠DOP，即需要Rt△PDO≌Rt△PEO。由斜边、直角边全等标准得证。至于角平分线的唯一性可以通过反证法。

　　证明：连接OP，在Rt△PDO≌Rt△PEO中，

　　∵　OP=OP，

　　　　PD=PE，

　　∴　Rt△PDO≌Rt△PEO，（HL）

　　∵　PD=PE，∠DOP和∠EOP是它们的对角，

　　∴　∠DOP＝∠EOP，

　　即　射线OP是角的平分线。

　　假设P不在OC上，

　　如果在OC上方，即∠DOP<∠DOC，

　　∵　∠DOP＝½∠DOE，∠DOC½∠DOE，

　　∴　½∠DOE<½∠DOE。

　　然而，½∠DOE=½∠DOE，得假设P在OC上方不成立；

　　同理，假设P在OC下方也不成立；

　　∴　Ｐ必然在OC上。

　　逆命题成立：

　　角的内部到角的两边距离相等的点在平分线上。

　　如下图，

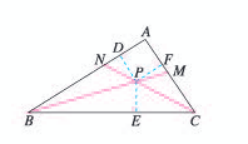
△ABC的角平分线BM，CN相交于点P。

　　求证：点P到三边AB，BC，CA的距离相等.

　　证明：过点P作PD，PE，PF分别垂直于AB，BC，CA，垂足分别为D，E，F。

　　∵　BM是∠ABC的角平分线，点P在BM上，

　　∴　PD=PE。

　　同理PE=PF。

　　∴　PD=PE=PF。

　　即点P到三边AB，BC，CA的距离相等.

　　进一步求证：三角形的3条角平分线相交于一点。

　　分析：三角形的2条角平分线必相交于一点，如果这个交点在第3条角平分线上，那么条角平分线必相交于这一点。由于角内到两边的距离相等的点在角平分线上，那么只要证明这一点到第3个角的两边距离相等，由上面的证明，可以得证。

　　证明：过点P作PD，PE，PF分别垂直于AB，BC，CA，垂足分别为D，E，F。

　　∵　BM是∠ABC的角平分线，点P在BM上，

　　∴　PD=PE。

　　同理PE=PF。

　　∴　PD=PF。

　　∵　角的内部到角的两边距离相等的点在平分线上，

　　∴　P点在∠BAC的平分线上，

　　即三角形的3条角平分线相交于一点。