对称是全等形在空间中的位置关系，因此两个图形或一个图形分开的两部分，首先是两个全等形。下面以平面图形来讨论对称。

　　一般情况下，我们可以认为平面图形是由点构成的，在平面直角坐标系中，点由两个坐标来规定：横坐标x和纵坐标y。把x或y改成相反数、把x和y都改成相反数，就得到了3个影子点，如下图所示。

　　四点之间的连线分为2种，一种是过原点被原点分为相等的两段——中心对称；一种不过原点只垂直于x轴或y轴而且被x轴或y轴平分的两段——轴对称。对于两个全等形，如果它们的每一个对应点符合中心对称，那么它们是成中心对称；如果它们的每一个对应点符合轴对称，那么它们成轴对称。如下图所示。

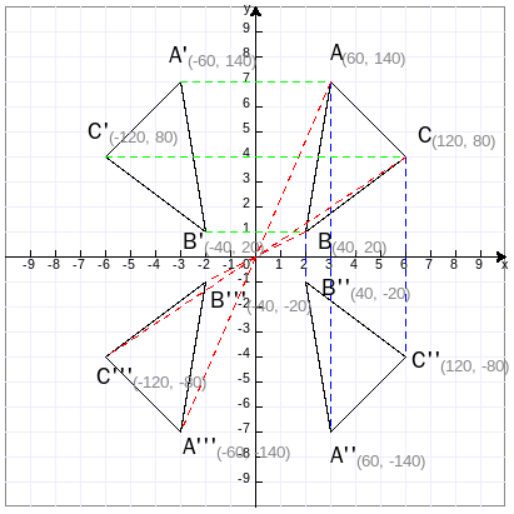
　　△ABC与△A'B'C'是以y轴为对称轴成图形轴对称；△ABC与△A''B''C''是以x轴为对称轴成轴对称；△ABC与△A'''B'''C'''是以原点(0,0)成中心对称。

　　在视觉上（不具备数学严谨性）：

　　把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线（成轴）对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点(symmetric points)。

　　把一个图形绕着某一点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这点（成中心）对称，这点叫做对称中心，旋转后重合的点是对应点，叫做对称点(symmetric points)。

　　这里并不打算展开中心对称的讨论，下面只讨论轴对称。

　　我们考察上图中的△ABC与△A'B'C'，发现通过平移和旋转无法使它们重叠在一起，只有通过翻转才可以。那是不是所有的成轴对称的两个图形都只有翻转才能重叠呢？我们先考察等腰三角形。下面使用《五行星Python几何画板》制作视频。代码附录１。

进度条，百分之18

　　由于平移也能使等腰三角形重叠，则离y轴近的点移动的距离比翻转的大，离y轴远的点移动的距离比翻转的小，那么必然存在一些点平移和翻转的距离是一样的。

　　证明：设左等腰三角形上有一点(-a,b)，a>0，那么右等腰三角形上必有一对称点(a,b)。假如平移的距离是c（c>0），那么翻转与平移距离差是c-2a。若c-2a=0，得a=½c。意思就是说，对于左等腰三角形，在x=-½c直线上的点平移和翻转的距离是一样的。

　　显然，用x=-½c直线分开等腰三角形为两部分，这两部分以x=-½c直线成轴对称。我们把这种至少可以找到一条经过图形本身的对称轴成轴对称的图形叫做轴对称图形。如果一个图形通过平移和旋转能与它的翻转后的图形重叠，这个图形是轴对称图形。

　　图形（成）轴对称是两个图形的位置关系，轴对称图形是图形的本身性质。可把图形分为两种：轴对称图形和非轴对称图形。轴对称图形在小学阶段已经学过了。下一节课将讨论非轴对称图形。

　　练习题１：判定对错，如果错了请举出至少一个反例。

（１）两个图形轴对称，那么这两个图形一定全等。　

（２）两个图形全等，那么这两个图形一定轴对称。

（３）两个图形轴对称，那么这两个图形都是轴对称图形。

（４）两个轴对称图形全等，必然存在一条直线使它们轴对称。

（５）一个图形与它绕图形外一点旋转30°后的图形，不可能存在一条直线使它们成轴对称。

（６）轴对称图形最多一条对称轴。

（７）一个图形平移后能与它的（成）轴对称的图形重叠，这个图形是轴对称图形。

（８）一个图形与一个轴对称图形成轴对称，这个图形一定是轴对称图形。

（９）一个图形翻转后，通过平移或旋转能与原图形重叠，这个图形一定是轴对称图形。

强基初中数学&学Python——第141课 全等三角形小结/活动/复习题

强基初中数学&学Python——第140课 角的平分线的性质

强基初中数学&学Python——第139课　全等三角形的判定

强基初中数学&学Python——第138课　全等三角形及其性质

精品课程推荐：

Python数据结构与算法——第五十五课 自然数字典式基数排序（本书结束篇）

　　学思营编程课堂基于蓝桥STEM86平台https://www.stem86.com，开展学编程三部曲：Scratch（三年级以前）>>>Python（四年级以后）>>>C++（七年级以后）教育实验活动，任何人可以免费参加，打开https://xuesiying.stem86.com网页注册进入课堂，也可关注本公众号留言。

更多课程请打开“学思营”同步网站：http://5xstar.com

附录１：

#等腰三角形自定义海龟
'''
idlemain.py打开的命令行中输入：
stl.up()  #提笔
stl.setpos(-150,0)  #绘制自定义海龟的顶角，平躺的等腰三角形
getShape(stl)  #获取自定义海龟
stl.fillcolor("blue")  #改变填充颜色为蓝色
stl.seth(0)  #改变海龟方向为水平向前
stl.setpos(110,-50)  #把海龟放到右侧
clears()  #清除画布图形
stl.stamp()  #印下一个海龟
stl.bk(220)  #后退220变为以y轴为对称轴的对称图形
stl.fillcolor("red")  #改变填充颜色为红色
stl.st()  #显示海龟
for i in range(1,221):  #水平移动海龟使其与右侧的印章重叠
    stl.fd(1)  
'''
from math import sin,pi  #导入正弦函数和圆周率
def getShape(stl):  #获取自定义海龟, stl非复制海龟
    stl.seth(-35)  #顶角70°的一半
    stl.down()  #下笔
    pos = stl.pos()  #记录开始位置
    stl.begin_poly()  #开始记录多边形
    stl.fd(150)  #前进150
    stl.left(125)  #左转
    stl.fd(2*150*sin(35/180*pi))  #画底边
    stl.setpos(pos)  #回出发点
    stl.end_poly()  #结束记录
    myPoly = stl.get_poly()  #提取多边形
    stl.register_shape("ta",myPoly)  #注册形状
    stl.shape("ta")  #换上自定义形状海龟
    stl.up()  #提笔