我们知道，有两边相等的三角形是等腰三角形(isosceles triangle)。下面，我们利用轴对称的知识来研究等腰三角形的性质。

　　如下视频，

，时长05:07

　　通过上面的观察，我们发现等腰三角形的性质：

　　性质1　等腰三角形的两个底角相等（简写成“等边对等角”）；

　　性质2　等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合（简写成“三线合一”）。

　　通过观察得到的结论需要证明。我们可以利用三角形的全等证明这些性质。

　　如下图，

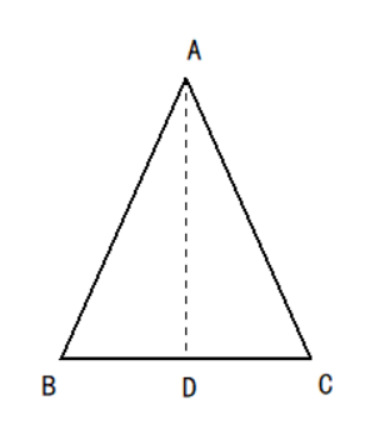
△ABC中，AB=AC，作底边BC的中线AD。

　　∵　AB=AC，

　　　　BD=CD，

　　　　AD=AD，

　　∴　△BAD≌△CAD　(SSS)。

　　∴　∠B=∠C。

　　这样，我们就证明了性质1。

　　由△BAD≌△CAD，还可得出∠BAD=∠CAD，即AD是∠BAC的平分线；和∠BDA=∠CDA，从而AD⊥BC。这也就证明了等腰三角形ABC底边上的中线AD平分顶角∠BAC并垂直于底边BC。

　　△ABC中，AB=AC，作底边BC的高AD。

　　∵　AB=AC，

　　　　∠BAD=∠CDA=90°，

　　　　AD=AD，

　　∴　△BAD≌△CAD　(HL)。

　　∴　BD=DC，∠BAD=∠CAD。

　　即，底边上的高平分顶角并且平分底边。

　　△ABC中，AB=AC，作∠BAC的角平分线。

　　∵　AB=AC，

　　　　∠BDA=∠CAD，

　　　　AD=AD，

　　∴　△BAD≌△CAD　(SAS)。

　　∴　BD=DC，∠BDA=∠CDA。

　　即，顶角的平分线平分底边并且垂直于底边。

　　这也就证明了性质2。

　　从以上证明也可以得出，等腰三角形底边上的中线的左右两部分经翻折可以重合，等腰三角形是轴对称图形，底边上的中线（顶角平分线、底边上的高)所在直线就是它的对称轴。

　　例1　如下图，

在△ABC中，AB=AC，点D在AC上，且BD=BC=AD。求△ABC各角的度数。

　　分析：三角形虽然有三个内角，但由于内角和是180°，所以三个内角只有两个自由度，又由于等腰三角形的两个底角相等，这样就剩下一个自由度，由于BD把等腰三角形分为两个等腰三角形，∠BDC=∠BCD=2∠A，自由度为0，问题得解。

　　解：在△BCD中，

　　∵　BC=BD，

　　∴　∠C=∠BDC；

　　又　在△BDA中，

　　∵　BD=AD，

　　∴　∠ABD=∠A；

　　∵　∠BDC=∠A+∠ABD，(三角形外角等于另两个内角和)

　　∴　∠C=2∠A；

　　又　在△ABC中，

　　∵　AB=AC，

　　∴　∠C=∠ABC；

　　∵　∠A+∠ABC+∠C=180°，(三角形内角和等于180°)

　　∴　5∠A=180°，

　　∴　∠A=36°，

　　　　∠ABC=72°，

　　　　∠C=72°。

　　练习题1：

1.　如下图，在下列等腰三角形中，直接写出它们的底角的度数。

2.　如下图，△ABC是等腰直角三角形(AB=AC，∠BAC=90°)，AD是底边BC上的高。标出∠B，∠C，∠BAD，∠DAC的度数，并写出图中所有相等的线段。

3.　如下图，在△ABC中，AB=AD=DC，∠BAD=26°。求∠B和∠C的度数。

　　我们知道等腰三角形的两个底角相等，那么反过来，有两个角相等的三角形是不是等腰三角形（有两条边相等）呢？

　　反证法分析：如下图，在△ABC中，∠ABC=∠C，假如这两个角的对应边不相等，不失一般性，设AC＞AB，在AC截取AD=AB，连接BD，则△ABD是等腰三角形，则∠ABD=∠ADB，可以得到矛盾：∠ABD>∠ABC（部分大于全部），得证。

　　反证法证明：∵　假设AC＞AB，在AC截取AD=AB，

　　连接BD，得等腰△ABD，

　　∴　 ∠ABD=∠ADB，

　　又　∠ADB=∠DBC+∠C，∠ABC=∠ABD+∠DBC，

　　∴　∠C<∠ADB=∠ABD<∠ABC，

　　即　∠C<∠ABC，与条件相悖，所以AC＞AB是不可能的。

　　同理，AC<AB也是不可能的。

　　所以AC=AB，△ABC是等腰三角形。

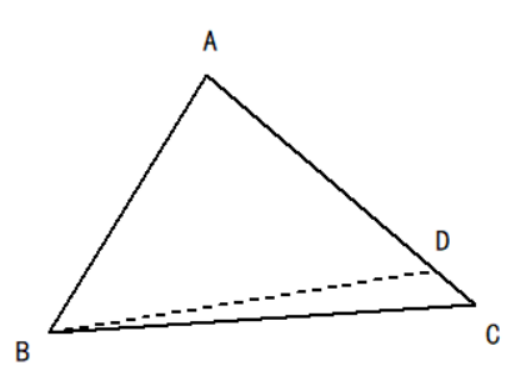
　　轴对称法分析：如下图，在△ABC中，∠B=∠C，以三角形外的一条直线l为对称轴得到它的对称图形△A'C'B'，由于两个三角形符合ASA全等标准，那么得到AB=A'C'，又由于轴对称的性质得A'C'=AC，得证。

　　证明：作△ABC关于它外面的一条直线的对称图形△A'C'B'，

　　∵　∠B=∠C，∠C=∠C'，

　　∴　∠B=∠C'，

　　同理，∠C=∠B'，

　　又　BC=C'B'，

　　∴　 △ABC≌△A'C'B'，（ASA）

　　∴　AB=A'C'，

　　又　A'C'=AC，（轴对称的两边）

　　∴　AB=AC，

　　即△ABC是等腰三角形。

　　轴对称图形法分析：如下图，在△ABC中，∠B=∠C。作△ABC的角平分线AD。由于∠B和∠C对应的边是公共边，△BAD和△CAD符合AAS全等标准，得证。

　　证明：作△ABC的角平分线AD，在△BAD和△CAD中，

　　∵　∠1=∠2，

　　　　∠B=∠C，

　　　　AD=AD，

　　∴　△BAD≌△CAD  (AAS)，

　　∴　AB=AC，

　　即 △ABC是等腰三角形。

　　由上面推证，我们可以得到等腰三角形的判定方法：

　　如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”)。

　　例2　求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形。

　　已知：如下图，∠CAE是△ABC的外角，∠1=∠2，AD//BC。

　　求证：AB=AC。

　　分析：要证明AB=AC，可先证明∠B=∠C。因为∠1=∠2，所以可以设法找出∠B，∠C与∠1，∠2的关系。

　　证明：∵AD//BC，

　　∴　∠1=∠B（平行线同位角相等），

　　　　∠2=∠C（平行线内错角相等）。

　　又　∵　∠1=∠2，

　　∴ 　∠B=∠C。

　　∴　AB=AC（等角对等边）。

　　例3　如下图，已知等腰三角形底边长为a，底边上的高的长为h，求作这个等腰三角形。

　　分析：只知底和高，不能确定一个三角形，但这些三角形中只有一个等腰三角形，因为等腰三角形的顶角在底的垂直平分线上。

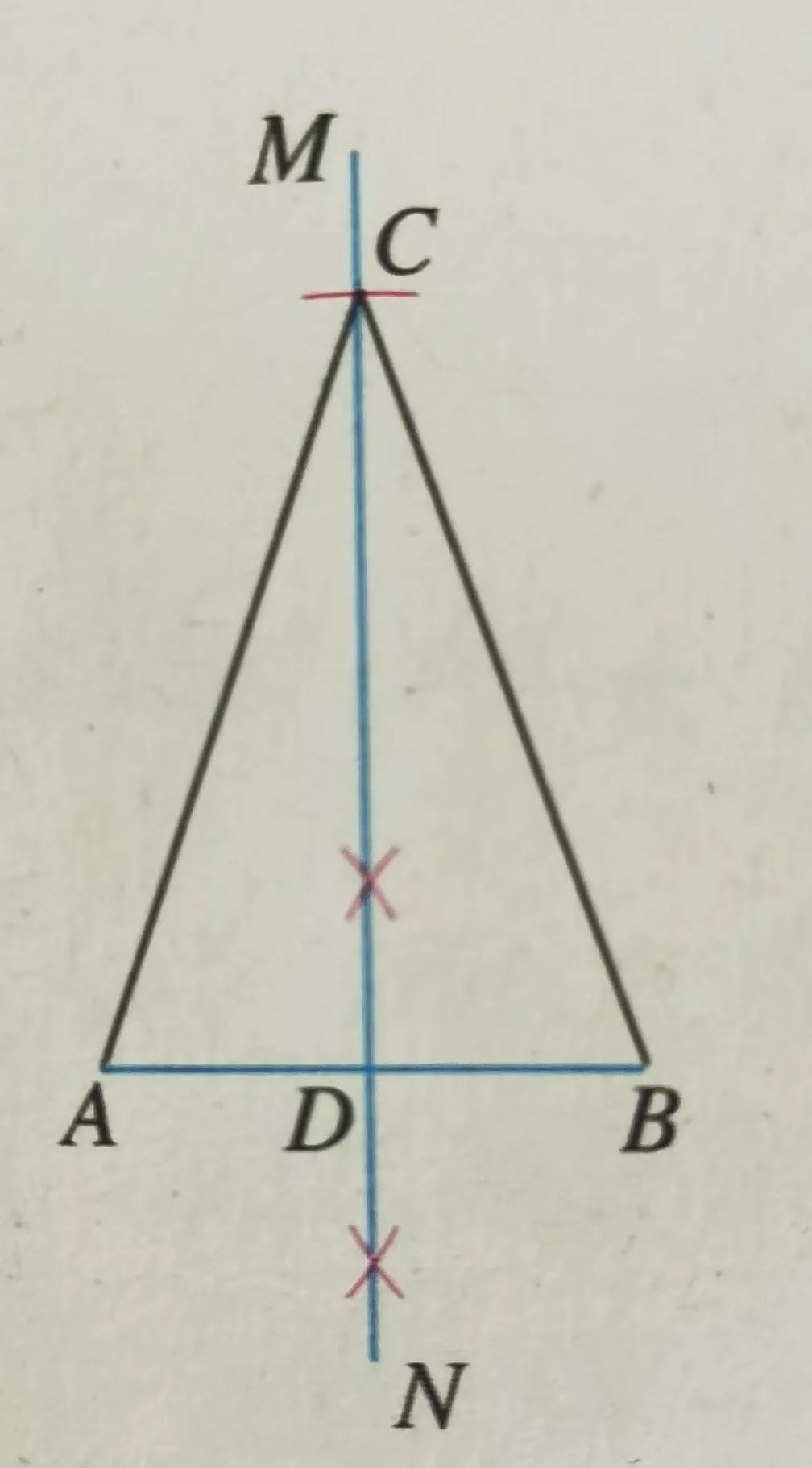
　　作法：(1)作线段AB=a。

　　(2)作线段AB的垂直平分线MN，与AB相交于点D。

　　(3)在MN上取一点C,使DC=h。

　　(4)连接AC，BC，则△ABC就是所求作的等腰三角形。如下图。

　　证明：在△ADC和△BDC中，

　　∵　AD=BD，

　　　　∠ADC=∠BDC=90°，

　　　　DC=DC，

　　∴　△ADC≌△BDC（SAS），

　　∴　AC=BC，即△ABC是等腰三角形。

　　练习题2：

1.　如下图，∠A=36°，∠DBC=36°，∠C=72°，分别计算∠1，∠2的度数，并说明图中有哪些等腰三角形。

2.　如下图，把一张长方形的纸沿对角线折叠，重合部分是一个等腰三角形吗？为什么？

3.　求证：如果三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形。

4.　如下图，AC和BD相交于点O，且AB//DC，OA=OB。求证OC=OD。

5.　求证：如果三角形一个角的平分线垂直于对边，那么这个三角形是等腰三角形。

6.　求证：如果三角形一边的高平分它的对角，那么这个三角形是等腰三角形。

7.　请观看下面的视频，

，时长00:45

求证：如果三角形一个角的平分线平分对边，那么这个三角形是等腰三角形。