前面我们研究过一些关于“两点的所有连线中，线段最短”“连接直线外一点与直线上各点的所有线段中，垂线段最短”等的问题，我们称它们为最短路径问题。

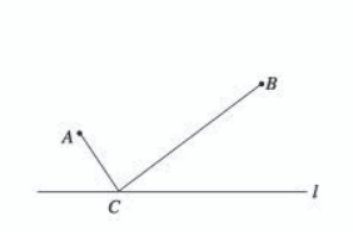
　　问题1　如下图，牧马人从A地出发，到一条笔直的河边l饮马，然后到B地。牧马人到河边的什么地方饮马，可使所走的路径最短？

　　首先把问题转化为一个数学语言描述的问题。如下图，如果把河边l近似地看成一条直线，C为直线l上的一个动点，那么，上面的问题可以转化为：当点C在I的什么位置时，AC与CB的和最小。

　　请看下面的视频：

，时长00:50

　　从视频中可以看到，距离和开始变小，后来变大，期间确实有一个最小值。但这是一条折线，显然不符合“两点的所有连线中，线段最短”和“连接直线外一点与直线上各点的所有线段中，垂线段最短”。如何才能把折线问题转化为这两个最短线路问题呢？

　　假如牧马人的朋友在B处等他，他的朋友不知道牧马人从哪里出发的。当牧马人到达B处后，他的朋友问他走了多少路程，牧马人只回答走了9.85千米。他的朋友以为他从什么地点出发呢？

　　很自然，如下图，延长BC到A'点，使CA'=CA，这样问题就转化为A与A'的关系。

　　很明显，A'是A关于直线l的对称点，C是在A'到B的直线与直线l的交点。问题就转化为当C不在A'到B的直线与直线l的交点上时，路径都比A'B大。

　　如下图，当C在C'处时，由于l是AA'的垂直平分线，所以C'A'=C'A，由△BA'C'可知C'A'+C'B>BA'，即路径变长了。

　　例题1：如下图，假如A地离河岸是1千米，B地离河岸2千米，A地到B地的距离在河岸的投影是4千米，求A地经河岸到B地的最短距离。

　　解：如下图，以直线l为对称轴作A点的对称点A'，连接CA'，得

　　CA'=CA；

　　连接BA'，交l于C'，在△BCA'中，

　　CA'+CB>A'B。

　　当C从A'B左侧到右侧与C'点重合时，CA+CB最小，等于A'B。

　　过A'作l的平行线，交BQ延长线于O点，则

　　BO=BQ+AP=1+2=3（千米）。

　　在Rt△BA'O中，

　　斜边A'B²=3²+4²，

　　所以 A'B=5（千米）。（勾股定理）

　　答：最短距离是5千米。

　　这个问题似乎与我们的生活没有什么关系，不是的，我们每天都要照镜子，就是光通过镜子反射，传到我们的眼睛成像的结果。所以最短距离问题，在光学里就是反射定律：

　　反射光线与入射光线与法线在同一平面上；反射光线和入射光线分居在法线的两侧；反射角等于入射角 。

　　时空对于我们来说是可以感知的，感知的基础是我们认为光在真空中总是直线传播的。对于光的受体，是无法分辨光是直接从光源直线传过来还是经过反射传过来的。因此，虽然经过反射，但光还是按最短距离传播。即符合上面的最短距离数学规律。

　　用数学语言描述反射定律：

　　如下图，已知：CB、CA和CD是同一平面端点是C的三条射线，CB、CA分处CD两侧，直线l垂直于CD，垂足是C。求证：∠ACD=∠BCD。

　　分析：基于基本的物理事实——光是直线传播的，因此视光源必定在BC的延长线上，即A点关于镜面l的轴对称点A'。由轴对称性质可得∠ACP=∠A'CP，又对顶角∠BCQ=∠A'CP，CD⊥l得证。

　　证明：由光是直线传播的和最短路径可知，C(反射点)必然是A'(视光源)与B(受体)的连线和镜面l的交点。

　　∵ A'(视光源)是A(光源)的关于镜面l的轴对称点，

　　∴ ∠ACP=∠A'CP，

　　又 ∠A'CP=∠BCQ，

　　∴ ∠ACP=∠BCQ，

　　又 ∵CD⊥l

　　∴ ∠PCD=∠QCD，

　　∴ ∠PCD-∠ACP=∠QCD-∠BCQ，

　　即 ∠ACD=∠BCD。

　　这个充分说明，最短路径问题实际就是光的反射问题。

　　如果河岸是半圆弧状，我们可以借助光的反射定律来计算最短路径问题。

　　练习题1：

　　请看下面的视频：

，时长00:45

　　如下图，用《几何画板》作出最短路径并证明。

　　问题2　（造桥选址问题）如下图，A和B两地在一条河的两岸，现要在河上造一座桥MN。桥造在何处可使从A到B的路径AMNB最短？（假定河的两岸是平行的直线，桥要与河垂直。)

　　如下图，我们可以把河的两岸看成两条平行线a和b，N为直线b上的一个动点，MN垂直于直线b，交直线a于点M。这样，上面的问题可以转化为下面的问题：当点N在直线b的什么位置时，AM+MN+NB最小？

　　观看下面的视频：

，时长00:30

　　从视频中观察到AM//NB时，总路程最小。

　　由于河岸宽度是固定的，因此当AM+NB最小时，AM+MN+NB最小。这样，问题就进一步转化为：当点N在直线b的什么位置时，AM+NB最小？

　　显然，AM+NB是忽略了河宽（河宽变0），A和B的距离，当它们在同一直线上时就是最小值了。只有AM与NB平行，才能在河宽变0时在一条直线上。

　　要证明，先描述成一个完整的数学命题。

　　如下图，A，B分别位于平行线l1和l2的外侧，MN是平行线l1和l2之间的垂线段，M位于A侧的l1上，N位于B侧的l2上。求证：当AM//NB时，AM+MN+NB最小。

　　分析：过A作河的垂线AA'，AA'等于河宽（《几何画板》可以通过任意平行四边形定位）。连接A'和B，交于河B侧的N，则河的垂线段NM就是桥的位置。由于MN是不变的，即求证AM+NB最小。用平行四边形可以构构造AM+NB是三角形的一边，其它位置是是三角形的两边。

　　证明：如下图，

　　过A作l1的垂线，与BN的延长线交于A'，

　　∵ MN⊥l1，AA'⊥l1，

　　∴ MN//AA'，

　　又∵ AM//NB，

　　∴ 得平行四边形AA'NM。

　　∴  AM=A'N，

　　∴ AM+NB=A'B。

　　假设另外两点N'M'，

　　∵ AA'=MN=M'N'，且AA'//M'N，

　　∴ 得平行四边形AA'N'M'。

　　∴ AM'=A'N'，

　　∵ A'N'+N'B>A'B，

　　∴ A'N'+N'B>AM+NB。

　　即 当AM//NB时，AM+MN+NB最小。

　　例题2：利用上面的结果，如下图，假如AB对直线l1的投影距离是6，A到l1的距离是3，l1与l2的距离是2，B到l2的距离是5，求AM+MN+NB最小值。

　　解：∵ A'B²=6²+(3-2+2+5)²，（勾股定理）

　　∴ A'B=10，

　　∴ AM+MN+NB最小值=10+2=12。

　　练习题2：

　　请看下面的视频：

，时长00:55

　　视频中看到，桥不是垂直河岸，而是保持60°，AM+MN+NB仍然有最小值。如下图，用《几何画板》作出最短路径并证明，然后计算它的实数值。

　　总结

　　在解决最短路径问题时，我们通常利用轴对称、平移等变化把问题转化为容易解决的问题（两点直线段最短；三角形两边和大于第三边；点到直线的连线，垂线段最短；三角形中大角对大边。），从而作出最短路径的选择。