请看下面的图形：

　　这三个图形看起来很“对称”，但它们既不是轴对称也不是中心对称。如果旋转不小于2的偶数次一周形成的图形，是中心对称图形，但它们都是旋转不小于3奇数次一周，所以我们需要扩充“中心对称图形”为“旋转对称图形”，以适配所有“旋转“特性的对称图形。

　　一般地，如果一个图形绕着某点O旋转角α后所得到的图形与原图形重合，则称此图形关于点O有角α的旋转对称。

　　如下图，如果把旋转对称图形分为360/α份后，相邻的两份中，每对对称点与旋转中心的连线相等，它们的夹角都相等，并等于α。

　　下图是具有旋转对称性质的一些图形。

　　如下图，如果一个图形是中心对称图形，则把它绕对称中心旋转180°后所得图形与原来图形重合，所以，中心对称图形关于其对称中心有180°的旋转对称。因此中心对称图形一定是旋转对称图形。

　　如下图，把正n边形绕着它的中心旋转360°/n的整数倍后所得的正n边形与原正n边形重合，正n边形关于其中心有360°/n的旋转对称。当n是偶数是，该正n边形是中心对称图形，否则不是。

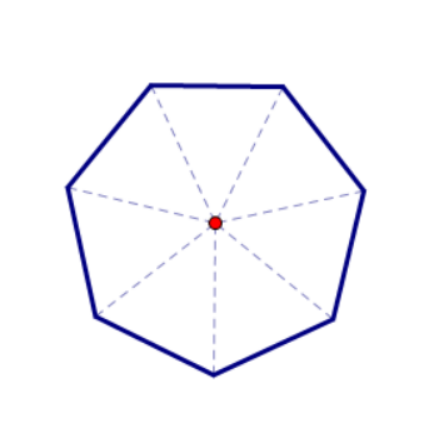
　　圆关于圆心有任意角的旋转对称，许多物体呈圆形就是应用了圆的这种性质。当我们用一个扳手扳转一个正六边形螺母时，要应用正六边形关于其中心有60°的整数倍的旋转对称，也要应用圆关于圆心有任意角的旋转对称。

　　旋转中的坐标

　　如下图，旋转对称的对称点在直角坐标系中的坐标关系，旋转角α>0逆时针，α<0表示顺时针，P(x,y)旋转α后变为P'(x',y')。P'(x',y')和P(x,y)到原点的距离相等，OP'的倾角比OP大α。

　　设OP长度为r，倾角是β，那么P'的坐标(x',y')符合下面的关系：

r²=x²+y²，①

x'=rcos(α+β)，②

y'=rsin(α+β)，③

x=rcos(β)，④

y=rsin(β)。⑤

由和角公式：

cos(α+β)=cos(α)*cos(β)-sin(α)*sin(β)，⑥

sin(α+β)=sin(α)*cos(β)+cos(α)*sin(β)。⑦

把④⑤代入⑥⑦，得

cos(α+β)=(x/r)cos(α)-(y/r)sin(α)，⑧

sin(α+β)=(x/r)sin(α)+(y/r)cos(α)。⑨

把⑧⑨代入②③，得旋转坐标关系公式：

x'=xcos(α)-ysin(α)，

y'=xsin(α)+ycos(α)。

　　下面验证（初中需要掌握的三个坐标公式）。（1）如果α=180°，sin(α)=0，cos(α)=-1，即中心对称，

x'=-x，

y'=-y。

（2）如果α=90°，sin(α)=1，cos(α)=0，即逆时针转90°，

x'=-y，

y'=x。

（3）如果α=-90°，sin(α)=-1，cos(α)=0，即顺时针转90°，

x'=y，

y'=-x。

　　不失一般性，限定x>0和y>0，如下图可以看到它们坐标的关系（记住这幅图片）。

　　练习题1：

1.　在平面直角坐标系中，点A的坐标是(-3,2)，作点A关于x轴的对称点，得到点B,再作点B关于y轴的对称点，得到点C。点A与点C有什么关系？如果点A是平面内任一点，即坐标是(x,y)，点A与点C也有同样关系吗？

2.　把点P(x,y)绕原点分别顺、逆时针旋转90°，180°，270°，360°，点P的对应点的坐标分别是什么？将结果填入下表。