在圆中，除圆心角外，还有一类角（如下图中的∠ACB)，它的顶点在圆上，并且两边都与圆相交，我们把这样的角叫做圆周角(angle in a circular segment)。

　　如下图，连接AO，BO，得到圆心角∠AOB。可以发现，∠ACB与∠AOB对着同一条弧AB，它们之间存在什么关系呢？

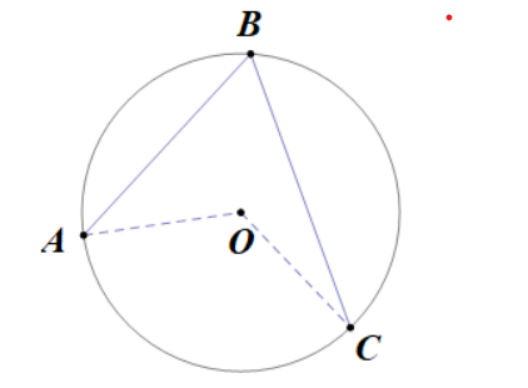
　　请看下面的视频。

，时长00:15

　　通过观看视频，可以发现，同弧所对的圆周角的度数等于这条弧所对的圆心角的度数的一半。

　　如下图，为了证明上面发现的结论，在⊙O任取一个圆周角∠BAC，过AO作一直线l，由于点A的位置不同，直线l会：

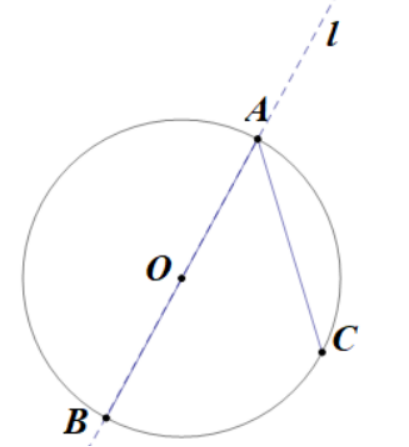
　　(1)在圆周角的一条边上，如下图；

　　(2)在圆周角的内部，如下图；

　　(3)在圆周角的外部，如下图。

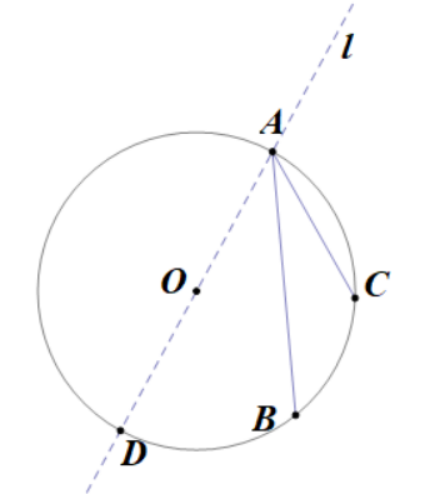
　　如下面证明中的图。我们来分析第(1)种情况。圆心O在∠BAC的一条边上，圆心角∠BOC是等腰三角形AOC的顶角的外角，圆周角是等腰三角形的一个底角，得证。

　　对于第(2)种情况，直径AD把圆周角和圆心角都分为两个角，每对角都符合第(1)种情况，得证。

　　对于第(3)种情况，直径AD把圆周角和圆心角都补上符合第(1)种情况的一对角后，扩大了的那对角也符合第(1)种情况，得证。

　　证明：过AO作直线l，

　（1）如下图，l在圆周角的边BA上，连接OC，在△AOC中，

　　∵　∠BOC是∠AOC的外角，

　　∴　∠BOC=∠BAC+∠OCA。

　　又　∵　OA=OC，

　　∴　△AOC是等腰三角形，

　　∴　∠BAC=∠OCA，

　　∴　∠BOC=2∠BAC。

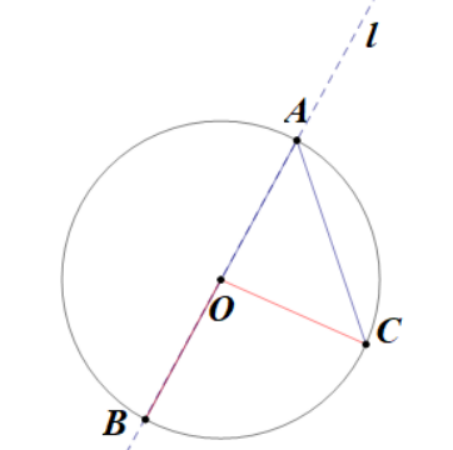
　　（2）如下图，l在圆周角的内部，连接OB，OC，

　　∠BAC=∠BAD+∠CAD，∠BOC=∠BOD+∠COD，

　　∵　由（1）的证明，同理可得

　　∠BOD=2∠BAD，∠COD=2∠CAD，

　　∴　∠BOD+∠COD=2(∠BAD+∠CAD)，

　　∴　∠BOC=2∠BAC。

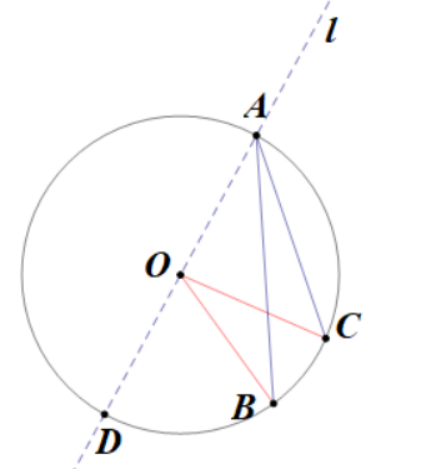
　　（3）如下图，l在圆周角的外部，连接OB，OC，

　　∠BAC=∠DAC-∠DAB，∠BOC=∠DOC-∠DOB，

　　∵　由（1）的证明，同理可得

　　∠DOC=2∠DAC，∠DOB=2∠DAB，

　　∴　∠DOC-∠DOB=2(∠DAC-∠DAB)，

　　∴　∠BOC=2∠BAC。

　　这样，我们就得到圆周角定理：

　　一条弧所对的圆周角等于它所对的圆心角的一半。

　　进一步，我们还可以得到下面的推论：

　　同弧或等弧所对的圆周角相等。

　　半圆（或直径）所对的圆周角是直角，直角的圆周角所对的弦是直径（如下图）。

　　课堂练习1：证明上面两条推论。

　　例4　如下图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于点D，求BC，AD，BD的长。

　　分析：AB是直径，则△ACB和△ADB都是直角三角形，由条件BC可求；但△ADB有两条边未知，只有一种情况可求——等腰，由于两边所对的弧的圆周角相等得证。

　　解：如下图，

　　连接OD。

　　∵　AB是直径，

　　∴　∠ACB=∠ADB=90°.

　　在Rt△ABC中，

　　BC=√AB²-AC²=√10²-6²=8(cm)。

　　∵　CD平分∠ACB，

　　∴　∠ACD=∠BCD，

　　∴　∠AOD=∠BOD。

　　∴　AD=BD。

　　又　在Rt△ABD中，

　　　　AD²+BD²=AB²，

　　∴　AD=BD=AB/√2=10/√2=5√2(cm)。

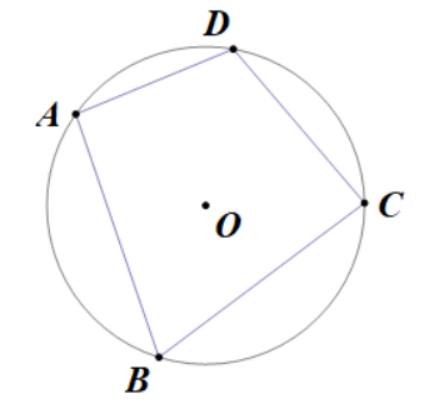
　　如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆。如下图，四边形ABCD是⊙O的内接四边形，⊙O是四边形ABCD的外接圆。

　　圆内接四边形的四个角之间有什么关系？请看下面的视频。

，时长00:30

　　从视频中发现对角互补的结论，下面证明这个结论。

　　因为圆内接四边形的每一个角都是圆周角，所以我们可以利用圆周角定理，来研究圆内接四边形的角之间的关系。

　　如下图，连接OB，OD。

　　∵　∠A所对的弧为弧BCD，∠C所对的弧为弧BAD，

　　又　弧BCD和弧BAD所对的圆心角的和是周角，

　　∴　∠A+∠C=360°/2=180°.

　　同理　∠B+∠D=180°.

　　这样，利用圆周角定理，我们得到圆内接四边形的一个性质：

　　圆内接四边形的对角互补。