如下图，AB是正n边形的一条边，OA和OB是半径，半径长是R，OD是边心距。

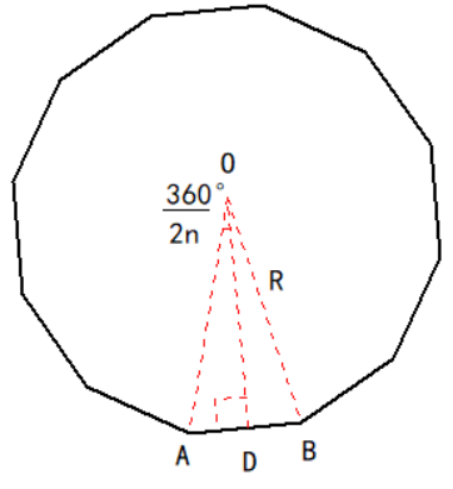
　　那么中心角是360°/n，它的一半是360°/2n，由此得到正多边形的周长公式：

C=n·2·R·sin(360°/2n)=2Rnsin(360°/2n)。

　　由上面的等式两边同时除以2R，得

C/2R=nsin(360°/2n)，

是一个与半径无关的数。

　　请看下面的视频。

，时长01:19

　　从视频中可以看出，当n增大时，图形趋向圆。事实上，一些作图软件也是用边数足够大的正多边形来作圆（例如，Python海龟画图）。C/2R，即nsin(360°/2n)，当n增大时，值趋向我们熟悉的一个数3.14159......圆周率π。

　　π是一个无理数。

　　证明π是无理数已超出初中数学的范围。π是圆的周长与直径之比，它是无理数，只是说明圆的周长C和直径D不可公度，并非是周长不可以是有理数。

　　历史上，对于圆周率π的研究是古代数学一个经久不衰的话题，在我国，东汉初年的《周髀算经》里就有“径一周三”的古率。公元前3世纪，古希腊数学家阿基米德(Archimedes，约公元前287一前212)通过圆内接和外切正多边形逼近圆周的方法，得到圆周率介于3(10/71)和3(1/7)之间。

　　我国魏晋时期的数学家刘徽(263年左右)首创“割圆术”，利用圆的内接正多边形来确定圆周率，并指出在圆的内接正多边形边数加倍的过程中“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体，而无所失矣”他计算出π=157/50≈3.14。

　　南朝的祖冲之(429一500)在公元5世纪又进一步求得π的值在3.1415926和3.1415927之间，是第一个将圆周率的计算精确到小数点后7位的人。

　　随着时代的发展，人们利用高等数学的知识来计算π的值，先后得出了许多计算π的公式，π的近似值的位数也迅速增长。

　　电子计算机问世以后，圆周率的计算突飞猛进，π的小数点后的位数不断增长、20世纪50年代得到千位以上，60年代则达到50万位，80年代得到10亿位，到21世纪初，科学家已计算出π的小数点后超过万亿的位数。

　　当今时代，π的计算成为测试超级计算机的各项性能的方法之一，运算速度与计算过程的稳定性对计算机至关重要，这正是超高精度的π的计算直到今天仍然有重要意义的原因之一。