活动1：设计400m田径比赛跑道

　　如下图，设计一条8道的400m跑道，每条跑道由两条直的跑道和两端是半圆形的跑道组成，每条跑道宽1m，每条直跑道是100m，最内侧的跑道长度为400m。如果大家都从终点线起跑，外圈的运动员就要跑更多的路程，显然不公平。因此，为了公平比赛，在外侧跑道的运动员的起跑点必须前移。那么每条跑道要前移多少米，就是要完成的任务。

　　活动2：车轮做成圆形的数学道理

　　路上行驶的各种车辆，车轮基本是圆形的，为什么车轮要做成圆形的呢？这里面有什么数学道理吗？请看下面的视频。

，时长00:20

可以发现，圆在转动过程中，圆心与切线的距离始终是不变的，这个距离等于圆的半径。因此，把车轮做成圆形，当车轮在平坦的地面上滚动时，车轮中心与地面的距离保持不变，坐车的人会感到非常平稳。如下图。

　　如果车轮是正方形形状的，情况会怎样呢？请看下面的视频。

，时长00:55

　　可见，正方形的中心不断升高和降低。试想一下，如果把车厢装在过轮子中心的轴上，车辆在平坦的路面上行驶时，采用正方形的车轮，你会有什么感觉？

　　活动3：探究四点共圆的条件

　　我们知道，过任意一个三角形的三个顶点能作一个圆，过任意一个四边形的四个顶点能作一个圆吗？

　　可以认为四边形由两个有一边相等的三角形合并而成，因此与三点作圆相似，作四条边的垂直平分线，如果交于一点，就可以作出经过四点的圆，否则不可以。如下图所示。

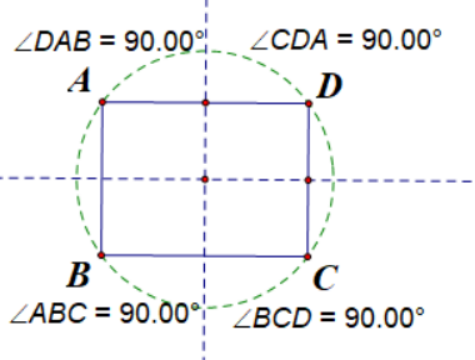
　　得到四点共圆的第一判定命题（证明后是定理）：

　　四条边的垂直平分线相交于一点。

　　证明：如下图，设四边形ABCD的四条边的垂直平分线交于O点，连接OA，OB，OC，OD，

　　∵　O点在AB的垂直平分线上，

　　∴　OA=OB。

　　同理可得

　　OB=OC，OC=OD，

　　∴　OA=OB=OC=OD。

　　∴　A，B，C，D四点在以O点为圆心，OA为半径的圆上。

　　即 A，B，C，D四点共圆。

　　练习题1：我们知道圆内接四边形的性质定理：圆内接四边形对角互补。请提出它的逆命题，然后证明它，作为四点共圆的第二判定定理。

　　活动4：设计图案

　　两条互相垂直的直径把圆弧分为4等份。除此之外，由于60°圆心角所对的弦等于圆的半径，因此也可以用尺规作图法六等分圆弧。一般的与圆有关的图案都与这两个等分有关。

　　用《几何画板》制作下面的图案。

　　制作视频如下。

，时长03:00

　　练习题2：尝试使用《几何画板》完成下面图案的设计。

（1）

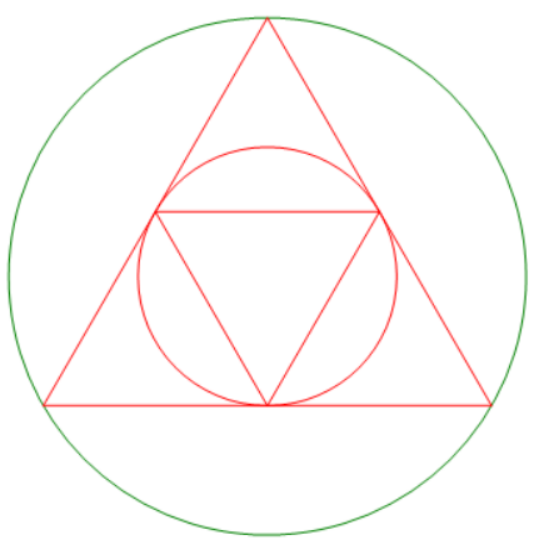
（2）

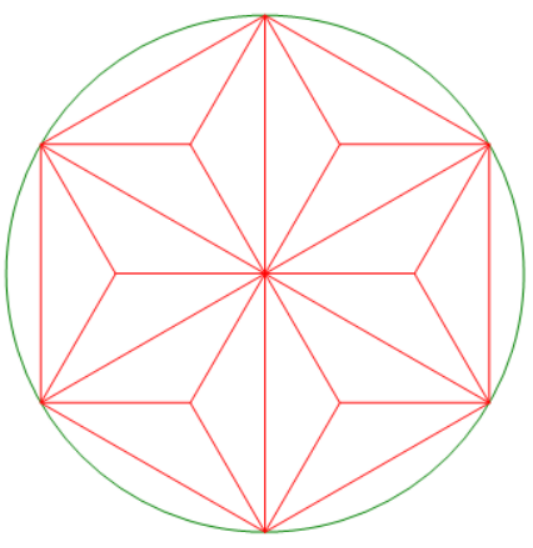
（3）

　　一些正多边形可以密铺整个平面，不过要一个必要条件：这些正多边形的内角可以构成平角或周角，能构成平角的是一些分层的图案，否则是交错型图案。

　　正三角形的内角是60°，3×60°=180°，密铺出分层图案。如下图所示。

　　正四边形的内角是90°，2×90°=180°，也密铺出分层图案。如下图所示。

　　正六边形的内角是120°，3×120°=360°，密铺出交错型图案。如下图所示。

　　除了正三角形、正方形和正六边形可以单独密铺外，没有其它正多边形可以单独密铺了。不过，如果是混合密铺（使用两种正多边形）还可以使用正八边形和正十二边形。

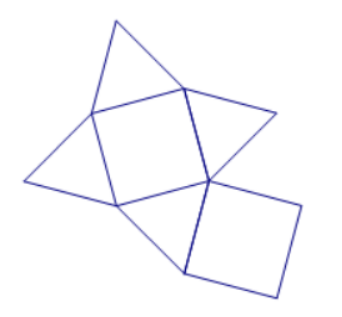
　　采用正三角形和正方形密铺成交错的图案，由于只有2×90°+3×60°=360°，可见每一个交汇点都是由两个正方形顶点和3个正三角形顶点构成，两个正方形不能靠在一起，那么只有一种方案：两个正方形由1个和2个正三角形分隔。一个完整的交汇点如下图所示。

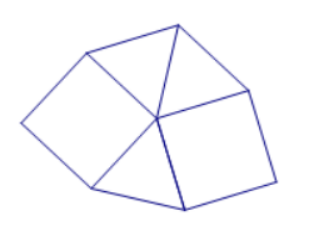
　　密铺时不能使用完整的交汇点，而是使用最小重复单元，如下图所示。

　　用《几何画板》模拟密铺过程的视频如下。

，时长01:02

　　练习题3：尝试使用《几何画板》完成下面图案的设计。

（1）

（2）

　　（3）用正三角形和正十二边形密铺。

　　（4）用不少于两种不同的正多边形，设计不同于上面的一个密铺图案。