在相似多边形中，最简单的就是相似三角形(similar triangles)。如下图，在△ABC和△A'B'C'中，如果

∠A=∠A'，∠B=∠B'，∠C=∠C'，

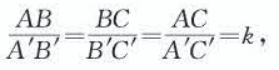
即三个角分别相等，三条边成比例，我们就说△ABC与△A'B'C'相似，相似比为k。相似用符“∽”表示，读作“相似于”。△ABC与△A'B'C'相似记作“△ABC∽△A'B'C'”。

　　思考题：

1、如果△ABC与△A'B'C'的相似比k=1，这两个三角形有什么关系？

2、如果△ABC与△A'B'C'的相似比是k，那么△A'B'C'与△ABC的相似比是多少？

　　判定两个三角形全等时，除了可以验证它们所有的角和边分别相等外，还可以使用简便的判定方法(SSS，SAS，ASA，AAS，HL)。类似地，判定两个三角形相似时，是不是也存在简便的判定方法呢？我们先来探究下面的问题。

　　如下图，任意画两条直线l1，l2，再画三条与l1，12都相交的平行线l3，l4，l5。分别度量l3，l4，l5在l1上截得的两条线段AB，BC和在l2上截得的两条线段DE，EF的长度，AB/BC与DE/EF相等吗？任意平移l5，AB/BC与DE/EF还相等吗？

　　请看下面的视频：

，时长00:45

　　可以发现，当l3//l4//l5时，有AB/BC=DE/EF，BC/AB=EF/DE，AB/AC=DE/DF，BC/AC=EF/DF等。

　　一般地，平行线组分线段成比例的命题（证明后是“平行线组分线段成比例定理”，定理名称是本文自拟的。）：

　　两条直线被一组平行线所截，所得的对应线段成比例。

　　分析：如下图，l1和l2如果平行，所截的对应线段相等，自然成比例，如果不平行，过l1和l3交点，作l2的平行线，转化为三角形中的线比例问题。根据同底平行线之间的三角形面积相等，等高面积比等于底边之比得证。证法参考《几何原本》。

　　证明：分l1和l2平行和不平行两种情况。

　　（1）l1和l2平行，如下图。

　　∵　l1//l2，l3//l4//l5，

　　∴　AB=DE，BC=EF，AC=DF，

　　∴　AB/BC=DE/EF，BC/AB=EF/DE，

　　　　AB/AC=DE/DF，BC/AC=EF/DF。

　　（2）l1和l2不平行，如下图，过A点作l2的平行线交l4于E'，交l5于F'，连接BF'和CE'。

　　∵　l4//l5，

　　∴　S△BE'C=S△E'BF'，

　　∴　S△BE'C/S△ABE'=S△E'BF'/S△ABE'，

　　又　∵　△BEC与△ABE'的高相同，　

　　∴　S△BE'C/S△ABE'=BC/AB，

　　同理得

 　　S△E'BF'/S△ABE'=E'F'/AE'，

　　∴　BC/AB=E'F'/AE'。

　　又　∵　E'F'//l2，

　　∴　E'F'=EF，AE'=DE，

　　∴　BC/AB=EF/DE。

　　等式两边的比前后项对调得

　　AB/BC=DE/EF。

　　同理得，

　　AB/AC=DE/DF，BC/AC=EF/DF。

　　把三角形的一底边看成一组平行线中的一条，过它对应的顶点作另外一条平行于这底边的平行线，第三条平行线会出现下面两种情况。

　　对于第二条平行线（l3），第三条平行线（l4）与第一条平行线（l5）同一侧，如下图。

　　对于第二条平行线（l4），第三条平行线（l3）与第一条平行线（l5）不同侧，如下图。

　　因此，对于三角形，上面的定理可以陈述为“三角形平行底定理”（定理名称是本文自拟的）：

　　平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例。

　　上面定理的逆命题（证明后是定理）：

　　如果一条直线截三角形两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形第三边。

　　如下图，直线l交△ABC的AB和AC（或BA，CA的延长线）于D和E，AD/AB=AE/AC，求证：l//BC。

　　分析：原命题已证明是真命题，那么逆命题适合使用反证法。假设l与BC不平行，过D点作BC的平行线，与AC的交点也是E得证。

　　证明：如下图，假设l与BC不平行，过D点作BC的平行线l'，与AC的交于E'，过A点作BC的平行线l''，

　　∴　AD/AB=AE'/AC，

　　又　AD/AB=AE/AC，

　　∴　AE=AE'，

　　又　如果D在AB上，那么E也在AC上；如果D在BA延长线上，　那么E也在CA延长线上，即D，E在直线l''的同一侧。

　　∵　l'//BC，l''//BC，

　　∴　l'//l''。

　　∴　D，E'在直线l''的同一侧。

　　∴　E和E'重叠。

　　∵　两点决定一条直线，

　　∴　l和l'是同一条直线，与假设l与BC不平行相矛盾，

　　∴　l//BC。

　　如下图，在△ABC中，DE//BC，且DE分别交AB，AC于点D，E，△ADE与△ABC有什么关系？

　　请看下面的视频。

，时长00:29

　　从视频中，我们容易看出，△ADE与△ABC相似。

　　分析：∠A为公共角，其它两个角由平行线性质可知相等，由上面的定理可得AD/AB=AE/AC，因此只要证明DE/BC=AD/AB或DE/BC=AE/AC就行。DE不在BC上，不能应用上面的定理，因此需要把DE投影到BC上，同理得证。

　　证明：先证明两个三角形的角分别相等。

　　如下图，在△ADE与△ABC中，∠A=∠A，

　　∵　DE//BC，

　　∴　∠ADE=∠B，∠AED=∠C。

　　再证明两个三角形的边成比例。

　　过点E作EF//AB，交BC于点F。

　　∵　DE//BC，EF//AB，

　　∴　AD/AB=AE/AC，BF/BC=AE/AC，

　　∵　四边形DBFE是平行四边形，

　　∴　DE=BF。

　　∴　DE/BC=AE/AC。

　　∴　AD/AB=AE/AC=DE/BC。

　　∴　△ADE∽△ABC。

　　因此，我们有如下判定三角形相似的基础定理：

　　平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似。

　　练习题1：

3.　如下图，四边形ABCD，AD//BC，E，F分别是AB和CD上的一点，AE/EB=DF/FC，求证：EF//BC。