使用decimal的通常方式是先创建Decimal实例，然后用它们进行算术运算，这些运算发生在活动线程的当前上下文中。一种替代方式是直接使用特定的上下文的方法进行计算。这些方法类似于Decimal的实例方法，在此仅简单地重新列出。
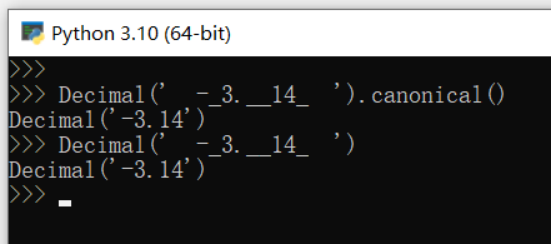
canonical(x) 返回相同的 Decimal 对象 x。 x.canonical() 返回Decimal对象的规范编码。目前，一个Decimal对象的编码始终是规范的（输入不规范时，在输入过程中已经消除。），因此该操作返回与直接打印相同。
compare(x, y) 对 x 与 y 进行数值比较。this：当前上下文对象。 x.compare(y,context=this) 比较两个Decimal对象的值。compare()返回一个Decimal对象，如果任一操作数是NaN，那么结果是NaN；如果任一操作是sNaN（显式NaN），那么抛出异常InvalidOperation。context参数似乎没有什么作用，因为它只对运算结果进行有效数字舍入。
compare_signal(x, y) 对两个操作数进行数值比较。 x.compare_signal(y, context=this) 与x.compare(y, context=this)基本一样，不过对于有一个参数是NaN的情况不是返回Decimal('NaN')，而是抛出信号，如果设置了相应的陷阱，就会抛出异常InvalidOperation。
compare_total(x, y) 对两个操作数使用其抽象表示进行比较。 x.compare_total(y, context=this)
使用两个操作数的抽象表示（可以认为是DecimalTuple）而不是它们的数值来比较。类似于compare()方法，不过是对全部项目的综合排序而得到结果（Decimal对象）。两个具有相同的数值但有效数字个数不同的Decimal对象比较，结果不相等。例如：
>>> Decimal('12.0').compare_total(Decimal('12'))
Decimal('-1')
下面是不考虑NaN和Infinity的算法（文本代码附录1）和运行结果：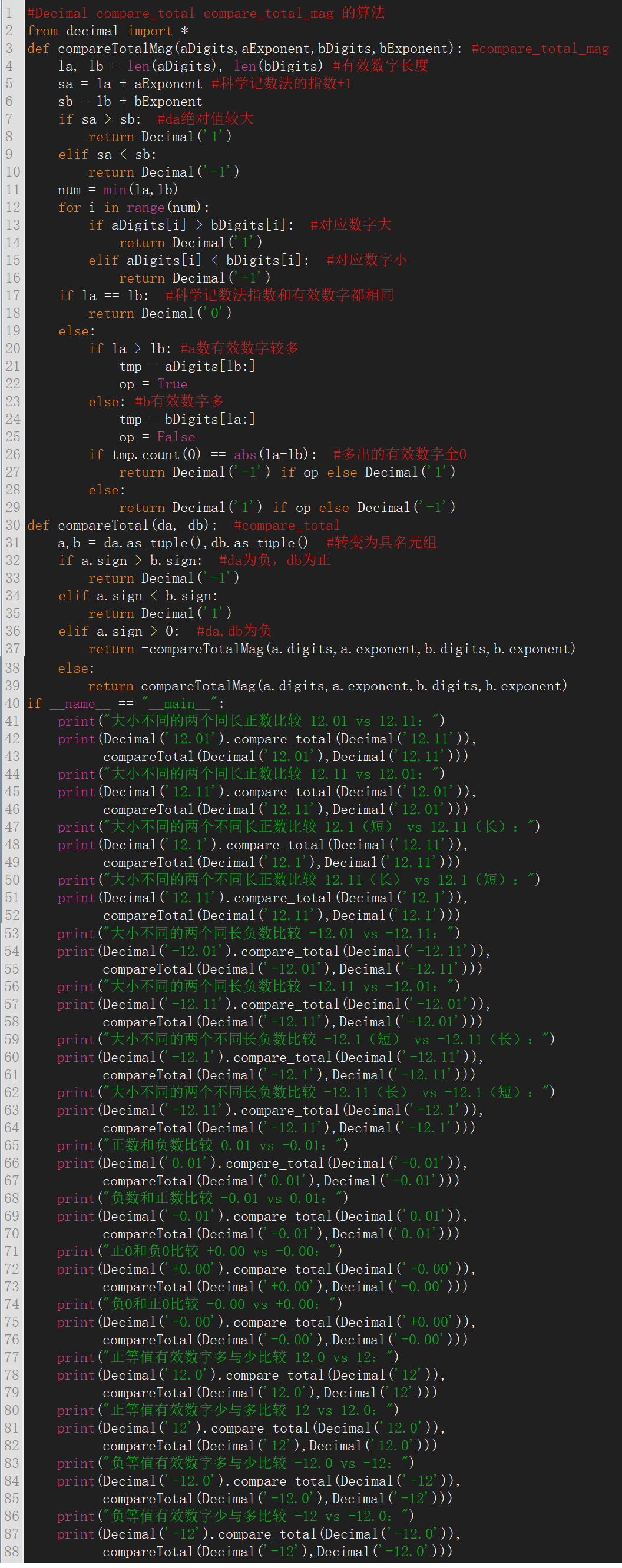
静默NaN（NaN）和显式NaN（sNaN）也可以排序：
。可见它们的排序是NaN>sNaN>数字或±Infinity。 如果两个操作数综合排序相同返回 Decimal('0')；如果第一个操作数的综合排序低于第二个操作返回Decimal('-1')；如果第一个操作数在综合排序高于第二个操作数返回Decimal('1')。 这个方法不受上下文影响且静默：不更改任何标志且不执行舍入。不过，如果底层的C语言程序无法准确转换第二个操作数，可能会引发InvalidOperation异常。
compare_total_mag(x, y) 对两个操作数使用其抽象表示进行比较，忽略符号。 x.compare_total_mag(y, context=this) 这个方法与compare_total()相似，但忽略每个操作数的符号（即只比较绝对值）。x.compare_total_mag(y) 相当于 x.copy_abs().compare_total(y.copy_abs())。
这个方法不受上下文影响且静默：不更改任何标志且不执行舍入。不过，如果底层的C语言程序无法准确转换第二个操作数，可能会引发InvalidOperation异常。
copy_abs(x) 返回 x 的副本，符号设为 0。 x.copy_abs() 返回对象的绝对值。这个方法不受上下文影响且静默：不更改任何标志且不执行舍入。
copy_negate(x) 返回 x 的副本，符号取反。 x.copy_negate() 返回对象的取反值。这个方法不受上下文影响且静默：不更改任何标志且不执行舍入。
copy_sign(x, y) 从 y 拷贝符号至 x。 x.copy_sign(y, context=this) 返回第一个操作数的副本，并把它的符号设置为第二个操作数的符号。
这个方法不受上下文影响且静默：不更改任何标志且不执行舍入。不过，如果底层的C语言程序无法准确转换第二个操作数，可能会引发InvalidOperation异常。
exp(x) Returns e ** x. x.exp(context=this) 返回该数字的（自然）指数函数“e**x”的值。结果使用 ROUND_HALF_EVEN 舍入模式舍入。
fma(x, y, z) 返回 x 乘以 y 再加 z 的结果。 x.fma(y,z, context=this) 混合乘法与加法。返回 x*y+z 值，中间乘积 x*y 没有舍入。
is_canonical(x) 如果 x 是规范的则返回 True；否则返回 False。 x.is_canonical() 如果参数是规范的，则为返回 True，否则为 False 。目前，Decimal实例总是规范的，所以这个操作总是返回 True 。
is_finite(x) 如果 x 为有限的则返回``True``；否则返回 False。 x.is_finite() 如果参数是一个有限的数，则返回为 True ；如果参数为无穷大或 NaN ，则返回为 False。
is_infinite(x) 如果 x 是无限的则返回 True；否则返回 False。 x.is_infinite() 如果参数为正负无穷大，则返回为 True ，否则为 False 。
is_nan(x) 如果 x 是 qNaN 或 sNaN 则返回 True；否则返回 False。 x.is_nan() 如果参数为 NaN （无论是否静默），则返回为 True ，否则为 False 。
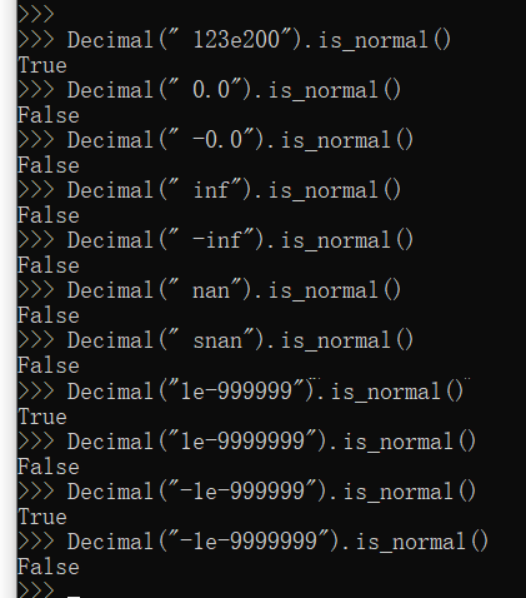
is_normal(x) 如果 x 是标准数则返回 True；否则返回 False。 x.is_normal(context=this) 如果参数是一个标准的有限数则返回True。如果参数为零、次标准数（绝对值过小的数值，默认上下文可能是不大于10^-9999999的数）、无穷大或NaN则返回False。
is_qnan(x) 如果 x 是静默 NaN 则返回 True；否则返回 False。 x.is_qnan() 如果参数为静默 NaN，返回 True，否则返回 False。
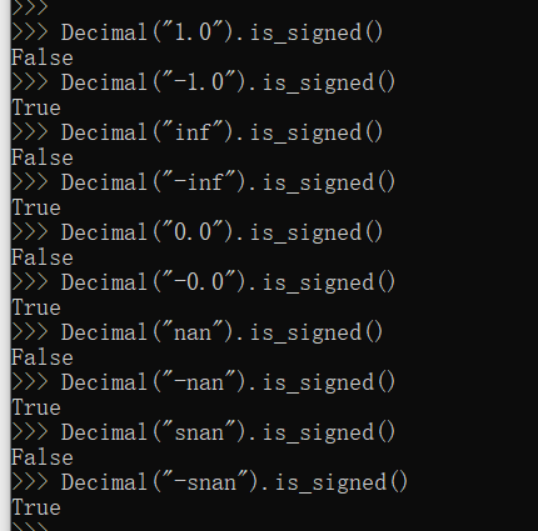
is_signed(x) x 是负数则返回 True；否则返回 False。 x.is_signed() 如果参数带有负号，则返回为True，否则返回False。注意，0和NaN都可带有符号。
is_snan(x) 如果 x 是显式 NaN 则返回 True；否则返回 False。 x.is_snan() 如果参数为显式NaN，则返回True，否则返回 False。
is_subnormal(x) 如果 x 是次标准数则返回 True；否则返回 False。 x.is_subnormal(context=this) 如果参数为次标准数，则返回True，否则返回 False。
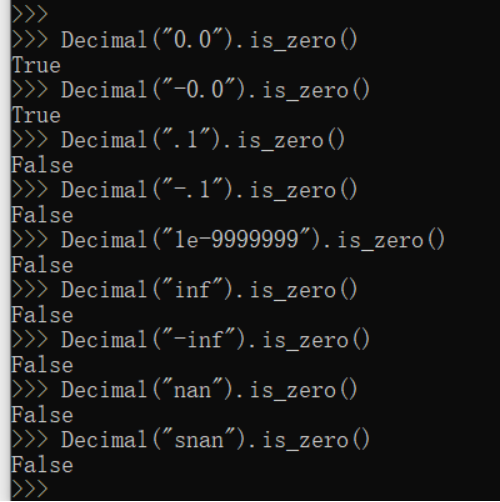
is_zero(x) 如果 x 为零则返回 True；否则返回 False。 x.is_zero() 如果参数是0（正负皆可），则返回 True，否则返回 False。
ln(x) 返回 x 的自然对数（以 e 为底）。 x.ln(context=this) 返回操作数的自然对数（以 e 为底）。结果是使用 ROUND_HALF_EVEN 舍入模式舍入。
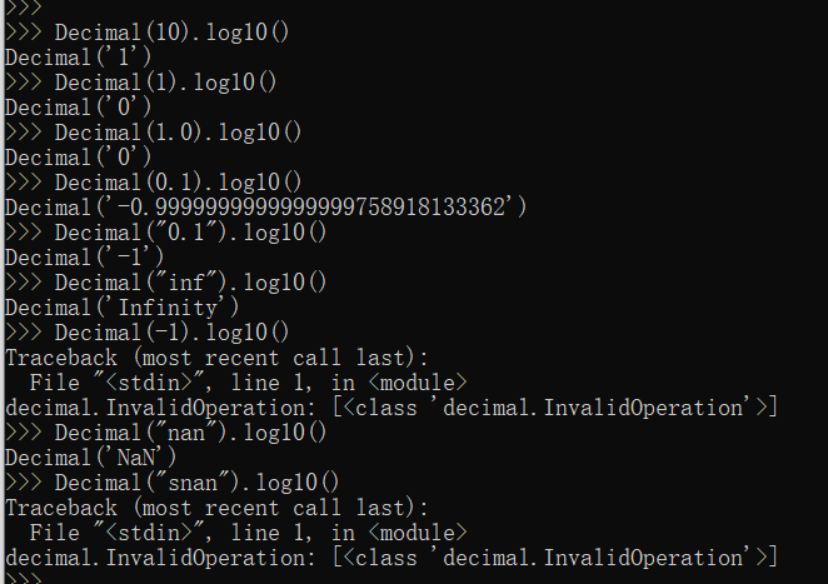
log10(x) 返回 x 的以 10 为底的对数。 x.log10(context=this) 返回操作数的以十为底的对数。结果是使用 ROUND_HALF_EVEN 舍入模式舍入。
logb(x) 返回操作数的 MSD 等级的指数。 x.logb(context=this) 对于一个非零数（特别是浮点数），在做log10运算前调整生成一个与原十进制相符的副本，以这个副本做log10()运算得到一个Decimal实例的结果。与log10()一样，如果操作数是无限大则返回Decimal('Infinity') 。与log10()不同，如果操作数为零将抛出DivisionByZero异常。
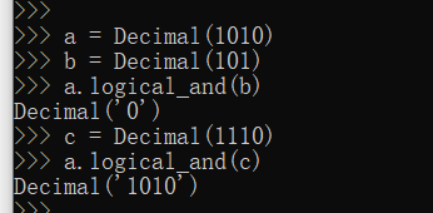
logical_and(x, y) 在操作数的每个数位间应用逻辑运算 and。 x.logical_and(y,context=this) 按位“与”运算。两个操作数均为逻辑精确数（符号和指数都为0，系数是0和1组成的十进制数，下面三个方法的操作数也同样。）。
logical_invert(x) 取反 x 中的所有数位。 x.logical_invert(context=this) 按位“取反”运算。
logical_or(x, y) 在操作数的每个数位间应用逻辑运算 or。 x.logical_or(y,context=this) 按位“或”运算。
logical_xor(x, y) 在操作数的每个数位间应用逻辑运算 xor。 x.logical_xor(y,context=this) 按位“异或”运算。
max(x, y) 对两个值执行数值比较并返回其中的最大值。 x.max(y,context=this) 与内置函数max(x, y) 一样求两个数的最大值。该方法提供用户输入的Context舍入规则对返回结果进行舍入和用信号抛出规则。
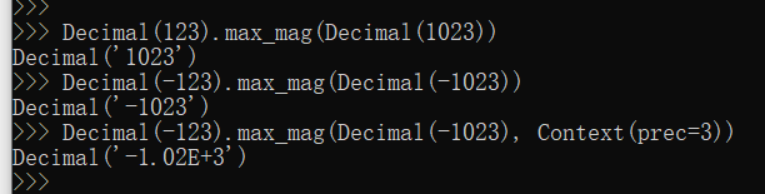
max_mag(x, y) 对两个值执行忽略正负号的数字比较。 x.max_mag(y,context=this) 与max()方法相似，不过是用操作数的绝对值进行比较的。
min(x, y) 对两个值执行数字比较并返回其中的最小值。 x.min(y,context=this) 与max()方法相似，求两个操作数的最小值。
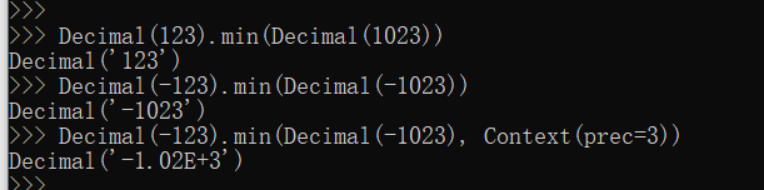
min_mag(x, y) 对两个值执行忽略正负号的数字比较。 x.min_mag(y,context=this) 与max_mag()方法相似，求两个操作数的最小值。
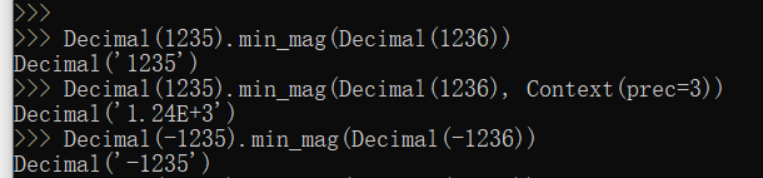
next_minus(x) 返回小于 x 的最大数字表示形式。 x.next_minus(context=this) 如果输入上下文参数（context），则运算上下文采用这个参数，否则采用运行环境上下文；方法返回该数的左靠近数——小于该操作数并符合上下文规定的最大数字。
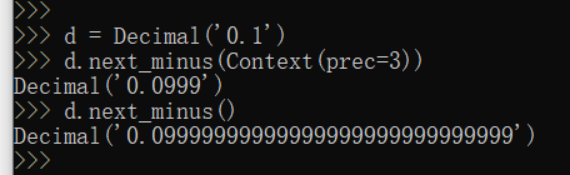
next_plus(x) 返回大于 x 的最小数字表示形式。 x.next_plus(context=this) 与next_minus()相似，返回右靠近值。
next_toward(x, y) 返回 x 趋向于 y 的最接近的数字。 x.next_toward(y, context=this) 如果两运算数不相等，返回在第二个操作数的方向上最接近第一个操作数的数。如果两操作数数值上相等，返回将符号设置为与第二个运算数相同的第一个运算数的拷贝。
normalize(x) 将 x 改写为最简形式。 x.normalize(context=this) 标准化数字。通过去除尾随的零，并将所有结果等于Decimal('0')或Decimal('-0') 的分别转化为Decimal('0')或Decimal('-0') 。用于为一类等值的数生成同样的规范表示。比如， Decimal('32.100') 和 Decimal('0.321000e+2') 都被标准化为相同的值 Decimal('32.1')。
number_class(x) 返回 x 的类的表示。 x.number_class(context=this) 返回操作数的类别，是以下十个字符串中的一个："-Infinity" ，指示运算数为负无穷大。"-Normal" ，指示该运算数是负正常数字。"-Subnormal" ，指示该运算数是负的次标准数。"-Zero" ，指示该运算数是负零。"+Zero" ，指示该运算数是正零。"+Subnormal" ，指示该运算数是正的次标准数。"+Normal" ，指示该运算数是正的标准数。"+Infinity" ，指示该运算数是正无穷。"NaN" ，指示该运算数是肃静 NaN （非数字）。"sNaN" ，指示该运算数是信号 NaN 。
quantize(x, y) 返回的值等于 x (舍入后)，并且指数为 y。 x.quantize(y, rounding=None, context=this) 把第二个操作数（exp）通过小数点移位变成等值的整数和指数（左移一位指数加1，右移一位指数减1），然后也通过小数点移位的方式，使第一个操作数（对象本身）的指数与移位后的第二个操作数的指数相同，然后按rounding参数或上下文的舍入模式去除小数点后的数字即得结果。如果第一操作数的小数点右移位时，位数不够则补0。 例1：精确数1.41421356×10^2进行1.000×10^-1的quantize运算，首先把1.000×10^-1中系数的小数点等值后移3位变成1000×10^-4，然后把1.41421356×10^2等值变换为指数是-4的数，即右移6位变成1414213.56×10^-4，最后把系数四舍五入为整数即1414214×10^-4，用纯小数表示就是141.4214。
例2：精确数1.41421356×10^2进行1.000×10^7的quantize运算，首先把1.000×10^7中系数的小数点等值后移3位变成1000×10^4，然后把1.41421356×10^2等值变换为指数是4的数，即左移2位变成0.0141421356×10^4，最后把系数四舍五入为整数即0×10^4。
例3：精确数1.41421356×10^2进行1.000×10^-9的quantize运算，首先把1.000×10^-9中系数的小数点等值后移3位变成1000×10^-12，然后把1.41421356×10^2等值变换为指数是-12的数，即右移14位变成141421356000000×10^-12，无需舍入操作，用纯小数表示就是141.421356000000。
第四个参数由于可以限制有效数字的多少，可能会与quantize运算有冲突。与其他运算不同，如果按要求舍入后系数的有效数字超过上下文的限制，就会发出一个 InvalidOperation信号。
第三个操作数是舍入方式。如果两个操作数等值移位后，第一个操作数还有小数位，就需要舍入操作。在这种情况下，舍入模式由给定 rounding 参数决定，其余的由给定 context 参数决定；如果参数都未给定，使用当前线程上下文的舍入模式。
每当结果的指数大于 Emax 或小于 Emin 就会返回错误。
radix() 恰好返回10，因为这是Decimal对象。 Decimal(?).radix()
返回 Decimal(10)，即 Decimal 类进行所有算术运算所用的数制（基数）。这是为保持与规范描述的兼容性而加入的。
remainder_near(x, y) 返回 x - y * n，其中 n 为最接近 x / y 实际值的整数（如结果为 0 则其符号将与 x 的符号相同）。 x.remainder_near(y, context=this) 返回x除以y的最近余数。这与 x % y 的区别在于所选择的余数要使其绝对值最小。更准确地说，返回值为 x - n * y 其中 n 是最接近 x / y 的实际值的整数，并且如果两个整数与实际值的差相等则会选择其中的偶数。如果结果为零则其符号将为 x 的符号。
rotate(x, y) 返回 x 翻转 y 次的副本。 x.rotate(y, context=this) 返回对第一个操作数的系数（digits）按第二个操作数所指定的数量进行轮转的结果。第二个操作数必须为 -precision 至 precision 精度范围内的整数。第二个操作数的绝对值给出要轮转的位数。如果第二个操作数为正值则向左轮转；否则向右轮转。如有必要第一个操作数的系数会在左侧填充零以达到 precision 所指定的长度。第一个操作数的符号和指数保持不变。
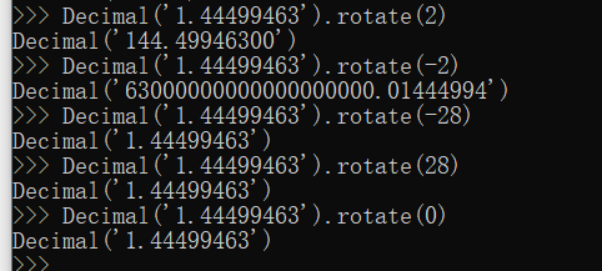
same_quantum(x, y) 如果两个操作数具有相同的指数则返回 True。 x.same_quantum(y, context=this) 检测自身与 y 是否具有相同的指数或是否均为 NaN。
此操作不受上下文影响且静默：不更改任何标志且不执行舍入。但是，如果无法准确转换第二个操作数，则C语言底层可能会引发InvalidOperation异常。
scaleb(x, y) 返回第一个操作数添加第二个值的指数后的结果。 x.scaleb(y, context=this) 小数点移位操作。返回第一个操作数的指数加第二个操作数进行调整的结果。等价于返回第一个操作数乘以 10**y 的结果。第二个操作数必须为整数。
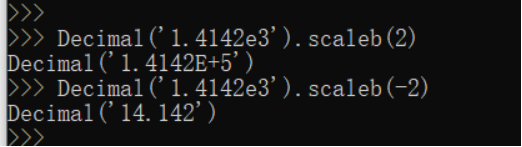
shift(x, y) 返回 x 变换 y 次的副本。 x.shift(y, context=this) 返回第一个操作数的系数（digits）按第二个操作数所指定的数量进行移位的结果。第二个操作数必须为 -precision 至 precision 范围内的整数。第二个操作数的绝对值给出要移动的位数。如果第二个操作数为正值则向左移位；否则向右移位；小数点位置不变。移入系数的数码为零。第一个操作数的符号和指数保持不变。
注：1.4142向右移动2位，小数点位置不变，则成了0.0141，指数不变得结果0.0141×10^3，即14.1。
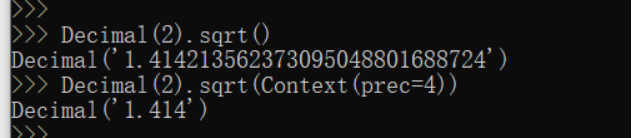
sqrt(x) 非负数基于上下文精度的平方根。 x.sqrt(context=this) 返回参数的平方根精确到完整精度。
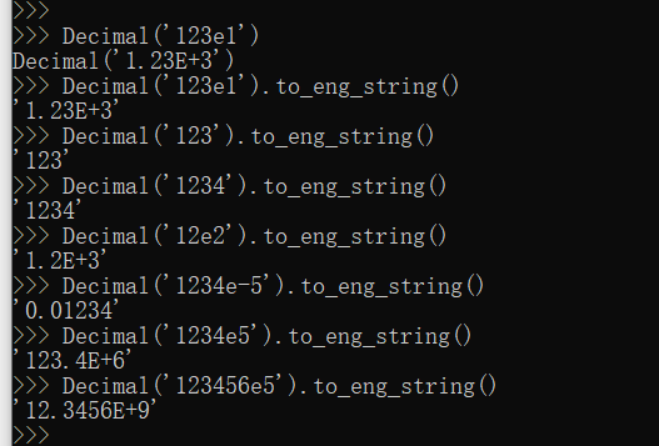
to_eng_string(x) 转换为字符串，如果需要指数则会使用工程标注法。 工程标注法的指数是 3 的倍数。这会在十进制位的左边保留至多 3 个数码，并可能要求添加一至两个末尾零。 x.to_eng_string(context=this) 转换为字符串，如果需要指数则使用工程标注法。 工程标注法的指数是 3 的倍数。这会在十进制位的小数点左边保留至多 3 个数码，并可能要求添加一至两个末尾零。
to_integral(x) 舍入到一个整数。 x.to_integral(rounding=None, context=this) 与 to_integral_value() 方法（后面）相同。保留 to_integral 名称是为了与旧版本兼容。
to_integral_exact(x) 舍入到一个整数。 x.to_integral_exact(rounding=None, context=this) 舍入到最接近的整数，发出信号 Inexact 或者如果发生舍入则相应地发出信号 Rounded。如果给出 rounding 形参则由其确定舍入模式，否则由给定的 context 来确定。如果没有给定任何形参则会使用当前上下文的舍入模式。
to_integral_value(x) 静默转整数。 x.to_integral_value(rounding=None, context=this) 舍入到最接近的整数而不发出 Inexact 或 Rounded 信号。如果给出 rounding 则会应用其所指定的舍入模式；否则使用所提供的 context 或当前上下文的舍入方法。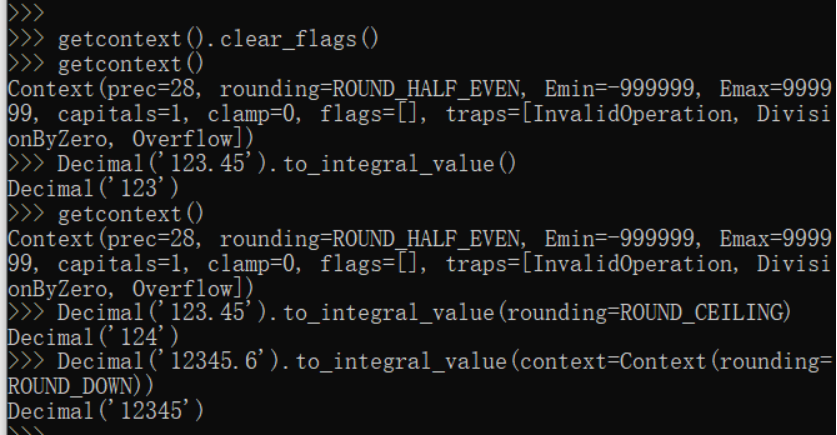
附录1：
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
#Decimal compare_total compare_total_mag 的算法from decimal import *def compareTotalMag(aDigits,aExponent,bDigits,bExponent): #compare_total_mag la, lb = len(aDigits), len(bDigits) #有效数字长度 sa = la + aExponent #科学记数法的指数+1 sb = lb + bExponent if sa > sb: #da绝对值较大 return Decimal('1') elif sa < sb: return Decimal('-1') num = min(la,lb) for i in range(num): if aDigits[i] > bDigits[i]: #对应数字大 return Decimal('1') elif aDigits[i] < bDigits[i]: #对应数字小 return Decimal('-1') if la == lb: #科学记数法指数和有效数字都相同 return Decimal('0') else: if la > lb: #a数有效数字较多 tmp = aDigits[lb:] op = True else: #b有效数字多 tmp = bDigits[la:] op = False if tmp.count(0) == abs(la-lb): #多出的有效数字全0 return Decimal('-1') if op else Decimal('1') else: return Decimal('1') if op else Decimal('-1') def compareTotal(da, db): #compare_total a,b = da.as_tuple(),db.as_tuple() #转变为具名元组 if a.sign > b.sign: #da为负，db为正 return Decimal('-1') elif a.sign < b.sign: return Decimal('1') elif a.sign > 0: #da,db为负 return -compareTotalMag(a.digits,a.exponent,b.digits,b.exponent) else: return compareTotalMag(a.digits,a.exponent,b.digits,b.exponent) if __name__ == "__main__": print("大小不同的两个同长正数比较 12.01 vs 12.11：") print(Decimal('12.01').compare_total(Decimal('12.11')), compareTotal(Decimal('12.01'),Decimal('12.11'))) print("大小不同的两个同长正数比较 12.11 vs 12.01：") print(Decimal('12.11').compare_total(Decimal('12.01')), compareTotal(Decimal('12.11'),Decimal('12.01'))) print("大小不同的两个不同长正数比较 12.1（短） vs 12.11（长）：") print(Decimal('12.1').compare_total(Decimal('12.11')), compareTotal(Decimal('12.1'),Decimal('12.11'))) print("大小不同的两个不同长正数比较 12.11（长） vs 12.1（短）：") print(Decimal('12.11').compare_total(Decimal('12.1')), compareTotal(Decimal('12.11'),Decimal('12.1'))) print("大小不同的两个同长负数比较 -12.01 vs -12.11：") print(Decimal('-12.01').compare_total(Decimal('-12.11')), compareTotal(Decimal('-12.01'),Decimal('-12.11'))) print("大小不同的两个同长负数比较 -12.11 vs -12.01：") print(Decimal('-12.11').compare_total(Decimal('-12.01')), compareTotal(Decimal('-12.11'),Decimal('-12.01'))) print("大小不同的两个不同长负数比较 -12.1（短） vs -12.11（长）：") print(Decimal('-12.1').compare_total(Decimal('-12.11')), compareTotal(Decimal('-12.1'),Decimal('-12.11'))) print("大小不同的两个不同长负数比较 -12.11（长） vs -12.1（短）：") print(Decimal('-12.11').compare_total(Decimal('-12.1')), compareTotal(Decimal('-12.11'),Decimal('-12.1'))) print("正数和负数比较 0.01 vs -0.01：") print(Decimal('0.01').compare_total(Decimal('-0.01')), compareTotal(Decimal('0.01'),Decimal('-0.01'))) print("负数和正数比较 -0.01 vs 0.01：") print(Decimal('-0.01').compare_total(Decimal('0.01')), compareTotal(Decimal('-0.01'),Decimal('0.01'))) print("正0和负0比较 +0.00 vs -0.00：") print(Decimal('+0.00').compare_total(Decimal('-0.00')), compareTotal(Decimal('+0.00'),Decimal('-0.00'))) print("负0和正0比较 -0.00 vs +0.00：") print(Decimal('-0.00').compare_total(Decimal('+0.00')), compareTotal(Decimal('-0.00'),Decimal('+0.00'))) print("正等值有效数字多与少比较 12.0 vs 12：") print(Decimal('12.0').compare_total(Decimal('12')), compareTotal(Decimal('12.0'),Decimal('12'))) print("正等值有效数字少与多比较 12 vs 12.0：") print(Decimal('12').compare_total(Decimal('12.0')), compareTotal(Decimal('12'),Decimal('12.0'))) print("负等值有效数字多与少比较 -12.0 vs -12：") print(Decimal('-12.0').compare_total(Decimal('-12')), compareTotal(Decimal('-12.0'),Decimal('-12'))) print("负等值有效数字少与多比较 -12 vs -12.0：") print(Decimal('-12').compare_total(Decimal('-12.0')), compareTotal(Decimal('-12'),Decimal('-12.0')))