statistics.quantiles(data, *, n=4, method='exclusive') 将 data 分隔为具有相等概率的 n 个连续区间。返回分隔这些区间的 n - 1 个分隔点的列表。特殊参数（*）后的形参只能用关键字输入。 将n设为4，则分4个相等的区间（默认值）。
将n设为6，则分6个相等的区间。
如果n=1，这函数不需要干什么，直接返回空列表。
如果n<1，则将引发StatisticsError。
如果数据项的个数小于2则将引发StatisticsError。
分隔点是通过对两个最接近的数据项进行线性插值得到的。插值方法与method参数有关。method参数可取2个值：exclusive（不包括，默认值）和inclusive（包括）。当method='exclusive'时（默认），采用正比例插值，即左右长度比等于左右段数比；当method='inclusive'时，采用反比例插值，即左右长度比等于右左段数比： p=p1+(p2-p1)×(m/n) （method='exclusive'）， ①
p=p1+(p2-p1)×[(n-m)/n] （method='inclusive'）， ② p是插值点， p1是低点， p2是高点， m是第几个插入点（1开始）， n是分段数。 把[1,2,3,4,5,6,7,8,9,10,11,12]分四段，代入上面的公式，得到结果：[3.25, 6.5, 9.75] （method='exclusive'），[3.75, 6.5, 9.25] （method='inclusive'）。
验证：
把②式变换一下就变成： p=p2 - (p2-p1)×(m/n)，也就是说，当method='inclusive'时，分割点是从右点往左走正比例的长度。 data可以是包含样本数据的任意可迭代对象。为了获得有意义的结果，data中数据项的数量应当大于n。
至于采用哪种method，由输入的数据data是包含（includes）还是排除（excludes）总体的最低和最高可能值而定。包含（includes）用method='inclusive'；排除（excludes）用method='exclusive'。 当总体数据中能找到比样品数据中最小值更小、或比样品数据中最大值更大的数据项时，采用method='exclusive'。对于一个已经排好序的m个数据项的序列，第i个数据项（从1开始）的积累概率：SP=i/(m+1)。（i从1开始）
比如，九个已排好序的样本数据：[1,2,4,8,16,32,64,128,256]，根据上面的公式，可以计算出各个数据项对应的概率（百分数）：
[10%,20%,30%,40%,50%,60%,70%,80%,90%]。
可见，最后一个数据项的积累概率不是100%。
当样品数据中已包含总体的最大最小值，采用method='inclusive'。数据中的最小值的积累概率被认为是0，而最大值是1。对于一个已经排好序的m个数据项的序列，第i个数据项（从1开始）的积累概率：SP=(i-1)/(m-1)。（i从1开始）比如，11个已排好序的样本数据：[1,2,4,8,16,32,64,128,256,512,1024]，根据上面的公式，可以计算出各个数据项对应的概率（百分数）：
[0%,10%,20%,30%,40%,50%,60%,70%,80%,90%,100%]。
可见，最后一个数据项的积累概率是100%。 不管哪一种，最后还是用最后一个数据项的积累概率为等分总概率。 最后，用官方文档上的数据，进行quantiles函数的模拟测试，代码（文本代码附录1）和运行结果如下：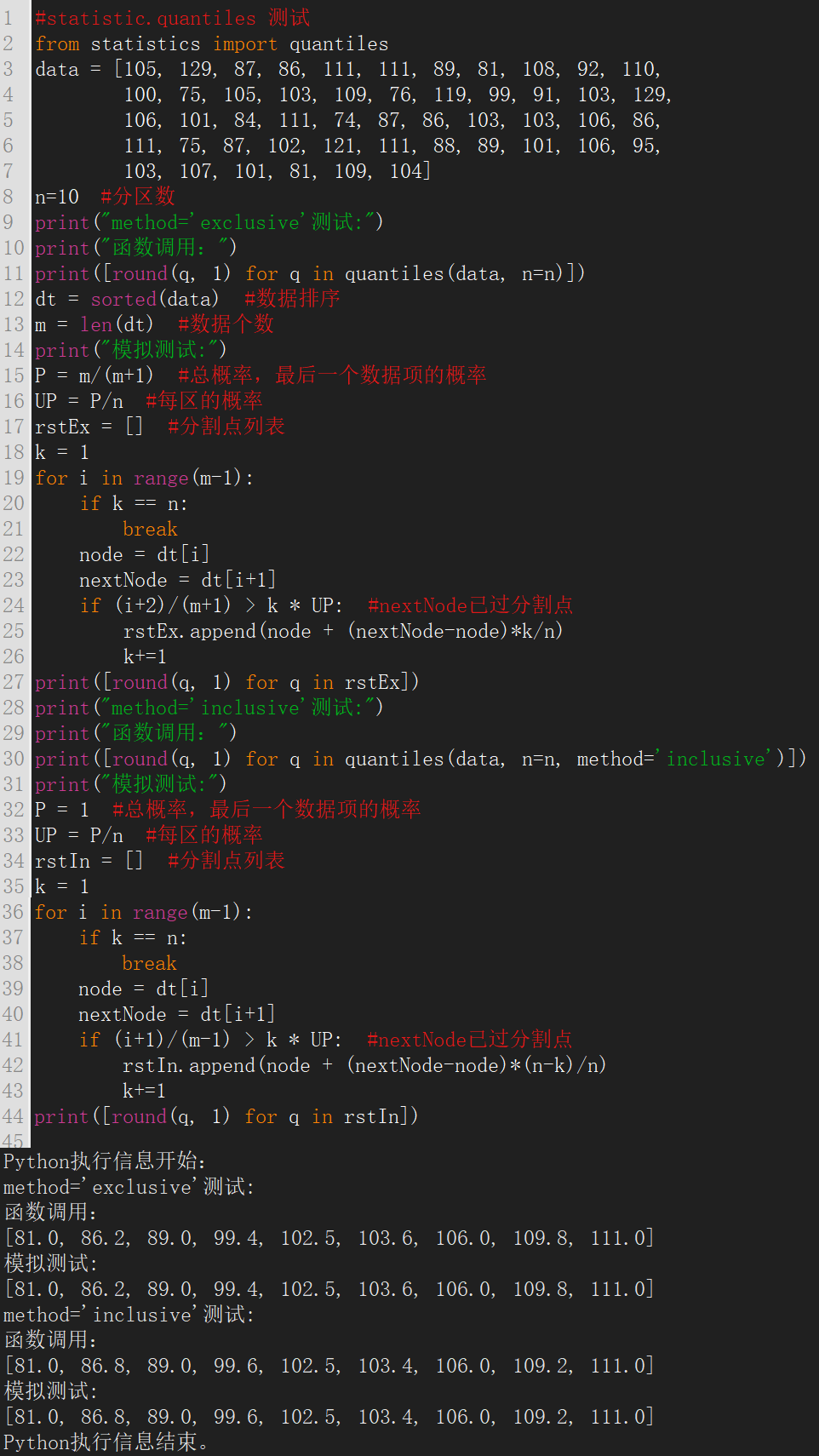
可见，文中对quantiles函数的算法描述完全正确。
附录1：
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
#statistic.quantiles 测试from statistics import quantilesdata = [105, 129, 87, 86, 111, 111, 89, 81, 108, 92, 110, 100, 75, 105, 103, 109, 76, 119, 99, 91, 103, 129, 106, 101, 84, 111, 74, 87, 86, 103, 103, 106, 86, 111, 75, 87, 102, 121, 111, 88, 89, 101, 106, 95, 103, 107, 101, 81, 109, 104] n=10 #分区数print("method='exclusive'测试:")print("函数调用：")print([round(q, 1) for q in quantiles(data, n=n)]) dt = sorted(data) #数据排序m = len(dt) #数据个数print("模拟测试:")P = m/(m+1) #总概率，最后一个数据项的概率UP = P/n #每区的概率rstEx = [] #分割点列表k = 1for i in range(m-1): if k == n: break node = dt[i] nextNode = dt[i+1] if (i+2)/(m+1) > k * UP: #nextNode已过分割点 rstEx.append(node + (nextNode-node)*k/n) k+=1print([round(q, 1) for q in rstEx])print("method='inclusive'测试:")print("函数调用：")print([round(q, 1) for q in quantiles(data, n=n, method='inclusive')]) print("模拟测试:")P = 1 #总概率，最后一个数据项的概率UP = P/n #每区的概率rstIn = [] #分割点列表k = 1for i in range(m-1): if k == n: break node = dt[i] nextNode = dt[i+1] if (i+1)/(m-1) > k * UP: #nextNode已过分割点 rstIn.append(node + (nextNode-node)*(n-k)/n) k+=1print([round(q, 1) for q in rstIn])