
绝对值是点到原点的距离,非负数。复数相当于平面直角坐标系中的一点,复数绝对值(复数的轭)是实数部分与虚数部分系数平方和的算术平方根。本题答案B. 2。

数的整数幂是底数的指数个相乘,2²=2×2=4。本题答案:D. 4。

长方形和正方形都是矩形,矩形属于平行四边形,所以长方形和正方形都是平行四边形,但平行四边形不稳定,三角形具有稳定性,答案:A。

平行线同位角相等,所以∠2=∠1=40°,答案:B。

三角形中位线平行于底并是底的一半=4/2=2,答案:D。

从左到右是x轴的正向,向右平移2个单位,即x坐标增加2,即(3,1),答案:A。

概率是样本占总体的比值,样本数是1,总体是3本书每次取一本,共3次,概率是1:3,答案:B。

平行四边形对边平行并相等,在所有选项中,只有AB=CD一定正确,答案:C。

反比例函数x坐标与y坐标乘积恒等,所以x坐标越大y坐标越小,最小y4,答案:D。

变量是过程中不断改变大小,2和π是不变的,r、C是变量,答案:C。

有一锐角30°的直角三角形,斜边2,对边1,邻边√3(根号3),所以sin30°=½。
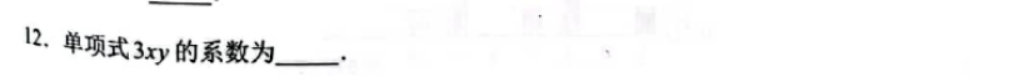
系数是单项式中的常量,答案:3 。

菱形的四边相等,周长=5×4=20。

方程的根是使方程成立的变量值,1²-2×1+a = 0,a=1。

圆心角90°是¼圆,所以该扇形面积=¼π2²=π。

解:由3x-2>1得x>1;由x+1<3得x<2;不等式组的解集是1<x<2。

解:由平方差公式得 a²-1=(a-1)(a+1),所以式子=a+(a+1)=2a+1,把a=5代入得2×5+1=11。

分析:OP是公共边,∠AOC=∠BOC,只要公共边对角∠PDO=∠PEO,就符合AAS。
证明:∵ PD⊥OA,PE⊥OB,
∴ ∠PDO=∠PEO=90°,
∵ 在△OPD和△OPE中
∠PDO=∠PEO
∠AOC=∠BOC,
OP=OP,
∴ △OPD≌△OPE。(AAS)

分析:学生人数和书的价钱都是未知数,于是需要寻找两个等量关系,题中明显有两个等量关系。
解:设学生有x人,书的价钱是y元,根据题意列出下面两条方程
8x=y+3,①
7x=y-4。②
①-②得
x=7, ③
把③代入①解得
y=53。
答:学生有7人,书的价钱是53元。

分析:确定函数关系就是确定k值,代入非零一组x,y值可解得;已知函数值反推自变量值,把函数值代入函数解方程即可。
解:(1)把x=2,y=19代入y=kx+15,即
2k+15=19,解得k=2。
即它们的函数关系式是:y=2x+15。
(2)把y=20代入y=2x+15得
2x+15=20,解得
x=2.5。
答:所挂的物体的质量是2.5kg。

解:(1)4万元是4人,8万元是2人,补全的条形统计图如下:

(2)月销售额是4万元的人数最多(众数——集合中最多个数的元素);
3万元1人,4万元4人,5万元3人,1+4=5,5+3=8,所以第8个数都是5,第8个数是中位数,即中间的月销售额是5万(中位数:集合按顺序排序后,奇数个数集的中间元素或偶数个数集中间两个元素的平均值。);
(3+4×4+5×3+7+8×2+10×3+18)/15=7,即平均月销售额是7万元。
(3)月销售额定为平均数,即7万元比较合适。

(1)解:从图上可以看到△ABC是等腰直角三角形。
∵ ∠ADB=∠CDB,
∴ AB=BC, (相等圆周角对应的弦相等)
又 AC是圆O的直径,
∴ ∠ABC=90° (直径所对的圆周角是直角)
∴ △ABC是等腰直角三角形。
(2)分析:由于∠ADC是直径对角,所以是直角,AD已知,只要知道AC的长,CD可求,由(1)的结果可算。
解:∵ △ABC是等腰直角三角形,
∴ AC²=2AB²,得AC²=4, (勾股定理)
又 AD=1,
∴ CD²=AC²-AD²=4-1=3,(勾股定理)
即 CD=√3(根号3)

分析:(1)因为抛物线只有2个常数需要确定,所以只要2点,A点已知,由AB=4可知B点可求;(2)当P点与B或A重叠时,△CPQ的面积都是0,所以P点变化中必有最大值。抛物线已确定,则C点确定,这样△CPQ的面积可以表达为P点的函数,求这个函数的最大值即可。
解:(1)设B的坐标是(x,0),由A的坐标是(1,0),AB=4,得
|x-1|=4。
解得x=-3 或 x=5,
即B点的坐标是(-3,0)或(5,0)。
把(-3,0)和(1,0)代入函数解析式得方程组
9-3b +c=0,①
1+b+c=0,②
①-②得
8-4b=0,
解得 b=2。
把b=2代入②解得
c=-3。
即得一种解析式是
y=x²+2x-3。
把(5,0)和(1,0)代入函数解析式得方程组
25+5b+c=0,③
1+b+c=0,④
①-④得
24+4b=0,
解得b=-6。
把b=-6代入④得
-5+c=0。
解得c=5。
即得另一种解析式是
y=x²-6x+5。
(2)由于两条抛物线是对称的,不失一般性,只考虑第一条抛物线,C点的x坐标是(-3+1)/2=-1,把它代入解析式得y坐标是-4,即C点坐标是(-1,-4)。得
S△ABC=½4×4=8。
∵ PQ//BC,
∴ △APQ∽△ABC。(平行于底的直线所截的三角形与原三角相似。)
S△APQ/S△ABC=(AP/AB)² (相似三角形面积比是相似比的平方。)
即 S△APQ=(AP/AB)²·S△ABC。
又 ∵ △APC与△ABC等高,
∴ S△APC/S△ABC=AP/AB。(等高三角形面积比等于底边比。)
即 S△APC=(AP/AB)·S△ABC。
S△CPQ= S△APC-S△APQ=(AP/AB)·S△ABC-(AP/AB)²·S△ABC。
设(AP/AB)=x,则
S△CPQ=8x-8x²=2-8(x-½)²。
∴ 当x=½时,S△CPQ最大,是2。
由 (AP/AB)=½得
AP=½AB=2,
即P点坐标是(-1,0)。