知识要点：科学记数法是等值把小数点移到第一个非0数之后，指数的绝对值是移动位数，向左为正，向右为负。答案：B

轴对称图形与图形轴对称：轴对称图形来源于图形轴对称，但它们不是相同的概念。图形轴对称是一对图形至少有一条对称轴。研究图形轴对称的过程中，发现某些图形可以至少有一条对称轴把它切为两个图形，这两个图形轴对称，我们就把这种图形叫做轴对称图形。轴对称图形是图形的本身特性，图形轴对称是指两个图形的相似方式。图形旋转与旋转对称图形：一个图形，以图形的边上或外面的一点为转轴转动，就是图形旋转；我们发现某些图形以图形内部的一点为转轴，转动一个角度后能够完全与自己重叠，这样我们把这类图形叫做旋转对称图形。
旋转对称图形与中心对称图形：旋转对称图形有一个产生重叠的最小转角，如果这个角至少有一个整数倍是平角（180°），那么这个旋转对称图形就是中心对称图形。轴对称图形与中心对称图形的判定方法：首先用我们的本能定位图形的中心（人类的大脑有超强的图像计算能力，这个能让计算机崩溃的问题，人类可以轻而易举的完成），然后经过这个中心点和图形中的某些关键点（一般是图形的顶点）能否把图形分为图形轴对称的两个图形，如果能找到这样一条直线，那么这个图形就是轴对称图形；以这个中心点转动图形180°，看看能否重叠来判断是否是中心对称图形。答案：A

知识要点：这题很简单，一看就知道答案，但如果要说明得到答案的依据，还是要想一想。它的依据是等量公理：等量加、减、乘、除以（非0）仍是等量。∵ ∠AOC=∠BOD=90°，∴ ∠AOC+∠BOD=180°，∴ ∠AOC+∠BOD-∠BOC=180°-∠BOC，∴ ∠AOD=180°-∠BOC，∴ ∠BOC=180°-∠AOD=180°-126°=54°。
答案：C

知识要点：这题也很简单，不过别着急选答案，实际的不等式是a>1。一定要用不等式有关公理：（1）不等量加、减等量，乘或除以（非0）正等量，不等号方向不变；不等量乘或除以（非0）负等量，不等号方向改变；
（2）不等式的传递：a>b和b>c，那么a>c；a<b和b<c，那么a<c；
（3）两对正不等量，两个大的量相乘的积比两个小的量相乘的积大。
思路分析：a>1，两边同时乘-1，方向改变，-a<-1，通过这两个条件选择答案就行。
答案：B

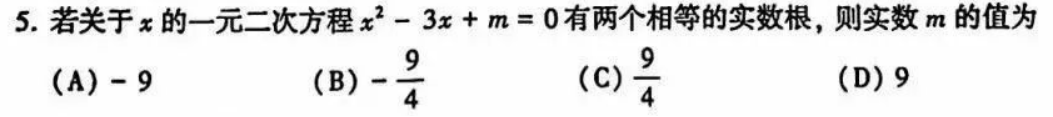知识要点：只有a(x+b)²=0模式的方程才有可能是两个相等的实根。
思路分析：有两个相等的实根，那么方程可以写为(x+t)²=0（t为两个相等的实根），展开后是x²+2tx+t²=0，用系数对比可解。
答案：C

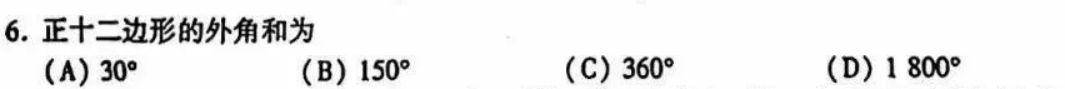知识要点：（凸）多边形的外角和，实际上就是转一圈回到原来的方向，当然是360°；因为一个内角和它的外角和是180°，这样可得内角和n·180°-360°=(n-2)·180°。
答案：C

知识要点：概率是一个极限，也就是一个随机样本的样本数趋向无穷大时，某种情况出现的几率。数学家们发现概率等于随机本体中随机对象的占比。思路分析：整理关键是随机对象的个数，第一次正面向上、第二次反面向上（即正面向下），简称为“上下”，除了这个还有“上上”、“下上”和“下下”三种，“上下”这个对象在本体（“上上”、“上下”、“下上”、“下下”）中占比是1/4，所以概率是1/4。另外，每次的某一面向上的概率都是½，因此总概率是1/4。答案：A

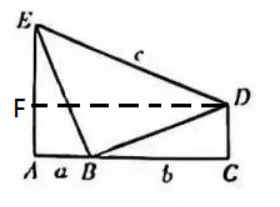
知识要点：三角形两边和大于第三边；直角三角形中斜边大于直角边。
思路分析：c是直角梯形的斜腰，a+b是垂直腰，易得①正确；a和b是直角三角形的两直角边，√(a²+b²)是它的斜边，所以②正确；c/√2是等腰直角三角形的直角边，又是小直角三角形的斜边；所以③正确。
【解答】∵ ∠A=∠C=90°，△EAB≌△BCD，
∴ AE=CB=b，AB=CD=a，BE=DB，AE//CE，∵ AB<BC，∴ 过D作DF//CA，交AE与F，如下图，
∴ DF=CA，∠EFD=90°，
∴ DF<DE，即①a + b < c；（直角三角形中直角边小于斜边）
∵ BE=√(a²+b²) ， （勾股定理）∴ ②a + b > √(a²+b²)，  （三角形两边和大于第三边）∵ ∠AEB+∠ABE=180°-90°=90°，∠AEB=∠CBD，
∴ ∠EBD=180°-(∠ABE+∠CBD)=180°-90°=90°，∴ EB=ED/√2，∴ ③√2(a+b) > c。

答案：D

知识要点：分母或者除数不可以为0，开偶次方的底数不可以小于0。
【解答】x-2≠0，得 x≠2。

知识要点：因式分解尝试优先顺序——提取公因式，x²+(p+q)x+pq模式分解，abx²+(aq+bp)x+pq模式分解，平方差公式，完全平方公式，奇数幂之和或差（例如：x³+1、x³-1）。【解答】原式=y(x²-y²)=y(x-y)(x+y)。

知识要点：对于分式方程，首先要确变量的取值范围（定义域），然后再去分母，得到答案后检查是否在取值范围内。【解答】由5x+1≠0，得 x≠-1/5；由2x≠0，得x≠0；去分母原方程转化为
6x=5x+1，解得x=1（在取值范围）。

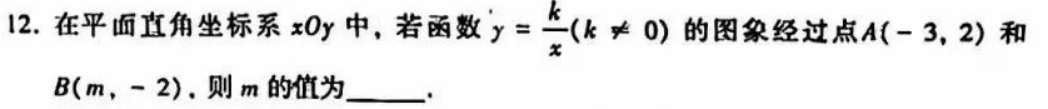思路分析：同一个已知点可以确定函数解析式，把未知点代入解析式得方程，解得m值。
【解答】把A(-3,2)代入函数得，
2=-k/3，得k=-6，所以函数解析式是
y=-6/x。
把B(m,-2)代入得方程
-2=-6/m，
解得 m=3。【快速解答】由于A(-3,2)和B(m,-2)的函数值的绝对值相等，符号相反，所以m一定是-3的相反数3。

知识要点：基本假设——样本比例与实际的比例一样。
【解答】1000×(17+6)/50=460（个）

知识要点：平行线所截的另一对平行线所得线段相等；三角形中平行于底边的直线把另外两条边截成正比例的两对线段。
思路分析：通过平移BC，使A、B两点重合，那么，BE/EC=AF/FD。
【解答】过A点作AC'//BC，交EF于E'，如下图，
∵ AB//EF//CD，
∴ BE/EC=AE'/E'C'=AF/FD=3/2。

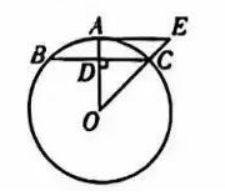知识要点：垂直于弦的直径平分弦；经过切点与圆心的直线垂直于该切线，反过来，经过圆上一点与直径垂直的的直线与圆相切。初中需要掌握的有关圆的知识还有：等弧或弦对应（优劣相同）圆周角相等和圆心角相等；直径所对的圆周角是直角；圆切角与对应的圆周角相等；等弦到圆心的距离相等。
思路分析：不能得到△OAE是等腰直角三角形，所以AE=OA，问题转化为圆的半径，OC也是半径，即Rt△ODC中的斜边，由圆的性质可得。
【解答】∵ AE是○O的切线，OA和OC是○O的半径，
∴ ∠OAE=90°，∵ ∠AOC=45°，∴ ∠AEO=90°-45°=45°=∠AOC，
∴ AE=OA=OC，
∵ OA⊥BC，BC是○O的弦，
∴ DC=BD=½BC=1，∠ODC=90°，∴ AE=DC/sin∠AOC=1/sin45°=√2。

思路分析：如果是一名学生，那么他只能从头到尾完成，所需时间就是加和；如果两名学生，那么非关联工序可以平行操作，如何作出关联图呢？一般倒序的方法作出关联图，如下图，工作安排就明显了：一位同学干A，另一位干B，同时完成；然后一位干D，另一位干C和G，也是同时完成，最后E、F每人干1道。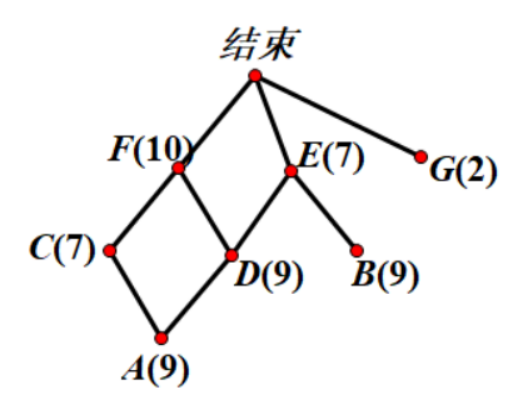
【解答】一个同学干，9+9+7+9+7+10+2=53（分钟）；两个同学干至少用时=9+9+10=28（分钟）。

代数式运算要点：开平方或开立方时，先把底数分解为2个因数的积，第一个是平方数或立方数，第二个是商，第一个因数开方后写在根号左边，第二个留在根号内，如果底数是一个平方数或立方数就没有根号部分。需要记住的锐角三角函数（sin,cos,tan）的角度是30°、45°和60°。不用死记硬背，30°和60°是一块三角板（三边分别是1，√3，2），45°又是另外一个三角板（三边分别是1，1，√2）。非0数的0次方都是1。负整数次方相当于相反数次方的倒数。 【解答】原式=4·√3/2 + 3 + 2 -2√3=5。

知识要点：不等式组是所有不等式的交集。【解答】分别解两条不等式，得
x>1和x<2，所以不等式组的解为1< x < 2。

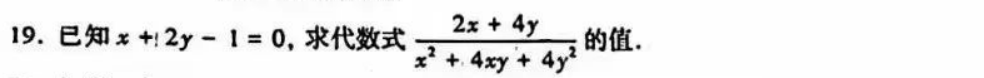思路分析：从已知代数式求未知代数式的值，往往不是通过已知条件求出每个代数的值，然后代进去计算，而是使用类似于换元的方法的等值变换——整式运算、因式分解等，从而使代数式只含已知值的代数式。本题显然要使用因式分解。【解答】∵ x+2y-1=0，
∴ x+2y = 1，
原式=2(x+2y)/(x+2y)²=2/(x+2y)=2/1=2。

思路分析：（1）首先容易得到四边形AECF是平行四边形，那么只要证明有一个角是直角就行。由条件可知两个同旁内角相等而得证。（2）由于BC=EC+BE，因此要求EC和BE，由于tan∠ACB已知，所以只要求得AE和BE就行，显然它们是Rt△ABE的2个直角边，由条件不难求出它们。【解答】（1）∵ 平行四边形ABCD，BE=DF，
∴ AF//EC， AF=EC，∴ 四边形AECF也是平行四边形。∵ 在△AEF和△EAC中，
AF=EC，AE=EA，EF=AC，
∴ △AEF≌△EAC。（SSS）
∴ ∠EAF=∠AEC，∵ ∠EAF+∠AEC=180°，  （平行线同旁内角互补）
∴ ∠EAF=∠AEC=90°。
∴ 四边形AECF是矩形。
（2）∵ ∠AEB=90°，AE=BE，
∴ BE=AE=AB/√2=2/√2=√2，∵ ∠AEC=90°，tan∠ACB=½，
∴ EC=AE/tan∠ACB=2√2，∴ BC=BE + EC = 3√2。

思路分析：这题用算术的方法也许可以求出来，不过对于初中生来说，不应该这样做。把一些必要的未知量设为未知数，已知数和未知数同等对待，找出题目提供的等量关系，列方程或方程组解答。
【解答】设边宽和天头长分别为x, y，那么
地头长=⅔y，x=(y+⅔y)/10=1/6y,
100+5/3y=4(27+2x)，
解得y=24，则x=4。
答：边宽4cm，天头24cm。

思路分析：（1）两点确定一直线，如下图，所以A、B两点的值可以确定函数的解析式；过(0,4)平行于x轴的直线是y=4，代入直线解析式可求x值；

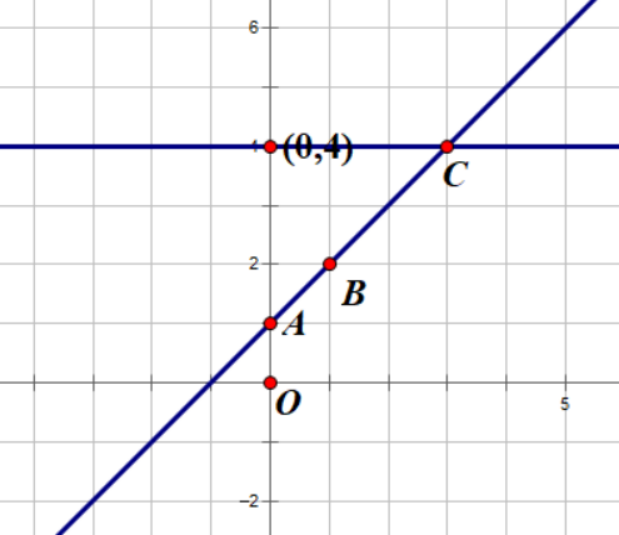
（2）不等式在坐标系中是一个区域，x<3就是x=3的直线左边区域（开区间，不含直线本身），y<4是y=4的直线的下面区域（不含直线本身），相交的区域就是本题的定义区间，如下图，不难发现，只有n=2时才符合要求。

【解答】（1）列方程组
b=1,
2=k+b,∴ 函数解析式是y=x+1,∵ 过(0,4)平行于x轴的直线是y=4，解方程4=x+1,得 x=3，即
C点坐标(3,4)。

（2）由函数⅔x+n=x+1的解是x=3，得n=2。由题可知当n>2时，就有y=⅔x+n的函数值在x<3时大于4，不符合要求；当n<2时，就不能保证⅔x+n>x+1，所以也不符合要求；所以只有n=2时才能满足要求。

数据统计中的指标：平均数，总数除以个数，反映样本数据的平均水平。中位数，样本排序后中间的一个值（奇数个数）或两个值的平均值（偶数个数），反映样本的中间水平；中位数与平均数的差距反映样本的概率分布的对称状况，差距越小越对称。众数，样本中出现次数最多的数（注意：是数本身不是次数），众数反映数据的集中趋势；如果样本每个数出现的次数都一样，那么就没有众数；如果样本有多个数出现的次数都最多，那么它们都是众数。方差，度量随机变量和其数学期望值之间的偏离程度。方差指数级别放大差距，例如，差值是10和1，那么差距只是9，但方差的差距99，因此如果有个别偏离大的值，方差会变得很大。数据统计中的方差是一种特殊的方差，是指每个样本值与全体样本值的平均数之差的平方值的平均数（即把样本平均数作为期望值的方差）。为了更深入理解期望值，下面举例说明。如下图，如果把y=x+5当作期望值，那么方差=(1+9+16+1)/4=6.75；如果把y=4当作期望值，那么方差=(64+0+0+100)/4=41。

思路分析：（1）如果用Python编程计算，那是一件容易的事，不过这里可不允许。但由于给出的数据已经排序，中位数不难；众数从头到尾扫一遍获取最多个数的数（全部）。（2）先求平均数作为期望值，然后计算方差。（3）有两个168，一个172，要提高平均数的办法就是增加身高大于(168*2+172)/3≈169，除了已经选的一个（172）外，还有三个分别是170、172、175，也就是所要从三个数中选2个，使五人的方差<32/9，平均值最大。
【解答】（1）中位数m=(166+166)/2=166；众数扫描算法如下：
数162:2次，数165:3次（后面的次数没有大于等于3的），所以众数n=165。（2）平均数：P甲=(162+165+165+166+166)/5=164.8；
P乙=(161+162+164+165+175)/5=164.14；
甲方差=(2.8²+0.2²+0.2²+1.2²+1.2²)/5,
乙方差=(3.14²+2.14²+0.14²+0.86²+10.86²)/5，
显然乙方差大，所以选择甲组。（3）原平均值=(168*2+172)/3=170-⅔，要提高平均值，则要从170、172、175三个数中选两个，枚举计算平均数与方差：
①选170,172，那么5个数分别是
168,168,170,172,172，平均数=170>170-⅔，
方差=(2²+2²+0+2²+2²)/5=16/5<32/9；②选170,175，那么5个数分别是168,168,170,172,175，
平均数=170+3/5>170-⅔，
方差=(2.6²+2.6²+0.6²+1.4²+4.4²)/5>5>32/9；（不符合要求）；
③选172、175，那么5个数分别是
168,168,172,172,175，
平均数=171，
方差=(3²+3²+1+1+4²)/5=36/5>32/9；（不符合要求）；所以，只有①符合，即选170,172。

知识要点：初中需要掌握的有关圆的知识——等弧或弦对应（优劣相同）圆周角相等和圆心角相等；直径所对的圆周角是直角；圆切角与对应的圆周角相等；等弦到圆心的距离相等；经过切点与圆心的直线垂直于该切线，反过来，经过圆上一点与直径垂直的的直线与圆相切。

思路分析：（1）DB平分∠ADC，即∠ADB=∠CDB，由条件是容易达到的，由∠BAD和∠ACD所对的弧加起来是一个圆周，即得两角和是180°，而且两角相等（因为三角形中其他两对角都相等），得解。（2）用BF去反推半径这种算术思维方式是很难完成这题的，初中生应该用代数的思维思考问题，也就是说，设半径为r，建立r与BF的等式关系（方程），解方程得到所求。由条件可是三角形ACD是正三角形，这样不能用半径表达AF和AB，由AF-AB=BF列方程，可解出半径。【解答】（1）∵ BD平分∠ABC，∴ ∠ABD=∠CBD，∵ ∠BAC=∠ADB，∠BAC=∠BDC（同弧圆周角），∴ ∠ADB=∠CDB，∴ DB平分∠ADC。∵ ∠BAD=180°-(∠ABD+∠ADB)，∵ ∠BCD=180°-(∠CBD+∠CDB)，∴ ∠BAD=∠BCD，∵ ∠BAD+∠BCD=180°，∴ ∠BAD=∠BCD=90°。（2）∵ 在△ABD和△CBD中，∠ABD=∠CBD，∠ADB=∠CDB，BD=BD，∴ △ABD≌△CBD，∴ AD=CD，∵ AC=AD，∴ △ACD是等边三角形，∴ ∠ADC=60°，∠ADB=∠FAC=30°。设圆的半径为r，那么AC=AD=2rcos30°=√3r，AB=2rsin30°=r，AF=ACcos30°=(3/2)r，∵ AF-AB=BF，BF=2，∴ (3/2)r-r=2，∴ r=4。

【解答】（I）下图：
（II）函数图像如下图，

（1）但第一次4.5时，用水量最少，是7.7，节约19-7.7=11.3单位；
（2）有图可知，但用第一次水量是6时，要达到要求，总用水量约是8.3，如果总用水量没达到这个数，清洁度会下降，所以C<0.990。

抛物线的一些特性：二次系数，决定开口大小和方向：大于0，开口向上，有最小值；小于0，开口向下，有最大值。如下图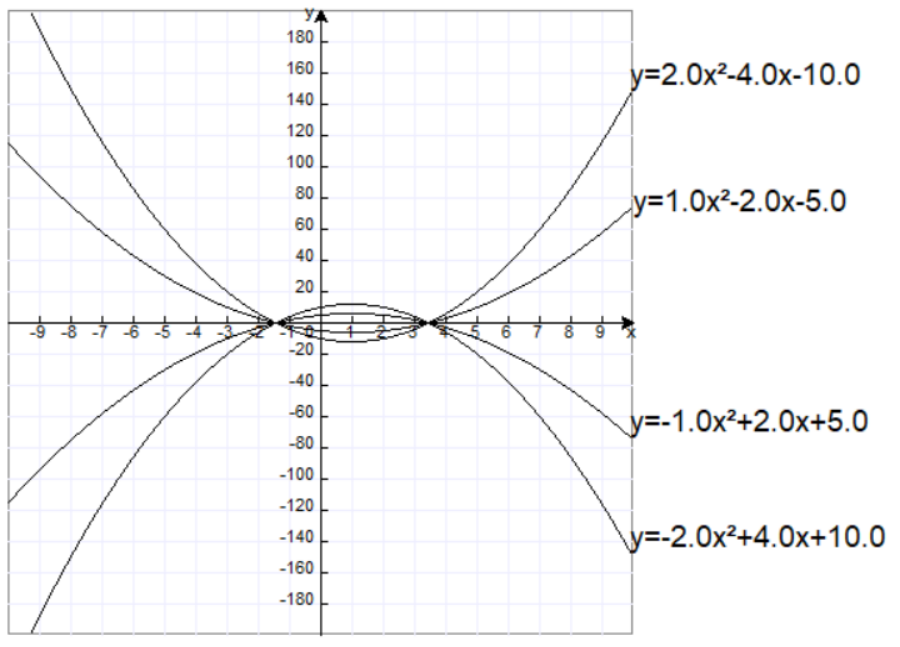：过最大或最小值点的平行于y轴的直线是抛物线图像的对称轴。如下图：平行于x轴的直线如果与抛物线交于不同的2点，那么这两点关于对称轴对称（假设对称轴是x=a，两个交点的x坐标是x1,x2，那么x1+x2=2a）。如下图：当与x轴相交于两个点，那么这两个点的x坐标是一元二次方程的两个实根。两个实根之和与积与函数的系数有对应关系：a(x-x1)(x-x2)=ax²+bx+c，ax²-a(x1+x2)x+ax1x2=ax²+bx+c，
所以 x1+x2=-b/a，x1x2=c/a。
抛物线的两种解析式与它们之间的换算：普通式y=ax²+bx+c，顶点式y=a(x+p)²+q（顶点是(-p,q)），p，q与b，c的换算关系：a(x+p)²+q=ax²+bx+c，ax²+2apx+ap²+q=ax²+bx+c，所以 p=b/2a，q=c - b²/4a。x=0时，得到在y轴上的截距ap²+q。在研究函数图像时，往往使用顶点式。思路分析：（1）对称点的横坐标的平均值是对称轴；（2）由于a>0，所以抛物线开口向上，如果对称轴是x>½，由于对称，就无法保证。
【解答】（1）t=(1+2)/2=3/2；（2）t≤(0+1)/2=1/2。
思路分析：（1）由于∠MDE是△EDC的一个外角，易得△EDC等腰三角形，得证；（2）连接（1）中的ME，如下图，

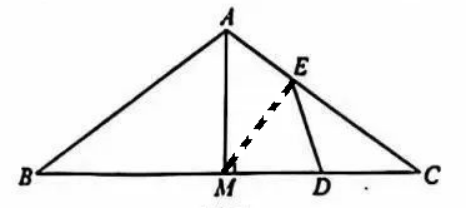
由直角三角形的中位线定理的逆定理可知ME⊥AC，那么可以断定∠AEF=90°。由（1）的证明过程，很自然想到延长DE交AC于G，连接FG，如下图，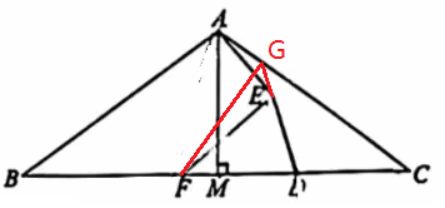

与（1）同样的步骤可以FG⊥AC，因此考虑E点的运动轨迹始终是以AF为直径的圆周上（虽然AF是变化的），为了证明这一点，连接AF，取AF的中点N，连接NE，如下图，

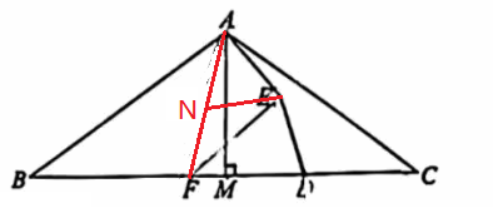
现在只要证明NE=NF，就行了。由于△AMF是直角三角形，连接NM，如下图，

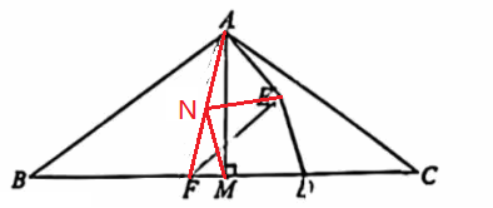
那么NM=NF，问题转化为证明NM=NE，自然地连接ND，如下图，

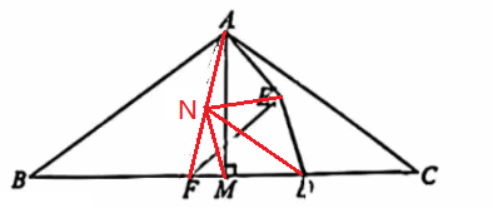
由条件知道DM =DE，加上要证明的NM=NE，那么断定△DMN≌△DEN，这样问题转化为证明△DMN≌△DEN。用于D是FC的中点，和∠MDE=2∠C，不难得到∠MDN=∠EDN=α，加上DM=DE，得证。【解答】（1）∵ ∠MDE=∠DEC+∠C=2α，∠C=α，∴ ∠DEC=∠C=α，∴ DE=DC，∵ DM=DE，∴ DM=DC，即D是MC的中点。（2）由（1）的延伸可以断定∠AEF=90°。如上图，连接AF，取中点N，连接NE，ND，NM，∵ DF=DC，∴ DN//CA，（△AFC中位线）∴ ∠MDN=∠C=α，∵ ∠MDE=2α，∴ ∠MDN=∠EDN=α，∵ 在△MDN和△EDN中，DM=DE，
∠MDN=∠EDN，DN=DN，∴ △MDN≌△EDN，∴ NM=NE，∵ N是Rt△AMF的斜边上中点，∴ NM=NF=NA=NE，∴ ∠AEF=90°。（直角三角形斜边中线定理的逆定理）

思路分析：这题说得玄乎，所谓的“关联点”，就是圆的直径延长线上取一点，作圆的切线，连接延长线的始端点和切点所得的弦，所取的点是这弦的“关联点”。①C3一定不是，因为与A和B1的的连线都不过圆心，连接C2C3，可知它切○O于B1点，因此C1和C2都是。②AB2的关联点除了C1外，还有C2的对称点，不难得到OC的长。【解答】①C1和C2，②√2。思路分析：不失一般性，规定SP是过圆心的，因此P有两点，Q是切点，也有2点，不过是对称的，所以只要考虑一点，如下图，

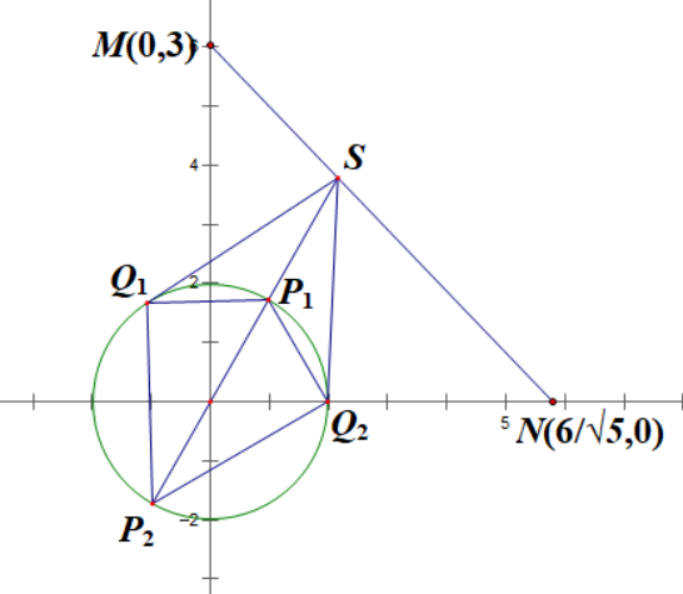
由于∠P1SQ1与S到圆心的距离有关，距离越远，角度越小，P1Q1越大，因此M点时得到最大值，同理P1S⊥MN时最小，由勾股定理通过P1Q1的范围得到P2Q1的范围。解题过程中不要忘记使用一个重要的定理：圆切角等于该弦所对的圆周角（自己证明也不是难事）。对应本题，∠SQ1P1=∠Q1P2P1，这样，连接圆心OQ1，过P1作OQ1的平行线交SQ1于K，如下图，这样可以得到在S运动过程中保持相似的两个Rt△Q1P1K和Rt△P2P1Q1，问题可解。【解答】如下图，S在M点时，P1Q1的最大值，这时P2Q1是最小值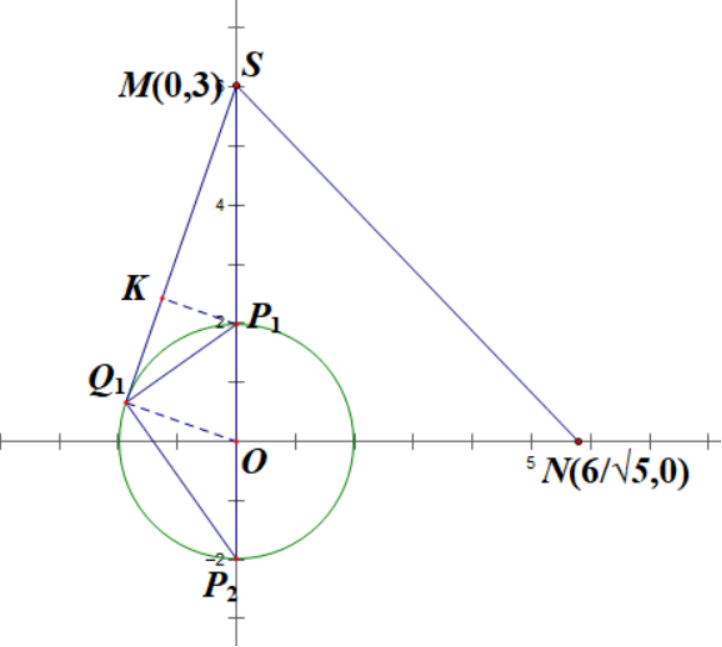，连接OQ1，作P1K//OQ1,交MQ1于K点，∵ MQ1是○O的切线，∴ P1K/Q1O=MP1/MO=⅔，∴ P1K=⅔，∵ 在Rt△Q1P1K和Rt△P2P1Q1中，∠KQ1P1=∠Q1P2P1（圆切角等于圆周角），∴ Rt△Q1P1K∽Rt△P2P1Q1，∴ P2P1/Q1P1=Q1P1/P1K，∴ (Q1P1)²=P2P1·P1K=4/3，∴ Q1P1=⅔√3。（t1最大）∵ (Q1P2)²=2²-(Q1P1)²，∴ Q1P2=⅔√6。（t2最小）如下图，当SP1⊥MN时，

∵ MN的斜率=(0-3)/(6/√5)=-√5/2，∴ OS的斜率=2/√5，∴ MN解析式是y=-(√5/2)x+3，OS解析式是y=2/√5x，∴ S的坐标，解方程 -(√5/2)x+3 = 2/√5x 得x=⅔√5，y=4/3，∴ OS²=(⅔√5)²+(4/3)²=4，∴ OS=2，∴ P1S=1，同理可得，Q1P1=1。（t1最小）Q1P2=√3。（t2最大）∴ 如果t是Q1P1，那么它的范围是1≤t≤⅔√3;如果t是Q1P2，那么它的范围是⅔√6≤t≤√3。