要点：指数的绝对值与小数点移动位数相等，左移是正，右移是负。
答案：B

要点：绝对值、偶次方和偶次开方一定是非负数，非零数0次方是1。
答案：D

因式分解的尝试步骤：提取公因式，x²+(p+q)x+pq模式、abx²+(aq+bp)x+pq模式、平方差公式，完全平方公式，奇数幂之和或差（例如：x³+1、x³-1）。答案：A

要点：矩形对角线相等，把矩形分成2对等腰三角形。
答案：D

要点：左右平移，y坐标不变，上下平移x坐标不变。
答案：C

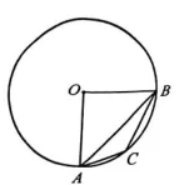要点：所对的弧同样长，圆周角是圆心角的一半。
答案：D

要点：乘绝对值大于0小于1的数，结果的绝对值会缩小。
答案：B

要点：换元法套用平方差公式，原式=a[(x-m-k/2)+k/2][(x-m-k/2)-k/2]=a[(x-m-k/2)²-(k/2)²]
答案：A

要点：平均数、中位数、众数和方差的概念，平均数是3，方差是2，那么数值是2,3,4三个数。
答案：C

要点：大正方形的面积等于小正方形面积加四个三角形面积，而它们的面积之比是1：n，所以2AF·FB+1=n，把tanα=tan²β变为线的代数式，由于EF²=1，所以是FB/AF=FB²，即FB=1/AF，所以n=3。
答案：C

要点：把底数分解为一个最大平方数和一个非平方数的积，平方数开方后写在根号左边。
答案：-√2

要点：同位角相等，外角与两个对内角关系。
答案：90

要点：概率是一个极限，是无限多次取样趋向的比例，“摸出一个球是红球的概率为2/5”实际的意思是摸出一个球，统计它的颜色并计数，然后把球放回去，如此无限多次后，发现出现是红球的次数是总次数的2/5。数学家们发现——概率与该类对象的占比相等。那么，本题就是6个红球占比2/5，求白球数量。答案：9

要点：圆内接正六边形的边长等于半径，连接OA，OC，OE后得到三个棱形，所以答案是2。
答案：2

要点：这个实际是问三点相互连线中，与x=1的交点，y坐标最大的值。显然，AC<AB<BC，因此计算B、C两点的值就行了。由图直接得到答案是5。
答案：5

要点：小三角形是大三角形的中位线围成，由轴对称，BF连线垂直于DE和AC，设AB=AC=1，则BC=k，设CF=y，则FA=1-y，容易得到方程：
1²-(1-y)²=k²-y²，解得y=k²/2，代入即得答案。
答案：k²/(2-k²)

分析：有两个不相等的实根的依据是b²-4ac＞0，显然只有②和③合适。
【解答】

分析：根据2个图的对比，A60人占60%可计算抽样人数；知道抽样人数后，根据条形图可计算B的人数，因此可以补全条形图；由B的占比可计算，从而B的人数也可计算。
【解答】

分析：（1）方法比较多，不过对角线相互平分是最简便的；（2）由等高的三角形面积比等于底之比可以计算。
【解答】

分析：（1）函数图像的交点要符合2个函数的数量关系，因此可以推算系数的值。（2）经过原点的直线y=ax+b，b=0，因此只要计算出CD直线的解析式，问题就解决。
【解答】

分析：（1）由相似三角形不难求出；（2）AB·BC=1，问题转化为AE·CF=AB·BC，即AE/BC=AB/CF，由相似三角形可证；（3）AE=AD-ED，BE=BG+GF，直角三角形ABE的勾股定理方程可计算出结果。
【解答】

分析：（1）①由于已知(2,1)点，还知道(-1,4)点，列方程组可求a,b。②开口向上的抛物线是左侧，开口向下的是右侧。（2）由点(2,1)和(0,1)可以用a来表示b，因此m,n,p都可以表示为a的代数式。另外(2,1)和(0,1)y坐标相等，即它们是对称点，所以对称轴是x=1，因此m,p的代数式是相同的，有条件可算出a的取值范围。
【解答】

分析：（1）如果△CBG是等腰三角形，那么问题解决，通过对顶角相等，同弧圆周角相等，两对角90°四边形另一对角互补可以得到。（2）变为BC/BO=BG/BC，可见连接OC，证明两个三角形相似就行。（3）能通过初中几何来证明的度数无非是30°、45°和60°，是45°的几率比较大，因此猜45°。因为CF⊥AD，如果AF=CF，则△AFC是等腰直角三角形。因此问题实际是“证明△AFC是等腰直角三角形”。等腰三角形的三线合一，反过来，三线合一的三角形是等腰三角形。∠BCA是直径所对的圆周角，所以BC⊥AC，而且O是圆心，过圆心的垂线是弦的垂直平分线，那么只要证明OF与BC平行，问题解决，这个由（1）可知△CEG是等腰三角形，因此问题不难了。【解答】