有关整数那点事：整数包括正整数、0和负整数，正整数和0构成自然数。

答案：A

轴对称图形与图形轴对称：轴对称图形来源于图形轴对称，但它们不是相同的概念。图形轴对称是一对图形至少有一条对称轴。研究图形轴对称的过程中，发现某些图形可以至少有一条对称轴把它切为两个图形，这两个图形轴对称，我们就把这种图形叫做轴对称图形。轴对称图形是图形的本身特性，图形轴对称是指两个图形的相似方式。图形旋转与旋转对称图形：一个图形，以图形的边上或外面的一点为转轴转动，就是图形旋转；我们发现某些图形以图形内部的一点为转轴，转动一个角度后能够完全与自己重叠，这样我们把这类图形叫做旋转对称图形。
旋转对称图形与中心对称图形：旋转对称图形有一个产生重叠的最小转角，如果这个角至少有一个整数倍是平角（180°），那么这个旋转对称图形就是中心对称图形。轴对称图形与中心对称图形的判定方法：首先用我们的本能定位图形的中心（人类的大脑有超强的图像计算能力，这个能让计算机崩溃的问题，人类可以轻而易举的完成），然后经过这个中心点和图形中的某些关键点（一般是图形的顶点）能否把图形分为图形轴对称的两个图形，如果能找到这样一条直线，那么这个图形就是轴对称图形；以这个中心点转动图形180°，看看能否重叠来判断是否是中心对称图形。答案：B。
题型要点：除数或分母不可以等于0，开偶次方的底数不可以小于0。因此α-4≥0，所以α≥4。
答案：D。
指数运算与幂运算的对应：同底幂相乘<==>指数相加
同底幂相除<==>指数相减异底同指数幂相乘<==>指数不变，底相乘异底同指数幂相除<==>指数不变，底相除幂之幂<==>指数相乘幂开方<==>指数相除答案：A。
要点：过O点作垂线就是光反射的法线，法线与入射光的夹角是入射角，反射光与法线的夹角是反射角，入射角与反射角相等。容易得到答案。
答案：C。
要点：平面上不在同一直线上的不同三个点唯一确定一个圆，因此，所有的圆都要有P点，ABCD四点取2的组合是3+2+1=6。
答案：D。
要点：单项式的系数是数值，不是代数字母。
答案：-5。
要点：指数的绝对值与小数点移动位数相等，左移是正，右移是负。答案：1.8×10^7。
整式运算要点：平方差公式优先。原式=(a+1-a)(a+1+a)=2a+1。
答案：2a+1。
分析：由平行线的同位角可知∠ACB=∠α=60°，所以△ABC是等边三角形。
答案：2。
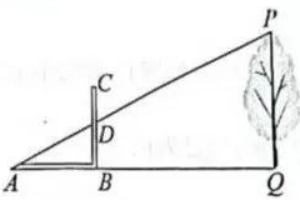分析：利用的是相似三角形对应边成比例。
答案：6。
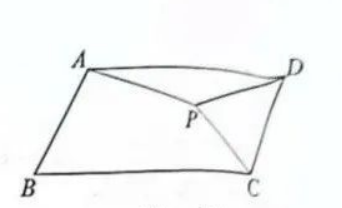分析：连接AC，因为BC=2AB，且∠B=60°，得到AC⊥CD，因此转角可以是90°或270°，另外，过D作平行于AC的线会与○A相切，所以180°也行，如下图。答案：90°或180°或270°。
分析：（1）代数式运算要点：开平方或开立方时，先把底数分解为2个因数的积，第一个是平方数或立方数，第二个是商，第一个因数开方后写在根号左边，第二个留在根号外，如果底数是一个平方数或立方数就没有根号部分。需要记住的锐角三角函数（sin,cos,tan）的角度是30°、45°和60°。不用死记硬背，30°和60°是一块三角板（三边分别是1，√3，2），45°又是另外一个三角板（三边分别是1，1，√2）。非0数的0次方都是1。（2）共用1边，另一对边相等，平分的2角相等，符合边角边条件。
【解答】

分析：（1）已知一边作三角形，以这边为直径作圆，圆上的点是直角三角形，圆内的点是钝角三角形，圆外的点是锐角三角形。（2）点到线的距离垂线段最短。
【解答】

分析：分式的运算要点，利用分式的基本性质通分合并项，利用“因式分解”约分，运算率的运用。从这个角度看，两位同学的做法都不太好，参考做法如下：
【解答】

分析：这是一种随机事件，由于两名同学没有名次之分，所以一种组合认为是一种可能性，只要求出所有的可能性就可以算出概率。
列表法：一般只适用于在总体中抽取2个元素。如果2个元素有名次之分，就采用全表（对角线除外）。例如，本题改为：先随机选一个同学当主宣传员，后随机选一个同学当副宣传员，列表解法如下。
如果2个元素没有名次之分，就采用半表（对角线上或下部）。例如本题。树状图法：数学中的“树”是一种数据元素的组织形式——数据结构。两棵或以上的树就组成“森林”。树这种数据结构天生就是有先后之分的，因此如果把本题改为：先随机选一个同学当主宣传员，后随机选一个同学当副宣传员，树状图法如下。但本题的两个同学是没有先后之分的，又如何用树状图解决呢？办法是第一棵树标出某个元素（一般是第一个元素）的所有选项，第二棵树是不含已经标出所有选项的元素，如此类推。本题的树状图法如下。

【解答】

分析：（1）两个函数都只有一个待定系数，都经过A(2,3)点，所以都可以确定它们的表达式。（2）由于表达式已确定，B和C坐标可求，这样△ABC的面积也可求。
【解答】

分析：（1）这是小学常见的数学题，每人4棵，也就是原来剩余的20棵每人多发1棵不够分，有25个同学没分到，所以学生人数是20+25=45人。逻辑精妙啊！不过别陶醉于其中，因为这些方法只能用于这一类的问题。初中生应该采用代数的方法解决。代数法解应用题的方法：第一步破题——确定题目中的所有相关量；第二步设未知数——把未知量设为未知数；第三步找等量关系——题目中的“是”、“等于”、“几分之几”、“多少倍”等等是等量关系；第四步列方程解答——等量关系往往比较多，全部用未知数来列出也没必要，一些未知数之间的关系比较简单的可以直接消元。例如本题的（1），可以不算出树苗的总数。
（2）树苗的总数是确定的，但两种树苗的数量可以变化，由于甲树苗价格低，所以总价钱会随甲树苗的增大而减少，费用有上限，所以它的数量有下限。
【解答】

思路：（1）DC⊥BC，即要证明∠DCB=90°，由于AB=AC=AD，用等腰三角形的性质或圆的性质是很容易证明的。（2）用相似三角形的原理也容易计算出来。【解答】

分析：（1）弧长等于圆心角的弧度×半径，为此连接OE，由于半径已知，所以要求∠EOB的度数，由于∠EOB=180°-∠EOA，这样就要求∠EOA，由∠EOA和圆周角∠EDA对着同弧AE，所以∠EOA=2∠EDA，∠EDA=40°，问题解决。（2）如果CB为圆O的切线，那么∠ABC=90°，也就是要证明∠ABC=90°，由于∠C已知，所以只要知道∠BAC就行，又由于∠EAD已知，所以只要知道∠EAB就行，∠EAB和∠EOB同弧，问题解决。
【解答】

分析：（3）什么统计量能够反映总体呢？初中生知道的是三个统计量：平均数、中位数和众数，平均数计算量比较大，这里用中位数或众数。
【解答】

分析：（1）平行四边形的对角线相互平分，如果又相互垂直，那相互是垂直平分线，自然邻边相等，菱形。（2）①根据（1），只要证明对角线相互垂直就行，即证明其中一个三角形的顶角O是90°。由于三角形AOD三边已知，自然使用勾股定理的逆定理证明。②有条件可以知道CO=CE并确定，只要构造出相似的三角形问题就解决。首先就想到过O作BC的平行线，其次想到延长FO交AB一点H，因为O是中心点，HF=2FO。
【解答】

分析：（1）①t=1，即PC=1，由于CD固定并已知，面积S=PD²可求。②PC=t，解析式容易得到。（2）AB是直角三角形的斜边，如果知道两条直角边就解决了，由图2抛物线的端点可得BD²=6，DA²=18，加入DC已知，因此AB可求；另一个方法：如果知道从B到A的运动时间，也可以求出AB的长度，由图可知抛物线的顶点是(4, 2)，因此抛物线可以设为S=a(t-4)²+2，由于BC可求，所以开始B点的坐标是确定的，这样可以推算出a值，从而可以计算到A点的时间。（3）①建立分段函数，补全运动曲线如下图，可知t1,t2关于x=2对称，因此t1+t2可求。②由于第二个分段函数可以由第一个分段函数平移所得，从而得到t3-t1的值（当然可以由两个面积函数相减得到，这里略），因此t1确定，问题解决。
【解答】