一、相交

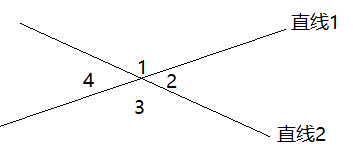
如上图，两条直线过共同点但不重合，这两条直线相交。相交线的性质如下：

（1）一直线同一侧的2个角拼成一个平角。

  例如：∠1+∠2=180°

（2）一直线同一侧的2个角如果相等，则两直线垂直。

  注1：∠1+∠2=180° 和 ∠1=∠2，所以∠1=∠2=90°

  注2：这个也作为垂直的判断标准。

（3）只共用顶点，没有共同边的2个角是对顶角，对顶角相等。

  例如：∠1=∠3

二、平行

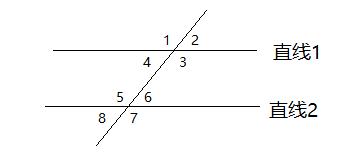
两直线没有共同点（无交点），这两直线是平行直线。作1直线与它们相交，平行直线的性质和判断方法（符合任一性质）：

（1）同侧两内角和是平角（180°）。

  例如：∠3+∠6=180°

  说明：这是欧几里得平行定义，可以简单理解：如果不等于180°，那必然会有一个三角形，与两直线不相交有违。

（2）同侧位置相同的两个角（同位角）相等。

  例如：∠2=∠6

  说明：性质（1）推论，∠3+∠6=180°  ∠3+∠2=180° 所以∠2=∠6。

（3）这两直线之间的不同位置的两个角（内错角）相等。

  例如：∠4=∠6

  说明：性质（2）推论，∠2=∠6  ∠2=∠4 所以∠4=∠6

三、练习题

    下图中直线1和直线2是平行线，（1）列出全部相等的一对角；（2）列出全部和是平角的一对角：

附录：助记词

二直线，过同点，不重合，是相交。
一直线，同一侧，拼二角，成平角。
若相等，二直线，相垂直，角直角。
顶对顶，边不同，对顶角，恒相等。

二直线，恒不交，称作啥，平行线。
作直线，交它们，判方法，下其一:
同一侧，内二角，拼一起，成平角。
同位置，二个角，移一起，能重叠。
不同侧，内错角，移一起，能重叠。

​