一、什么是体

        我们看到的都是物体，每种物体都有各自的属性，比如软硬、冷热、透不透、大小、形状等等，数学里撇开物体的其他属性，只是考虑物体的大小和形状，这就是数学里的体。

二、轴对称与手性

    （1）一个几何体与它在一面平面镜中的镜像轴对称，这平面镜就是对称轴。

    （2）我们会发现长方体、球体、圆锥、圆台等几何体通过平移或旋转就能和它们的的镜像重叠。如果这面镜子把体切开两半，两半也会互相轴对称。

    （3）但我们照镜子时发现：左手掌与左手掌的镜像是无法通过平移和旋转重叠在一起；右手掌与右手掌的镜像也是无法通过平移和旋转重叠在一起；但右手掌与左手掌的镜像可以通过平移和旋转重叠在一起，反之亦然。

    （4）一种几何体不能通过平移和旋转与它的镜像重叠在一起，认为这种几何体具有“手性”。

三、手性几何体的特点

    （1）首先要研究我们左右手的特点：手掌正对自己，拇指向上，发现食指到小拇指的排列顺序左手顺时针，右手逆时针。

    （2）因此得到，手性只不过是几何体一些不一样的部分在空间上的排列顺序造成。

四、几何体的拓扑属性

    （1）把一条丝带扭转180度后接起来就是“莫比乌斯带”。这种带只有一个面，在上面移动的点可以到面上的任何点。

（网络配图）

    （2）几何体也有这样的属性，对于常见的几何体，表面充分圆滑化后会发现只有2种基本几何体，一种是球体，另一种是圆环。因此和可以把几何体进行拓扑分类：拓扑球体、拓扑圆环体、拓扑多圆环组合体（如果眼镜框）。

（网络配图）

五、多面体

    （1）一种几何体的表面全是多边形，这种几何体就是多面体。这些多边形就是多面体的表面，多边形的交线就是多面体的棱。

    （2）由六个长方体围成，相交的棱全垂直，这样的立方体就是长方体。

（网络配图）

    （3）六个面都是相同的正方形的长方体，就是正方体。

（网络配图）

    （4）有两个互相平行并相同的多边形，其面都是平行四边形，这样的柱状多面体是棱柱体或棱柱。如果侧棱都垂直于底，叫直棱柱。

（网络配图）

    （5）最多只有一个非三角形其它面都是三角形的多面体，这样的锥状多面体是棱锥体或棱锥。

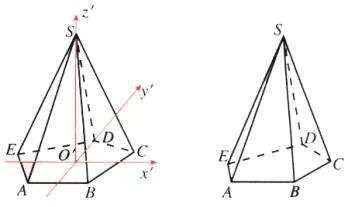
（网络配图）

    （6）用平行于底的平面切去棱锥体的一个小棱锥体，剩下的部分就是棱锥台体或棱锥台。

六、旋转体

    （1）一个平面图形，绕平面上的一直线为轴旋转一周，形成的闭合几何体就是旋转体。

    （2）直角三角形绕一条直角边旋转一周，那是圆锥体。

（网络配图）

    （3）长方形绕一条边旋转一周，那是圆柱体。

（网络配图）

    （4）直角梯形绕直角腰旋转一周，那是圆台体。

（网络配图）

    （5）如果所绕的轴与图形没有共点，旋转一周，那是环体。如果这个图形是圆，这样的旋转体就是圆环。

（网络配图）

    （6）半圆绕直径转用一周是球体。

    （7）旋转体都是轴对称体，对称轴有无数个。

七、柱体、锥体和台体

    （1）上下底相同且平行，任一与底平行的平面被这个几何体所截的图形都与底相同，这样的几何体就是柱体。柱体包括长方体和圆柱体。

    （2）平行于底的平面被这个几何体所截的图形都与底相似，周长按离底的从近到远逐渐减少（线性较少）直到缩为一点，这样的几何体是锥体。锥体包括棱锥体和圆锥体。

    （3）用平行于底的平面截取锥体的一个小锥体，剩下的几何体就是台体。台体包括棱台体和圆台体。

八、几何体分类图

九、练习题

        把几何体、旋转体、多面体、柱体、锥体、台体、圆台、圆锥、圆柱、棱台、棱锥、正方体、长方体、直棱柱、棱柱填入下图适合位置：

附录：助记词

一对象，只形状，及空间，称为体。
大小别，形状异，数学里，理想化。

平面镜，所映体，与原体，轴对称。
任方向，移与旋，不重合，称手性。

平面镜，切两边，轴对称，轴对体。
该类体，无手性，该镜面，对称轴。

多边形，全包围，不凹陷，多面体。
这些形，体表面，形之边，体之棱。
六矩形，所围成，对面体，长方体。
若都是，正方形，称之为，正方体。

面平叠，是柱体，渐变点，是锥体。
一锥体，平截顶，所剩体，是台体。
多边形，作为底，是棱柱，或锥台。

一平面，绕一轴，转一周，旋转体。
若这轴，三角形，直角边，称圆锥。
若这轴，长方形，一条边，称圆柱。
若这轴，直角梯，垂直高，称圆台。
若这轴，离平面，旋转体，称环体。
若这面，是个圆，该环体，称圆环。
旋转体，轴对称，对称轴，无数个。

​